1 Worum geht es?

Gefragt ist nach Vierecken mit ganzzahligen Seitenlängen, bei denen auch beide Diagonalen ganzzahlige Längen haben.

Bei Quadraten ist das nicht möglich, da irrational.

2 Parallelogramme

Seitenlängen a und b mit und Diagonalenlängen e und f mit . Der Kosinussatz liefert die Bedingung:

Weiter muss:

Gesucht sind ganzzahlige Lösungen.

Beispiel:

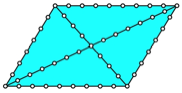
Beispiel

Liste:

a	b	e	f	Kommentar
4	3	5	5	Rechteck
5	5	8	6	Rhombus
7	4	9	7
7	6	11	7
9	7	14	8
9	8	13	11
10	5	13	9
11	7	14	12
11	8	17	9
11	10	19	9
12	5	13	13	Rechteck
12	11	19	13
13	6	17	11
13	9	20	10
13	11	18	16
13	13	24	10	Rhombus
14	13	21	17
15	8	17	17	Rechteck
15	10	19	17
15	10	23	11
16	7	21	13
16	11	23	15
16	13	25	15
16	13	27	11
16	15	29	11
17	6	19	17
17	9	22	16
17	11	26	12
17	14	23	21
17	16	27	19
17	17	30	16	Rhombus
18	11	23	19
18	13	25	19
19	8	25	15
19	9	22	20
19	12	29	13
19	13	24	22
19	17	30	20
19	17	34	12
19	18	29	23
20	15	31	17
20	17	33	17

Die Rechecke sind aus zwei pythagoreischen Dreiecken (Spiegelung an der Hypotenusenmitte) zusammengesetzt. Von den beiden Seitenlängen ist eine gerade und die andere ungerade. Die Diagonalenlänge ist ungerade.

Die Rhomben sind aus vier pythagoreischen Dreiecken (Spiegelungen an den Katheten) zusammengesetzt. Die Seitenlänge ist ungerade, beide Diagonalenlängen sind gerade.

3 Gleichschenklige Trapeze

Seiten a und c mit parallel, Schenkel b, Diagonale e. Satz des Ptolemäus (gleichschenklige Trapeze sind Sehnenvierecke) liefert die Bedingung:

Weiter muss gelten (kein „flaches“ Trapez) sowie .

Beispiel:

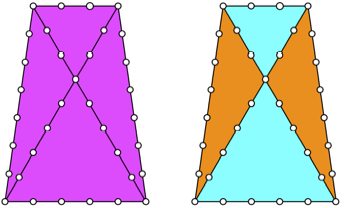
Beispiel

Das Beispiel ist aus pythagoreischen Dreiecken der 60°/120°-Geometrie zusammengesetzt.

Beispiel:

In diesem Beispiel ist der Diagonalenschnittpunkt kein Rasterpunkt auf den Diagonalen.

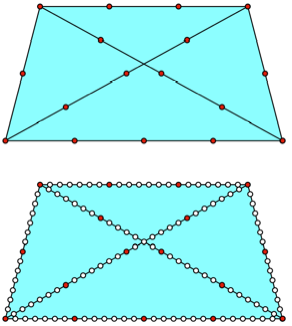
Beispiel

Wenn wir jedoch mit dem Faktor 7 aufblasen zu , erhalten wir einen Rasterpunkt als Diagonalenschnittpunkt. — Sind allgemein die Diagonalenschnittpunkte in diesem Sinne rational?

Liste:

a	b	c	e	Kommentar
3	4	3	5	Rechteck
4	2	3	4
4	3	4	5	Rechteck
5	7	3	8
5	4	4	6
5	12	5	13	Rechteck
6	5	4	7
7	10	3	11
7	6	4	8
7	17	5	18
8	5	3	7	Fibonacci-Trapez
8	7	4	9
8	3	5	7
8	9	5	11
8	11	6	13
8	5	7	9
8	13	7	15
8	15	8	17	Rechteck
9	13	3	14
9	8	4	10
9	6	5	9
9	9	7	12
9	3	8	9
9	7	8	11
9	17	8	19
10	9	4	11
10	19	8	21
11	16	3	17
11	10	4	12
11	9	8	13
11	15	9	18
12	8	3	10
12	11	4	13
12	14	5	16
12	7	6	11
12	17	6	19
12	4	7	10
12	20	7	22
12	5	8	11
12	7	10	13
12	13	10	17
12	8	11	14
12	5	12	13	Rechteck
13	19	3	20
13	12	4	14
13	11	8	15
13	18	9	21
13	10	12	16
14	13	4	15
14	11	12	17
14	19	12	23
15	14	4	16
15	11	5	14
15	8	7	13
15	16	7	19
15	7	8	13
15	13	8	17
15	11	9	16
15	14	11	19
15	4	12	14
15	17	13	22
15	8	15	17	Rechteck
16	11	3	13
16	15	4	17
16	8	5	12
16	19	5	21
16	12	7	16
16	5	9	13
16	9	9	15
16	16	9	20
16	7	11	15
16	20	11	24
16	13	12	19
16	9	13	17
16	4	15	16
16	7	15	17
16	11	15	19
16	17	15	23
17	16	4	18
17	15	8	19
17	14	12	20
17	13	16	21
18	17	4	19
18	9	8	15
19	18	4	20
19	17	8	21
19	16	12	22
19	15	16	23
20	14	3	16
20	19	4	21
20	13	6	17
20	12	9	18
20	6	11	16
20	7	12	17
20	11	12	19
20	17	12	23
20	8	13	18
20	9	14	19
20	11	16	21
20	12	17	22
20	9	18	21
20	13	18	23
20	14	19	24