Hans Walser, [20160807]
Geoblume
1 Abwicklung
Ist die Abwicklung der Geoblume (Abb. 1) korrekt?
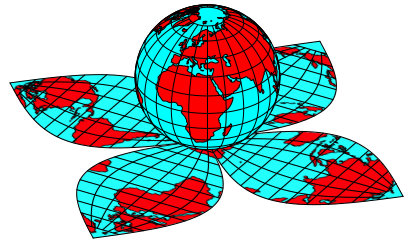
Abb. 1: Geoblume
2 Bearbeitung
Eine Kugel lŠsst sich nicht in den Ebene abwickeln. Die Abbildung 1 illustriert ein Artefakt.
Im Folgenden wird beschrieben wie die Figur zu verstehen ist.
2.1 Die Kugel
Die Erdkugel ist in orthografischer Projektion dargestellt. Sie ist gegenźber der Standarddarstellung um 30ˇ nach Westen verdreht. Die Erdachse ist um 30ˇ nach vorne gekippt. Der €quator erscheint daher als Ellipse mit dem AchsenverhŠltnis 2:1.
2.2 Die BlumenblŠtter
2.2.1 Sinusoidale Karten
Die vier BlumenblŠtter sind auf der Basis von sinusoidalen Karten (Mercator / Sanson) gezeichnet (Abb. 2). Sinusoidale Karten sind flŠchenverhŠltnistreu (equivalent). Die Mittelmeridiane sind der Reihe nach 0ˇE (Afrika und Europa), 90ˇE (Asien), 180ˇE (Pazifik), 270ˇE (Amerika).
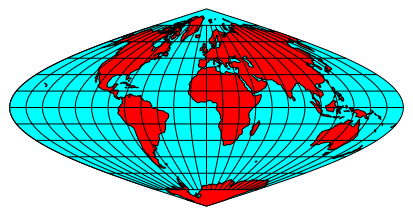
Abb. 2a: Afrika und Europa
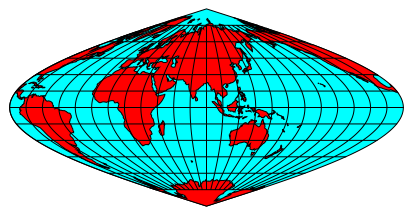
Abb. 2b: Asien
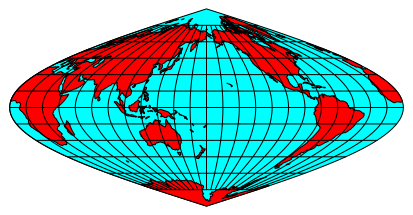
Abb. 2c: Pazifik
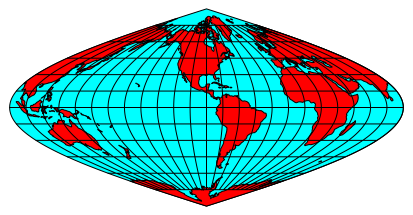
Abb. 2d: Amerika
2.2.2 Ausschnitte
Von jeder Karte nehmen wir den Ausschnitt zwischen den Meridianen, welche ±45ˇ vom Mittelmeridian abweichen (Abb. 3).
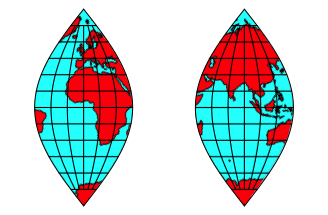
Abb. 3ab: Ausschnitte Afrika/Europa und Asien
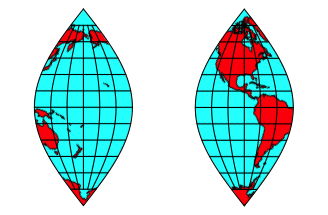
Abb. 3cd: Ausschnitte Pazifik und Amerika
2.3 Skalieren
Die
Ausschnitte der Abbildung 3 haben an den Spitzen keine rechten Winkel. Sie
lassen sich noch nicht bźndig zur Blume zusammensetzen. Wir erhalten die
rechten Winkel durch Skalieren in horizontaler Richtung mit dem Faktor 
(Abb. 4). Die
FlŠchenverhŠltnistreue bleibt bei dieser Skalierung erhalten.
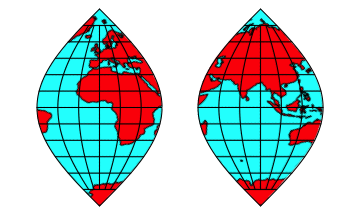
Abb. 4ab: Skaliert
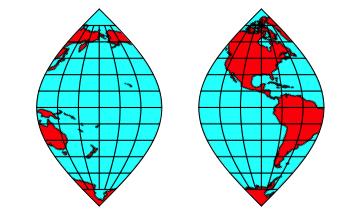
Abb. 4cd: Skaliert
2.4 Die Blume
Die BlŠtter der Abbildung 4 kšnnen mit dem Nordpol (Abb. 5) oder mit dem Sźdpol (Abb. 6) im Zentrum zusammengesetzt werden. Jede der beiden Blumen ist eine flŠchenverhŠltnistreue Karte (equivalent).
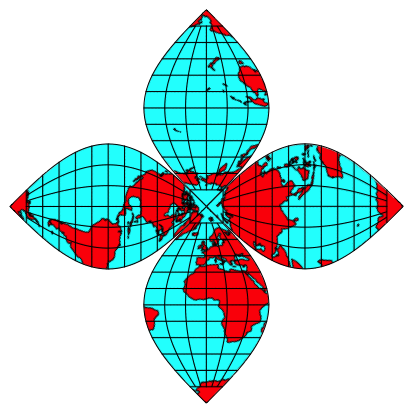
Abb. 5: Nordpol im Zentrum
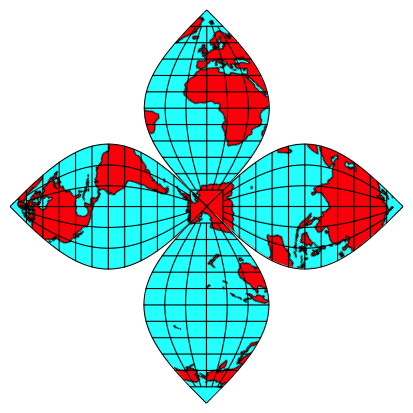
Abb. 6: Sźdpol im Zentrum
Fźr die Disposition der Abbildung 1 benštigen wir den Sźdpol im Zentrum.
3 Geoblume
Als Vorbereitung mźssen wir die Abbildung 6 spiegeln und gemŠ§ der Disposition der Kugel affin verzerren (Abb. 7).
Abb. 7: Spiegeln und Verzerren
Schlie§lich kšnnen wir die Kugel einsetzen (Abb. 1 und 8).
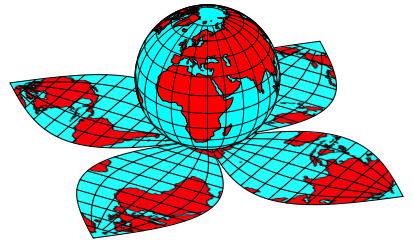
Abb. 8: Geoblume
Websites
Geodaten (07.08.2016)
http://swai.ethz.ch/swaie/MapProjector/MapProjector.de.html
Walser: Rund ohne ą (07.08.2016)
www.walser-h-m.ch/hans/Miniaturen/R/Rund_ohne_Pi/Rund_ohne_Pi.htm