Hans Walser, [20190312]
Geometrische Folge und Goldener Schnitt
Idee und Anregung: B. v. P.
1 Worum geht es?
Eine Dreiecksaufgabe mit einer geometrischen Folge fźhrt zum Goldenen Schnitt.
2 Das Problem
Gesucht
ist ein Dreieck, in welchem c, b, a, 
in
dieser Reihenfolge eine geometrische Folge bilden.
3 Bearbeitung
Wegen der Bedingung źber die geometrische Folge ist
(1)
mit einem noch unbekannte Quotienten q.
Fźr den FlŠcheninhalt A erhalten wir:
(2)
Die Seiten a und b stehen daher senkrecht. Wir haben ein rechtwinkliges Dreieck.
Aus dem Satz des Pythagoras
(3)
erhalten wir:
(4)
Diese biquadratische Gleichung fźr q hat die positive reelle Lšsung:
(5)
Dabei ist
der
Goldene Schnitt (Walser 2013).
Die Abbildung 1 zeigt das Dreieck.
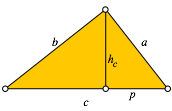
Abb. 1: Das Dreieck
4 Bemerkungen und ErgŠnzungen
á Der in der Abbildung 1 eingezeichnete Hypotenusenabschnitt p ist das nŠchste Glied der geometrischen Folge.
á Das Dreieck erscheint in anderem Kontext in Walser 2013, S. 173 und 189.
á Die geometrische Folge wird in [1] und [3] besprochen.
á Das Dreieck erscheint auch im Kontext der Kardioide, vgl. [1] und [2].
á Das Dreieck ist eines der wenigen Beispiele, in denen die Quadratwurzel aus dem Goldenen Schnitt erscheint.
Literatur
Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing źber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.
Weblinks
[1] Hans Walser: Means, Pythagoras and Golden Section
www.walser-h-m.ch/hans/Miniaturen/M/Means/Means.htm
[2] Hans Walser: Kardioide und Goldener Schnitt
www.walser-h-m.ch/hans/Miniaturen/K/Kardioide/Kardioide.htm
[3] Hans Walser: Geometric Sequence and Triangles
www.walser-h-m.ch/hans/Miniaturen/G/Geometric_Sequence/Geometric_Sequence.htm