Hans Walser, [20230710]

Geometrische Folge und Goldener Schnitt

1 Worum es geht

Geometrische Spielerei. Es erscheinen Quadratwurzeln aus dem Goldenen Schnitt.

2 Problemstellung

In einem Dreieck ABC bilden die drei Seiten a, b, c eine geometrische Folge mit dem Quotienten q.

3 Bearbeitung

Wir setzen a = 1, b = q und c = q². Die Ecken B und C halten wir fest, A variiert. Die Abbildung 1 zeigt die Situation.

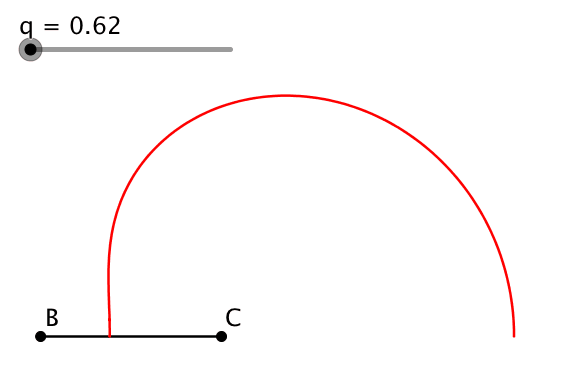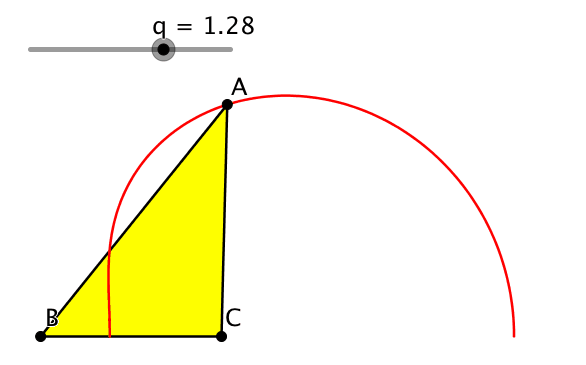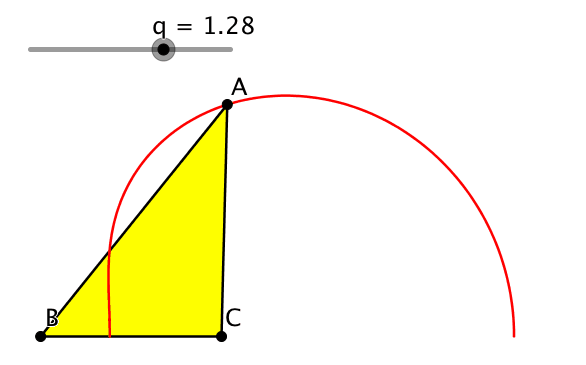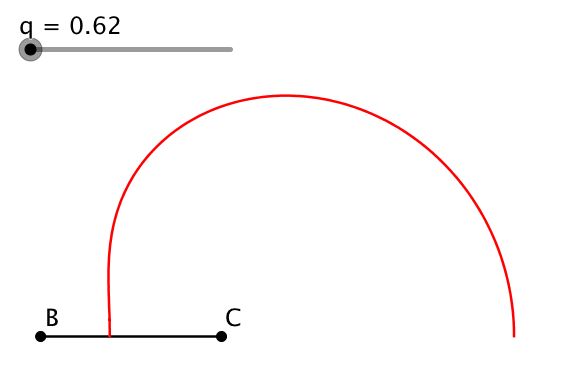
Abb. 1: Geometrische Folge der Dreieckseiten

4 Kommentare

4.1 Geometrisches Mittel

Die Seite b ist das geometrische Mittel der Seiten a und c.

4.2 Grenzen

Der Quotient q darf weder zu klein noch zu groß sein. Es gelten die Grenzen:

(–1+√5)/2 ≤ q ≤ (1+√5)/2

Die beiden Grenzen sind der kleine und der große Goldene Schnitt:

1/ Φ ≤ q ≤ Φ

Approximativ numerisch:

0.618 ≤ q ≤ 1.618

An den Grenzen sind die drei Punkte A, B und C kollinear.

4.3 Keine Spirale

Die Bahnkurve des Punktes A ist keine logarithmische Spirale. Ich wüsste auch gern, was für eine Kurve es ist.

4.4 Sonderfälle

Für q = √((–1+√5)/2) ≈ 0.786 ergibt sich ein rechtwinkliges Dreieck mit dem rechten Winkel in A (Abb. 2).

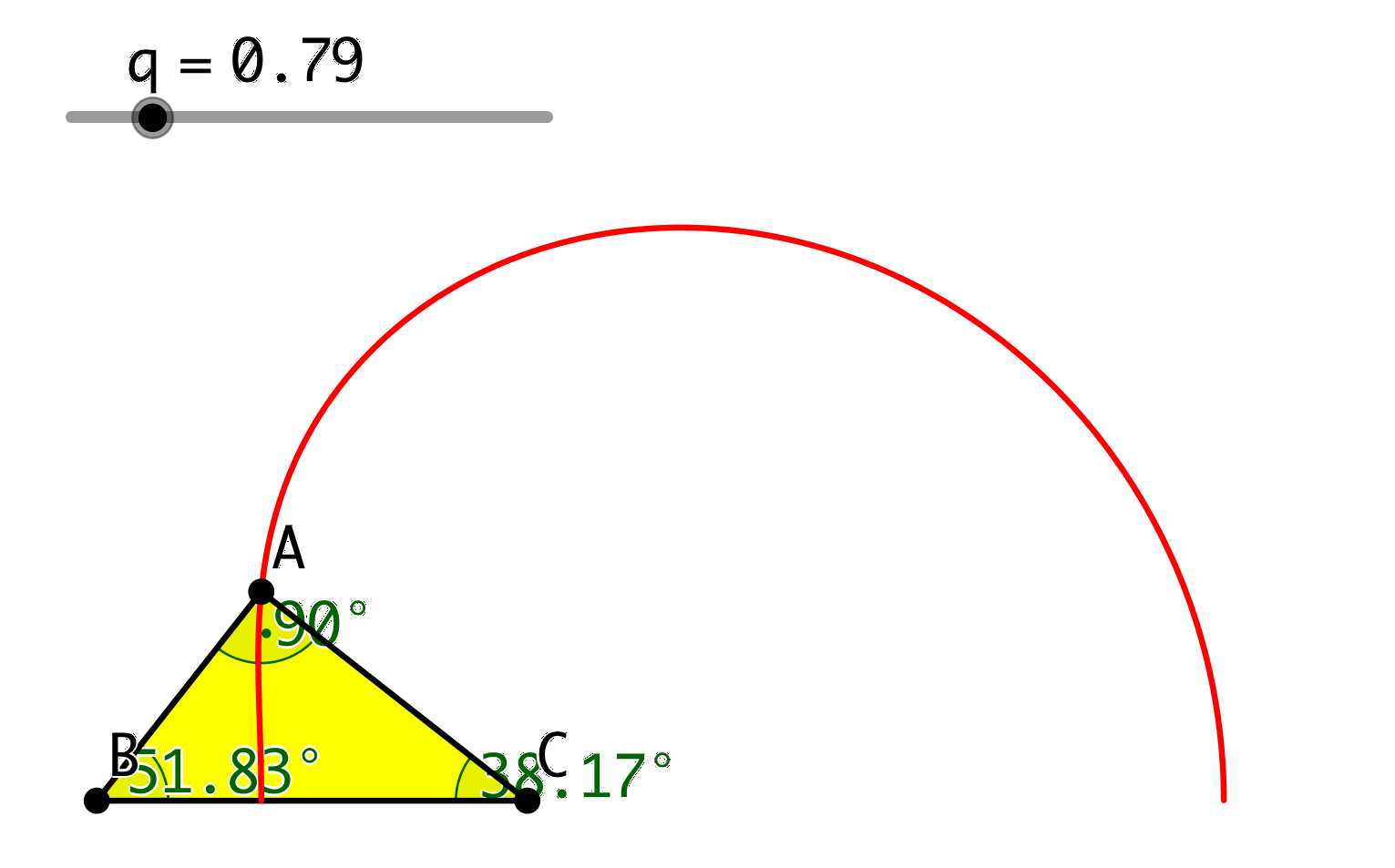
Abb. 2: Rechtwinkliges Dreieck

Für q= 1 ergibt sich das gleichseitige Dreieck (Abb. 3). Wer hätte das gedacht.

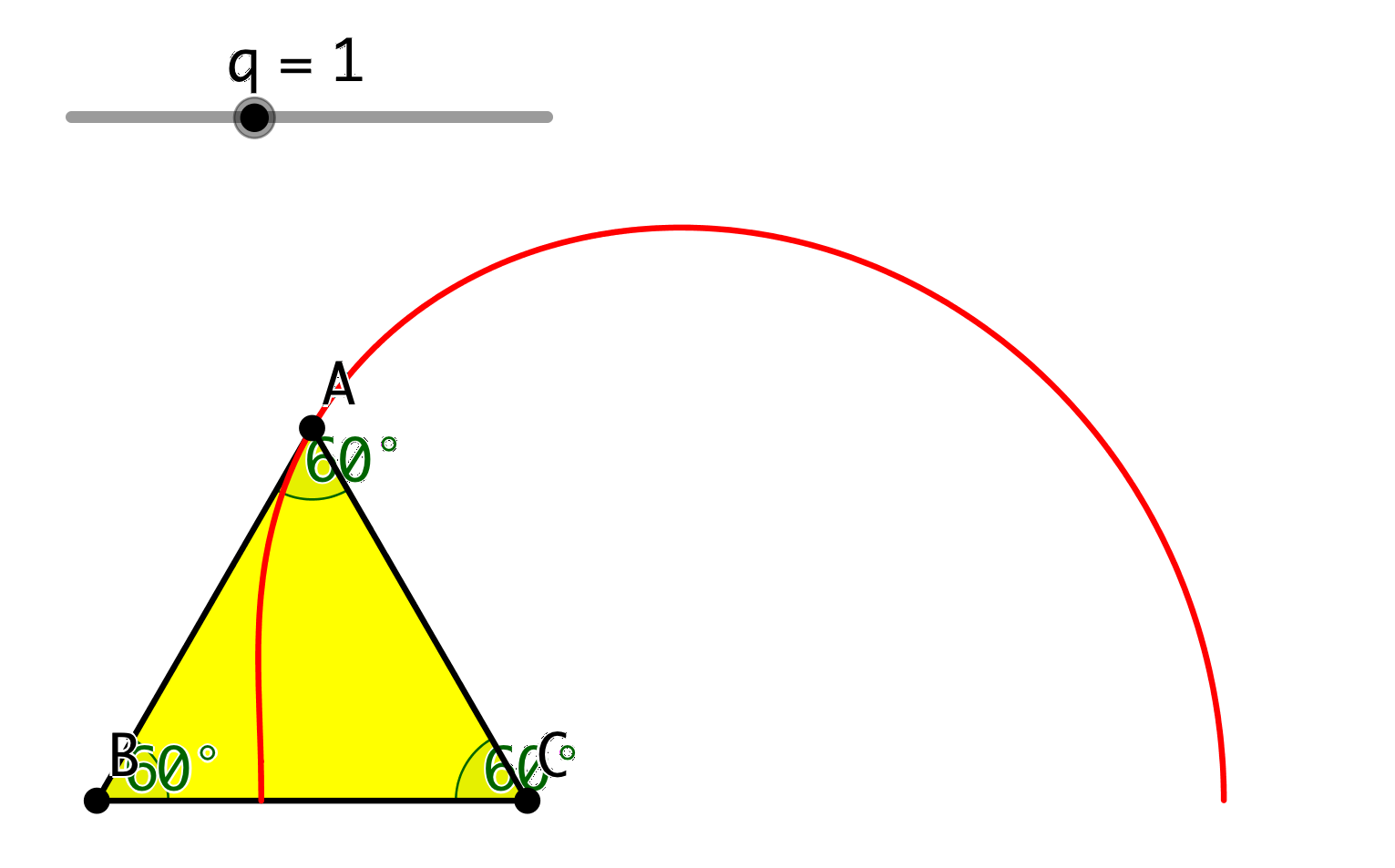
Abb. 3: Gleichseitiges Dreieck

Für q = √((1+√5)/2) ≈ 1.272 ergibt sich ein rechtwinkliges Dreieck mit dem rechten Winkel in C (Abb. 4). Die beiden rechtwinkligen Dreiecke (Abb. 2 und 4) sind ähnlich.

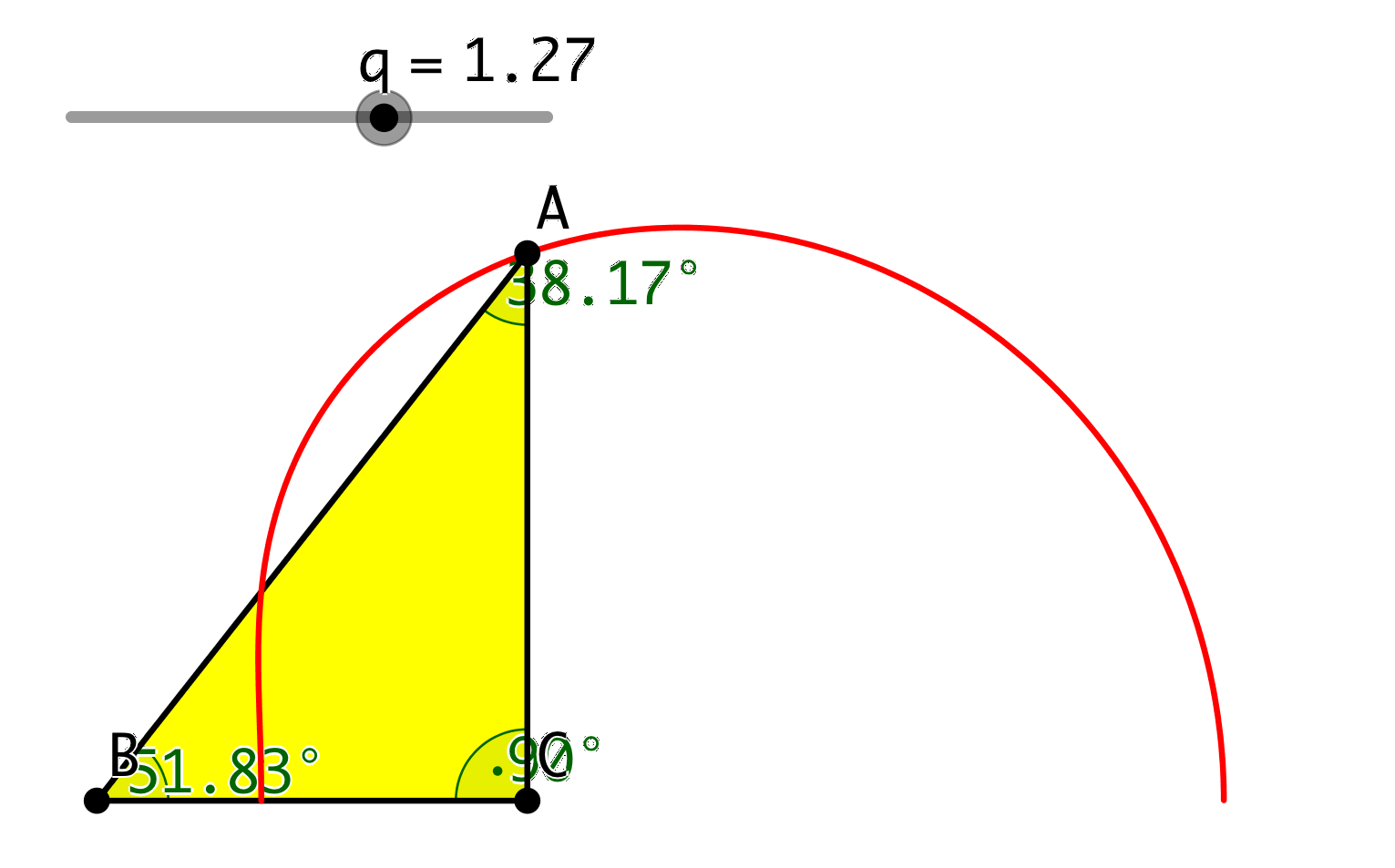
Abb. 4: Rechtwinkliges Dreieck

Weblinks

Hans Walser: Geometrische Folge und Goldener Schnitt

http://www.walser-h-m.ch/hans/Miniaturen/G/Geom_Folge/Geom_Folge.htm