Hans Walser, [20200201]
Geometrische Reihe
1 Worum geht es?
Illustration der geometrischen Reihe:
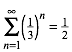(1)
2 Wurzel-3-Rechteck
Ein
Rechteck mit den SeitenlŠngen 1 und 
kann in
drei untereinander kongruente und zum Startrechteck Šhnliche Rechtecke
unterteilt werden (Abb. 1). Dabei muss vom Querformat auf Hochformat gewechselt
werden. Beweis rechnerisch.
Abb. 1: Wurzel-3-Rechteck
Wir machen nun daraus eine Trikolore (Abb. 2).
Abb. 2: Trikolore
Das rote und das blaue Rechteckt sind flŠchenmŠ§ig je ein Drittel des Startrechteckes.
Nun fŸgen
wir eine um den LŠngenfaktor 
verkleinerte und um 90¡ gedrehte Kopie
des Ganzen in die wei§e Mitte ein (Abb. 3).
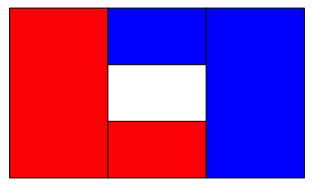
Abb. 3: Kopie einfŸgen
Das
zusŠtzliche rote Rechteck ist flŠchenmŠ§ig ein Neuntel des Startrechteckes. Der
Gesamte rote Anteil ist nun also 
des
Startrechteckes. Dasselbe gilt fŸr den gesamten blauen Anteil.
Wir kšnnen den Prozess wiederholen (Abb. 4).
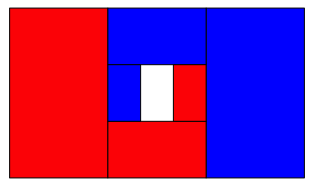
Abb. 4: Wiederholung des Prozesses
Der
gesamte rote Anteil ist nun 
. Wir haben die ersten drei Summanden der Reihe (1).
Iteration des Prozesses fŸhrt zu zwei ineinanderlaufenden Spiralen, welche das gesamte Startrechteck ausfŸllen (Abb. 5).
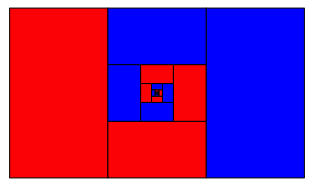
Abb. 5: Spiralen
Der gesamte rote Anteil ist nun die linke Seite von (1). Das gilt auch fŸr den gesamten blauen Anteil. Da das Startrechteck damit ausgefŸllt ist, ist der gesamte rote Anteil flŠchenmŠ§ig die HŠlfte des Startreckes. Damit gilt (1).
Die Animation 1 illustriert den Sachverhalt.
Animation 1: Ineinanderlaufende Spiralen
3 Sechseck
In ein regelmŠ§iges Sechseck zeichnen wir den Davidstern ein (Abb. 6).
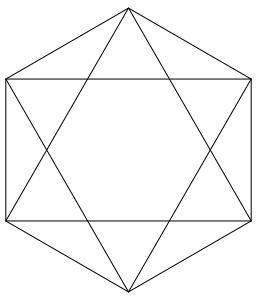
Abb. 6: Davidstern im Sechseck
Im Innern entsteht ein neues regelmŠ§iges Sechseck. Sein FlŠcheninhalt ist ein Drittel des FlŠcheninhaltes des Startsechseckes. Dies kann durch eine Triangulation (Abb. 7) eingesehen werden. Im zentralen Sechseck haben wir zwšlf von insgesamt 36 Dreiecken.
Abb. 7: Triangulation
Wir unterteilen nun die ZwischenflŠche zwischen den beiden Sechsecken in zwei kongruente Teile. Dies kann auf verschiedene Arten geschehen. Die Abbildung 8 zeigt ein Beispiel. Das rote und das blaue Teil sind je ein Drittel der FlŠche des Startsechseckes.
Abb. 8: Zwei kongruente Teile
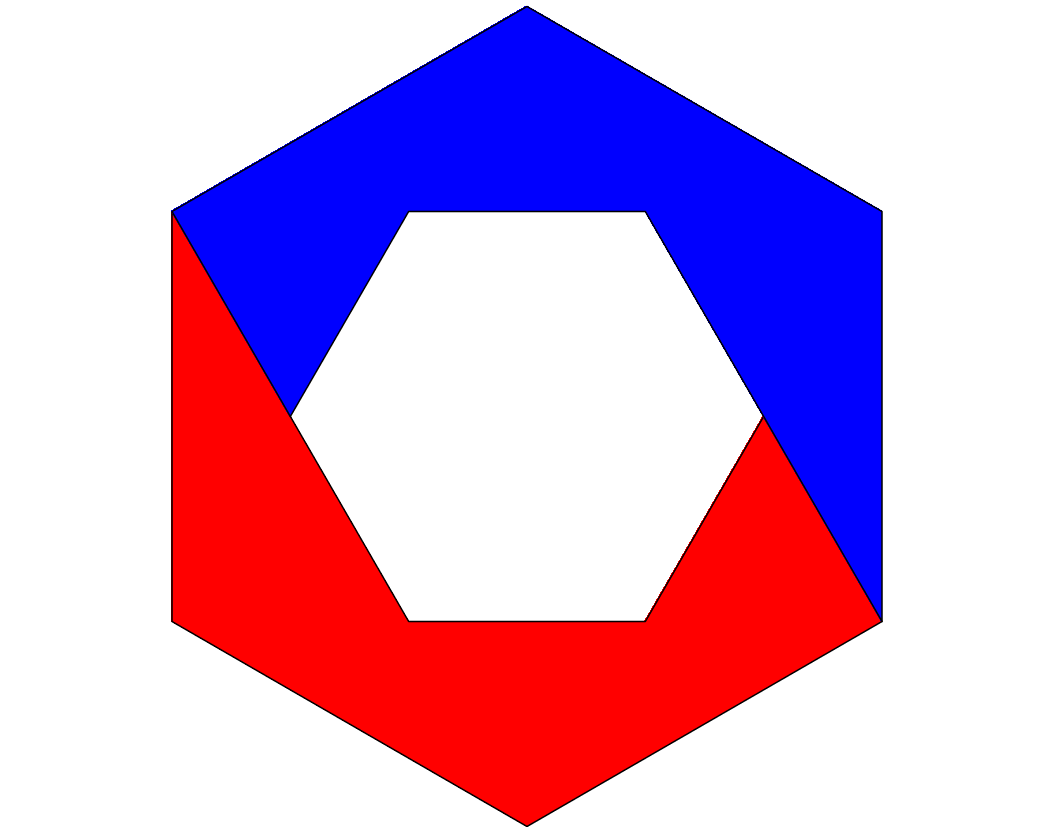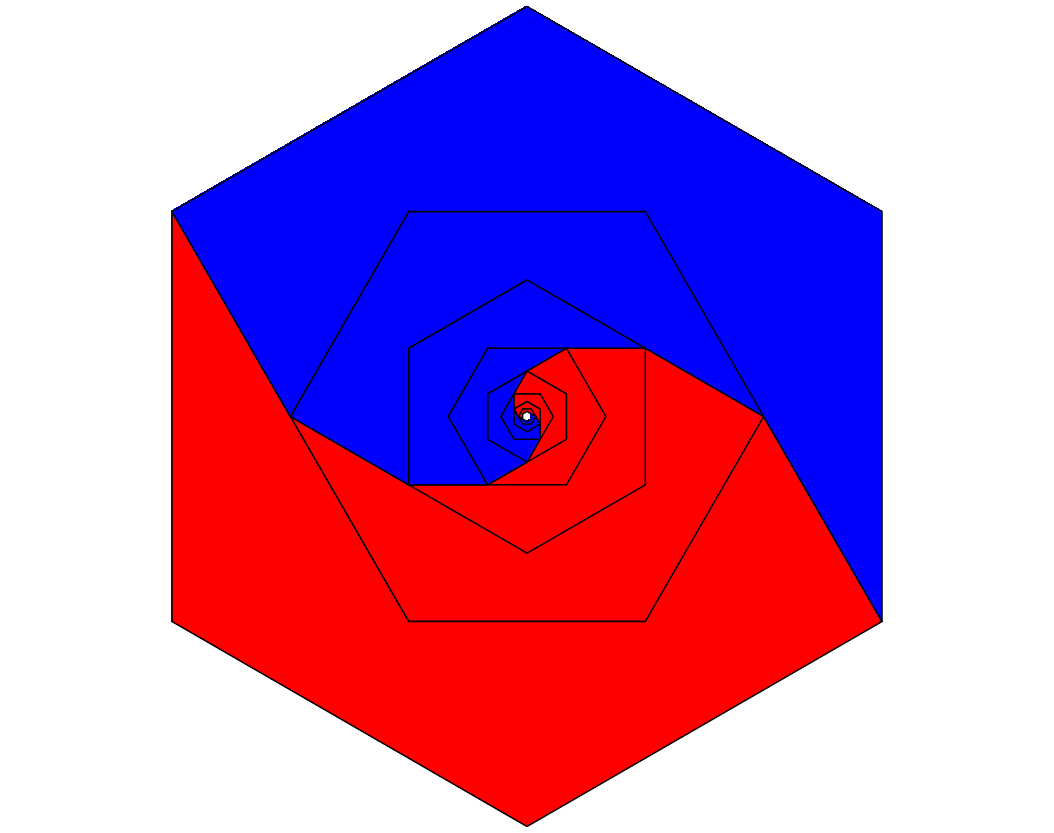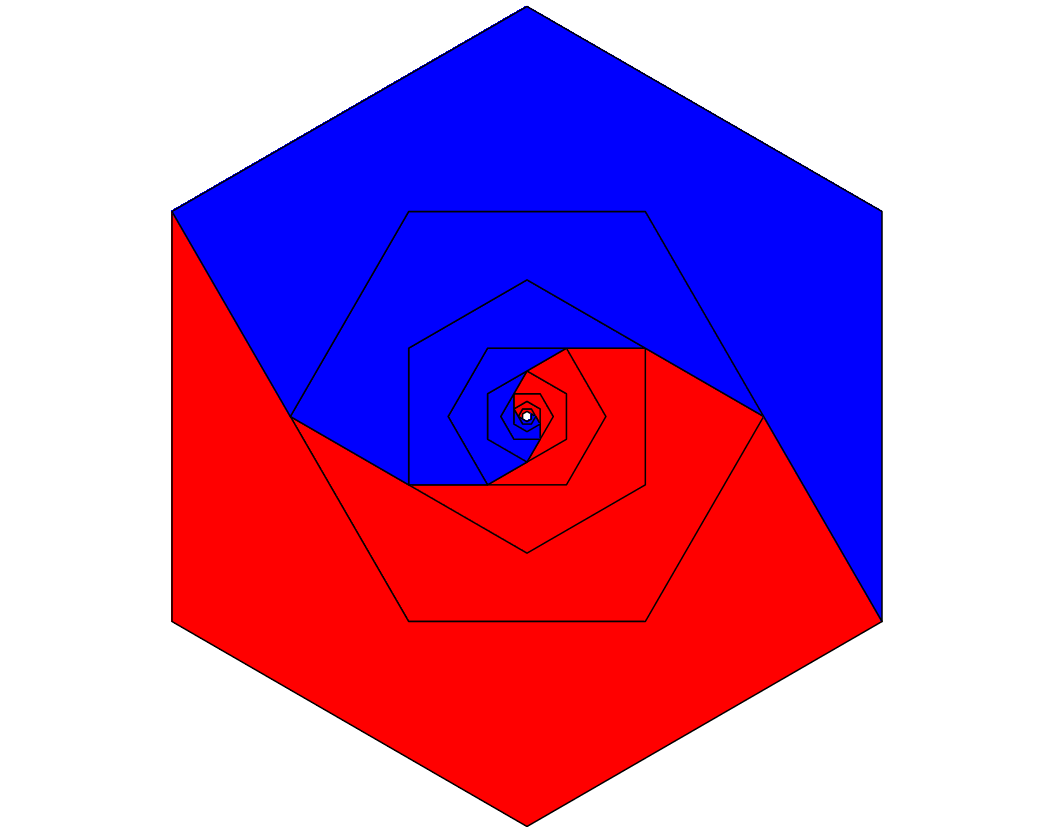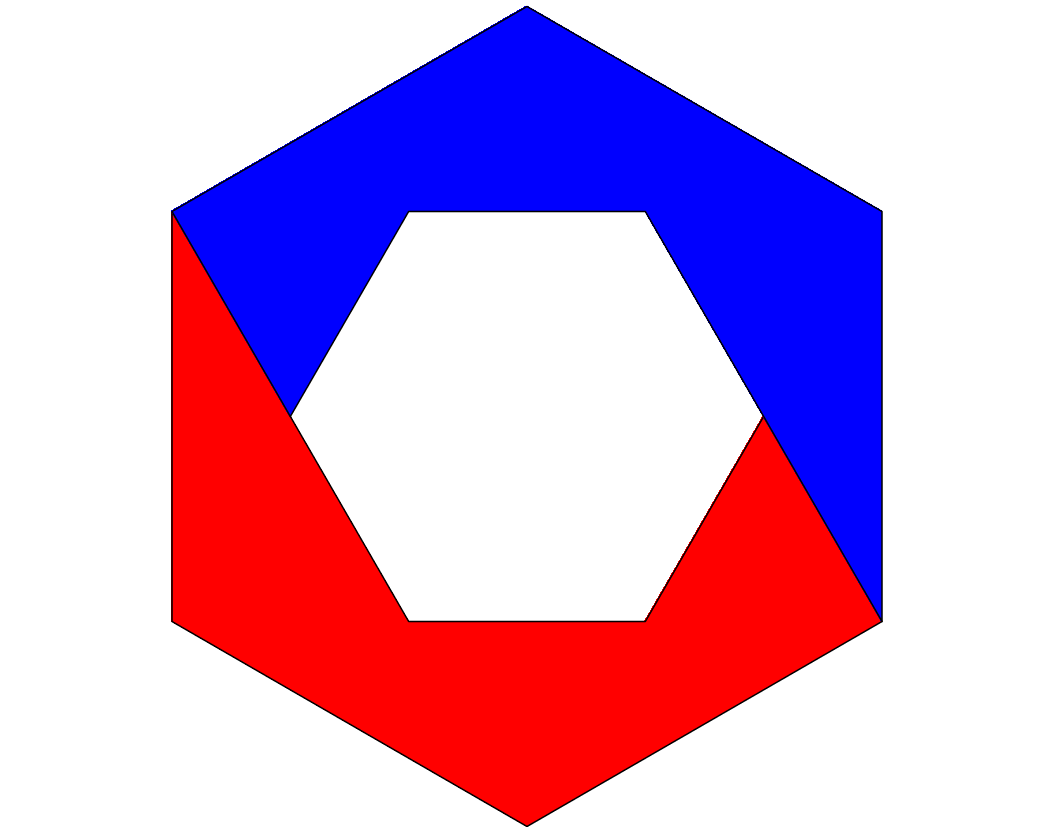
Und nun kšnnen wir eine flŠchenmŠ§ig auf einen Drittel verkleinerte Kopie in das wei§e Loch einsetzen (Abb. 9).
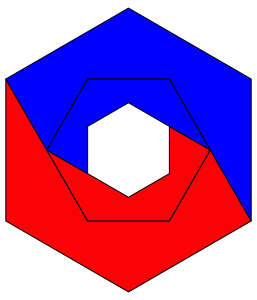
Abb. 9: Einsetzen einer Kopie
Der rote
Anteil an der FlŠche des Startsechseckes ist nun 
.
Nun iterieren wir den Prozess.
Die Abbildung 10 zeigt die Grenzsituation mit den beiden Spiralen.
Abb. 10: Spiralen
Die Animation 2 illustriert den Sachverhalt.
Animation 2: Ineinanderlaufende Spiralen
Bemerkung: Im Sechseck haben wir auch das Wurzel-3-Rechteck (Abb. 11). Sein FlŠcheninhalt ist zwei Drittel des FlŠcheninhaltes des Sechseckes.
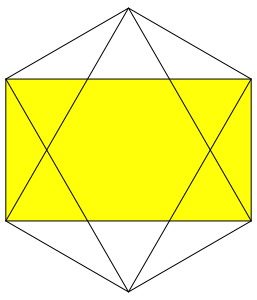
Abb. 11: Wurzel-3-Rechteck im Sechseck
4 Quadrat und Goldener Schnitt
Wir unterteilen ein Quadrat gemŠ§ Abbildung 12. Die drei eingezeichneten Punkte stehen im TeilverhŠltnis des Goldenen Schnittes (Walser 2013).
Das kleine Dreieck in der Mitte ist flŠchenmŠ§ig ein Drittel des Startquadrates. Beweis rechnerisch.
Abb. 12: Unterteilung mit dem Goldenen Schnitt
Wir fŸgen je zwei Au§endreiecke zu einem Bauteil zusammen (Abb. 13). Deren FlŠche ist je gleich gro§ wie jene des kleinen Quadrates.
Abb. 13: Zwei Teile
Nun fŸgen
wir eine um den LŠngenfaktor 
verkleinerte und passend gedrehte Kopie
des Ganzen in die wei§e Mitte ein (Abb. 14). Wir erhalten den Beginn von Spiralen.
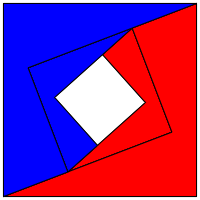
Abb. 14: Beginn der Spiralen
Die Abbildung 15 zeigt die beiden Spiralen und damit erneut eine Illustration von (1).
Abb. 15: Spiralen
Die Animation 3 illustriert den Sachverhalt.
Animation 3: Ineinanderlaufende Spiralen
Websites
Hans Walser: Dodekagramm und Triakontagramme
http://www.walser-h-m.ch/hans/Miniaturen/D/Dodekagramm/Dodekagramm.htm
Literatur
Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing Ÿber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.