Hans Walser, [20200203]

Geometrische Reihe

1   Worum geht es?

Illustrationen der geometrischen Reihe:

 

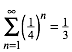                                                                                                                 (1)

 

2   Rechteck

Das Wurzel-4-Rechteck ist das Rechteck mit dem SeitenverhŠltnis 2:1 (Abb. 1). Wir kšnnen es in vier kongruente, zum Startrechteck Šhnliche Rechtecke unterteilen. Dabei muss von Querformat auf Hochformat gewechselt werden.

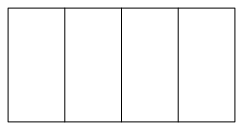
Abb. 1: Wurzel-4-Rechteck

Wir fŠrben nun drei der vier Rechtecke, und lassen das vierte leer (Abb. 2).

Abb. 2: FŠrbung

Das leere Feld fŸllen wir mit einer lŠngenmŠ§ig auf 50% verkleinerten und um +90¡ gedrehten Kopie der Gesamtfigur (Abb. 3).

Abb. 3: Erster Schritt

Diesen Schritt wiederholen wir (Abb. 4).

Abb. 4: Zweiter Schritt

Schlie§lich ist das ganze Startrechteck ausgefŸllt (Abb. 5).

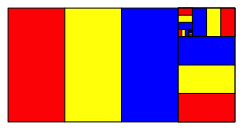
Abb. 5: Grenzfigur

Fokussierung auf zum Beispiel die roten Rechtecke illustriert (1).

Die Abbildung 6 zeigt eine Variante der Farbanordnung. Wir erkennen zumindest eine Spirale.

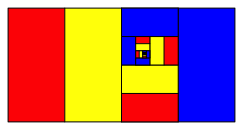
Abb. 6: Variante

3   Quadrat

Die Abbildungen 7 bis 10 zeigen einen Klassiker. Wir vierteln ein Quadrat gemŠ§ Abbildung 7 und fŸllen drei der vier Viertel mit Farbe (Abb. 8).

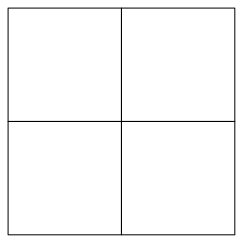
Abb. 7: Vierteln des Quadrates

Abb. 8: Drei Viertel gefŠrbt

Das leere Feld fŸllen wir mit einer lŠngenmŠ§ig auf 50% verkleinerten Kopie der Gesamtfigur (Abb. 9).

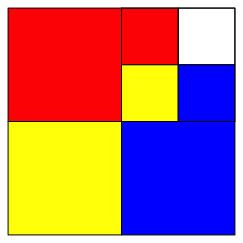
Abb. 9: Erster Schritt

Iteration fŸhrt zum Klassiker der Abbildung 10. Der Grenzpunkt ist rechts oben.

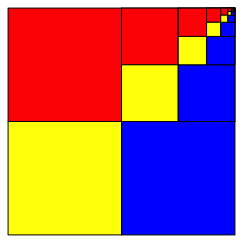
Abb. 10: Klassiker

Wenn wir nicht nur verkleinern, sondern bei jedem Schritt auch um +90¡ drehen, ergibt sich die Variante der Abbildung 11. Wir erkennen zumindest eine Spirale. Wo ist der Grenzpunkt?

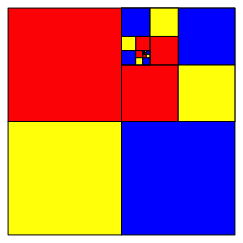
Abb. 11: Variante

Wenn wir bei jedem Schritt um 180¡ drehen, ergibt sich die Variante der Abbildung 12. Hier ist die Position des Grenzpunktes leicht zu bestimmen. Wenn wir von rechts und von oben her arbeiten, kommen wir wiederum zu (1), diesmal lŠngenmŠ§ig.

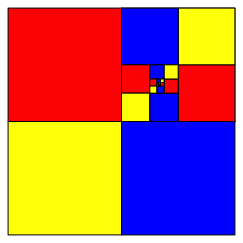
Abb. 12: Noch eine Variante

Durch geeignete Organisation der Verteilung kann jeder Punkt im inneren und auf dem Rand des Startquadrates als Grenzpunkt erhalten werden (Algorithmus der Katze, die um den hei§en Brei schleicht).

4   Dreieck

4.1  Klassische Unterteilung

Wir beginnen mit der klassischen Unterteilung gemŠ§ Abbildung 13.

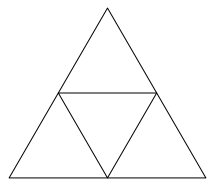
Abb. 13: Klassische Unterteilung

Mit der FŠrbung der Abbildung 14 ergibt sich schlie§lich die Figur der Abbildung 15. Diese erinnert an die Abbildung 10.

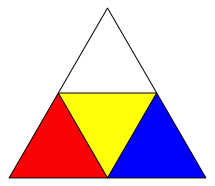
Abb. 14: FŠrbung

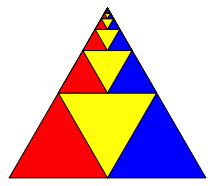
Abb. 15: Grenzfigur

Mit der FŠrbung gemŠ§ Abbildung 16 kšnnen wir drei ineinanderlaufende Spiralen konstruieren (Abb. 17).

Abb. 16: Andere FŠrbung

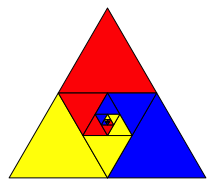
Abb. 17: Spiralen

Mit der FŠrbung der Abbildung 16 kšnnen wir aber auch anders verfahren (Abb. 18). Jede Farbe hat nun ihre Symmetrieachse.

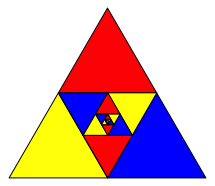
Abb. 18: Variante

4.2  Rasterung

Wir versehen das Dreieck mit einer 6×6-Rasterung (Abb. 19). Im rot markierten zentralen Dreieck befinden sich neun der insgesamt 36 Rasterdreiecke, ein Viertel also.

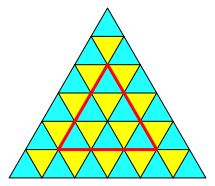
Abb. 19: Rasterung

Die ZwischenflŠche zwischen dem roten Dreieck und dem Startdreieck zerlegen wir in drei flŠchengleiche Teile (Abb. 20). Diese haben ebenfalls je neun Rasterdreiecke.

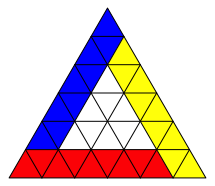
Abb. 20: FlŠchengleiche Teile

Im Folgenden lassen wir die Rasterdreiecke weg. Das leere zentrale Dreieck fŸllen wir mit einer lŠngenmŠ§ig auf 50% verkleinerten und um +120¡ gedrehten Kopie der Gesamtfigur (Abb. 21). Wir sehen den Beginn von drei Spiralen.

Abb. 21: Erster Schritt

Die Abbildung 22 zeigt die Grenzfigur.

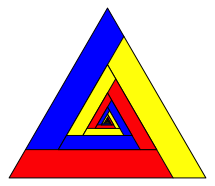
Abb. 22: Spiralen

4.3  Goldener Schnitt

Wir zerlegen das Dreieck gemŠ§ Abbildung 23. Die drei markierten Punkte liegen im VerhŠltnis des Goldenen Schnittes (Walser 2013). Das zentrale gleichseitige Dreieck ist flŠchenmŠ§ig ein Viertel des Startdreieckes. Beweis rechnerisch.

Abb. 23: Zerlegung mit dem Goldenen Schnitt

Die Au§endreiecke sind flŠchenmŠ§ig gleich gro§ wie das zentrale Dreieck. Wir fŠrben die drei Au§endreiecke (Abb. 24).

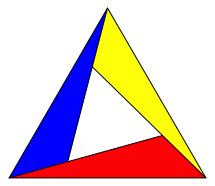
Abb. 24: FŠrbung

Das leere zentrale Dreieck fŸllen wir mit einer lŠngenmŠ§ig auf 50% verkleinerten und geeignet gedrehten Kopie der Gesamtfigur (Abb. 25). Wir sehen den Beginn von drei Spiralen.

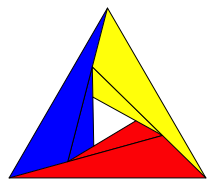
Abb. 25: Erster Schritt

Die Abbildung 26 zeigt die Grenzfigur.

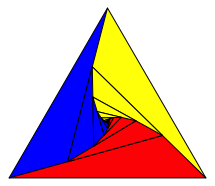
Abb. 26: Grenzfigur

Websites

Hans Walser: Geometrische Reihe

http://www.walser-h-m.ch/hans/Miniaturen/G/Geom_Reihe2/Geom_Reihe2.htm

 

 

Literatur

Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing Ÿber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.