Hans Walser, [20200204]
Geometrische Reihe
1 Worum geht es
Visualisierung der geometrischen Reihe
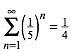(1)
2 Wurzel-5-Rechteck
Das
Wurzel-5-Rechteck ist das Rechteck mit dem SeitenverhŠltnis 
(Abb. 1).
Wir kšnnen es in fŸnf kongruente, zum Startrechteck Šhnliche Rechtecke
unterteilen. Dabei muss von Querformat auf Hochformat gewechselt werden.
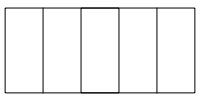
Abb. 1: Wurzel-5-Rechteck
Wir fŠrben nun vier der fŸnf Rechtecke, und lassen eines leer (Abb. 2).
Abb. 2: FŠrbung
Das leere
Feld fŸllen wir mit einer lŠngenmŠ§ig um den Faktor 
verkleinerten
und um +90¡ gedrehten Kopie der Gesamtfigur (Abb. 3).
Abb. 3: Erster Schritt
Diesen Schritt wiederholen wir (Abb. 4).
Abb. 4: Zweiter Schritt
Schlie§lich ist das ganze Startrechteck ausgefŸllt (Abb. 5).
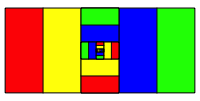
Abb. 5: Grenzfigur
3 Klassiker
Wir zerlegen ein Quadrat gemŠ§ Abbildung 6.
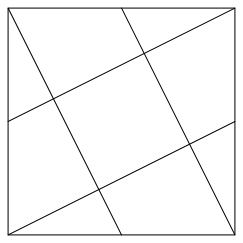
Abb. 6: Zerlegung
Das kleine zentrale Quadrat ist flŠchenmŠ§ig ein FŸnftel des Startquadrates. Die Abbildung 7 zeigt einen Zerlegungsbeweis dazu.
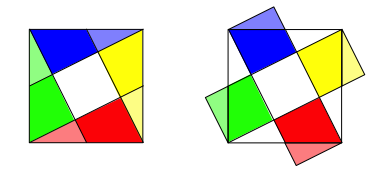
Abb. 7: Zerlegungsbeweis
Wir fŠrben vier Au§enteile gemŠ§ der Zerlegung der Abbildung 6 (Abb. 8).
Abb. 8: FŠrbung
Das leere
zentrale Quadrat fŸllen wir mit einer lŠngenmŠ§ig um den Faktor 
verkleinerten und geeignet gedrehten
Kopie der Gesamtfigur (Abb. 9). Wir sehen den Beginn von vier Spiralen.
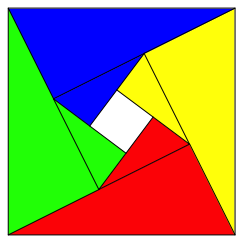
Abb. 9: Erster Schritt
Die Abbildung 10 zeigt die Grenzfigur.
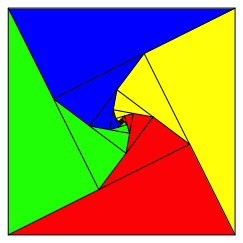
Abb. 10: Grenzfigur
Die Animation 1 illustriert den Sachverhalt.
Animation 1: Klassiker
4 Goldener Schnitt
Wir unterteilen das Quadrat gemŠ§ Abbildung 11. Die drei markierten Punkte liegen im TeilverhŠltnis des Goldenen Schnittes (Walser 2013).
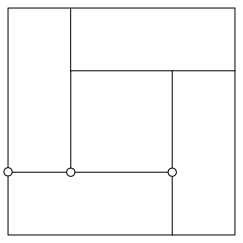
Abb. 11: Unterteilung mit dem Goldenen Schnitt
Das zentrale Quadrat ist flŠchenmŠ§ig ein FŸnftel des Startquadrates. Beweis rechnerisch mit dem Goldenen Schnitt oder durch eine Zerlegung (Abb. 12).
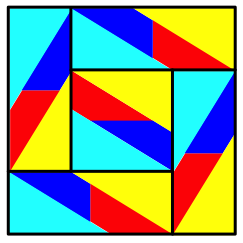
Abb. 12: Zerlegungsbeweis
Wir fŠrben vier Au§enrechtecke der Abbildung 11 gemŠ§ Abbildung 13.
Abb. 13: FŠrbung
Das leere
zentrale Quadrat fŸllen wir mit einer lŠngenmŠ§ig um den Faktor 
verkleinerten und um +90¡ gedrehten Kopie
der Gesamtfigur (Abb. 14). Wir sehen den Beginn von vier Spiralen.
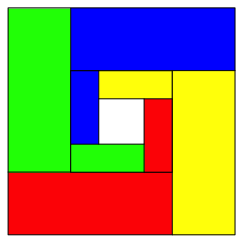
Abb. 14: Erster Schritt
Die Abbildung 15 zeigt die Grenzfigur.
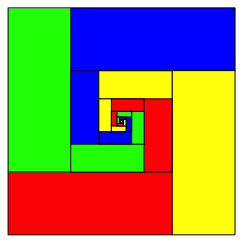
Abb. 15: Grenzfigur
5 Handgestrickt
Die Abbildung 16 zeigt eine recht willkŸrliche Unterteilung. Das zentrale Quadrat ist lŠngenmŠ§ig ein FŸnftel des Startquadrates. Dies wurde einfach so gemacht.
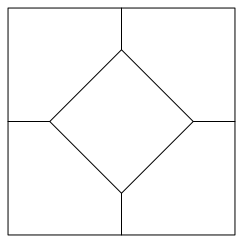
Abb. 16: WillkŸrliche Unterteilung
Wir fŠrben vier Au§enrechtecke der Abbildung 16 gemŠ§ Abbildung 17.
Abb. 17: FŠrbung
Das leere
zentrale Quadrat fŸllen wir mit einer lŠngenmŠ§ig um den Faktor 
verkleinerten und um +45¡ gedrehten Kopie
der Gesamtfigur (Abb. 18). Wir sehen den Beginn von vier Spiralen.
Abb. 18: Erster Schritt
Die Abbildung 19 zeigt die Grenzfigur.
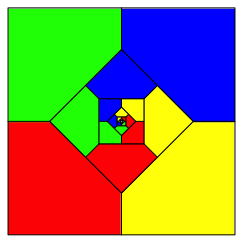
Abb. 19: Grenzfigur
Websites
Hans Walser: Geometrische Reihe
http://www.walser-h-m.ch/hans/Miniaturen/G/Geom_Reihe2/Geom_Reihe2.htm
Hans Walser: Geometrische Reihe
http://www.walser-h-m.ch/hans/Miniaturen/G/Geom_Reihe3/Geom_Reihe3.htm
Literatur
Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing Ÿber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.