Hans Walser, [20110925a]
Gleichdick
Anregung: J. R., K.-L.
Es werden Gleichdicke aus Kreissektoren aufgebaut. Ein Grenzbergang fhrt zu Gleichdicken, die aus Kreisevolventen zusammengesetzt sind.
1 Konstruktion
In die Au§enwinkel eines gleichseitigen Dreieckes passen wir regelm§ige Zwlfecke ein.
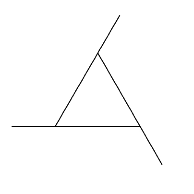
Dreieck mit Zwlfecken
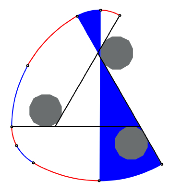
Nun zeichnen wir 30¡-Sektoren ein gem§ Abbildung. Die Zentren der Sektoren liegen auf Eckpunkten des oberen Zwlfeckes. Der Radius des ersten Sektors ist frei whlbar, der Radius des zweiten Sektors muss passend gewhlt werden, so dass wir einen glatten bergang bei den Sektorbgen erhalten. Er ist die Summe des Radius des ersten Sektors plus der Seitenlnge des Zwlfeckes.
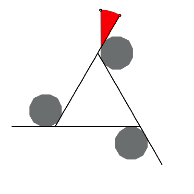
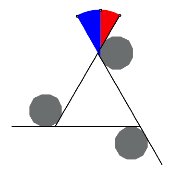
Erster und zweiter Sektor
Nun zeichnen wir den dritten und den vierten 30¡-Sektor. Die Zentren sind Eckpunkte des Zwlfeckes rechts unten. Die Radien werden so gewhlt, dass glatte bergnge entstehen.
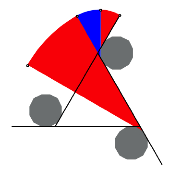
Dritter und vierter Sektor
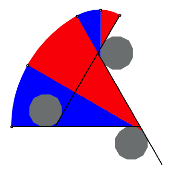
Der fnfte und sechste Sektor ist je gleich gro§ wie der erste und zweite Sektor. Dies kann so gezeigt werden. Wir bezeichnen die Seitenlnge des gleichseitigen Dreiecks mit d, die Seitenlnge des Zwlfeckes mit z und den Radius des ersten roten Sektors mit r. Es ist dann:

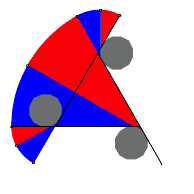
Weitere Sektoren
Weiter gilt fr Gegensektoren:
![]()
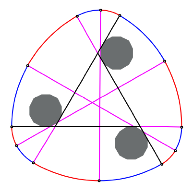
Wir
erhalten eine Figur, welche berall den gleichen Durchmesser ![]() hat, ein
Gleichdick also.
hat, ein
Gleichdick also.
Das Gleichdick hat zwar eine dreistrahlige Drehsymmetrie, aber keine Symmetrieachsen.
2 Variationen
Bei gegebenem Startdreieck, also gegebenem d, knnen wir noch die Gr§e der Zwlfecke (also z) und den Radius r des ersten Sektors variieren.
Im folgenden einige Bilder.
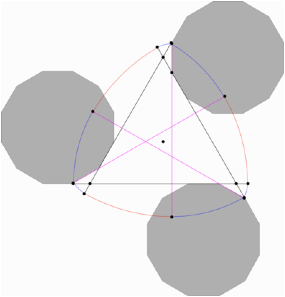
![]()
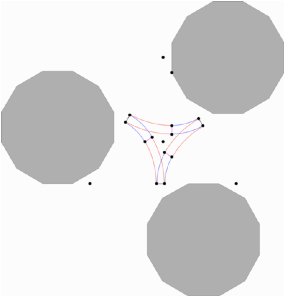
Mbiusband,
![]()
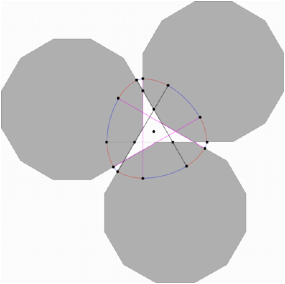
Achsensymmetrie
3 Ausblicke
Statt mit
Zwlfecken knnen wir auch mit 18-Ecken, 24-Ecken, 30-Ecken etc. arbeiten, also
allgemein mit ![]() .
.
Wenn wir
mit Sechsecken arbeiten, erhalten wir fr ![]() das gewhnliche
und fr beliebiges r das
verallgemeinerte Reuleaux-Dreieck.
das gewhnliche
und fr beliebiges r das
verallgemeinerte Reuleaux-Dreieck.
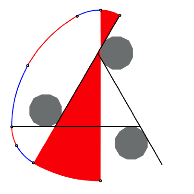
Fr ![]() ergibt sich ein
Gleichdick, das aus Kreisevolventen zusammengesetzt ist. Die folgende Abbildung
zeigt ein Beispiel, dabei sind die Evolventenbgen auf den ersten Blick kaum
von Kreisbgen unterscheidbar.
ergibt sich ein
Gleichdick, das aus Kreisevolventen zusammengesetzt ist. Die folgende Abbildung
zeigt ein Beispiel, dabei sind die Evolventenbgen auf den ersten Blick kaum
von Kreisbgen unterscheidbar.
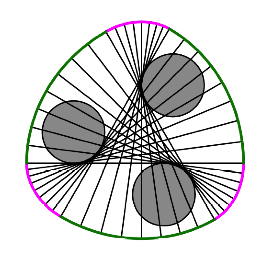
Gleichdick aus Kreisevolventen
Im folgenden Beispiel wird die Asymmetrie der Evolventenbgen besser sichtbar.
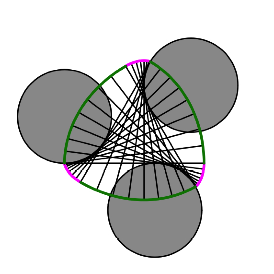
Deutliche Evolventenbgen