Hans Walser, [20111008a]
Gleichdick auf der Basis einer Zykloide
Es wird ein Sonderfall
eines Gleichdicks besprochen, das durch AbwŠlzen einer Strecke auf einer
Zykloide entsteht.
1
Die Zykloide
Parameterdarstellung:
Der Faktor 
ist lediglich
eine Skalierungsfaktor und geometrisch unwesentlich. Die Zykloide entsteht
durch Hinaufrollen eines Kreises mit Radius 
auf der Geraden 
.
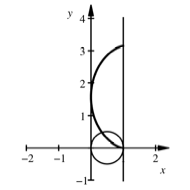
Zykloide
2
BogenlŠnge
Die Zykloide hat die
Spannweite 
und die
BogenlŠnge 4. Dies kann wie folgt eingesehen werden: Die Spannweite entspricht
dem Umfang des Rollkreises. Fźr die BogenlŠnge eine kleine Rechnung:
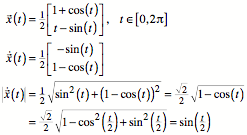
Fźr die BogenlŠnge 
erhalten wir
daraus:
Somit ist 
.
3
Dreispitz
Wir nehmen nun nur die
untere HŠlfte der Zykloide und spiegeln an der y-Achse. Schlie§lich ergŠnzen wir mit der Strecke von 
nach 
.
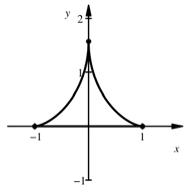
Dreispitz
Wir erhalten so einen
gleichseitigen Dreispitz mit den Ecken A, B
und 
. Die SeitenlŠnge ist 2.
4
Gleichdick
Nun wŠlzen wir eine
Strecke der LŠnge 2 zunŠchst auf dem rechten und dann auf dem linken
Zykloidenbogen ab.
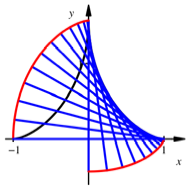
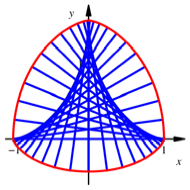
AbwŠlzen einer Strecke
Wir erhalten ein
Gleichdick mit dem Durchmesser 2 und dem Umfang 
(wie der Einheitskreis,
daher der Skalierungsfaktor 
bei der
anfŠnglichen Zykloide).
5
Abstandslinien
Mit Hilfe von
Abstandslinien erhalten wir weitere Gleichdicke.
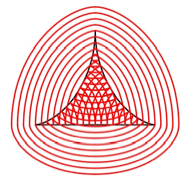
Abstandslinien