Hans Walser, [20160531]

Gleiche Sehnen

Idee und Anregung: W. K., F.

1 Problem

Zu zwei Kreisen k₁(M₁, r₁) und k₂(M₂, r₂) soll eine Gerade g durch einen gegebenen Punkt P gefunden werden, welche aus den beiden Kreisen gleich lange Sehnen herausschneidet (Abb. 1).

Abb. 1: Gleich lange Sehnen

2 Experimentelle Lösung

2.1 Propeller

Wir zeichnen von P aus einen Strahl, welcher den Kreis k₂ schneidet, und tragen die Sehnenlänge von P aus auf dem Strahl ab (Abb. 2).

Abb. 2: Sehnenlänge

So entsteht eine Kurve mit einer Spitze. Aus Liebe zur Symmetrie spiegeln wie sie an P. Damit erhalten wir einen Propeller (Abb. 3).

Abb. 3: Propeller

2.2 Schnitt zweier Propeller

Wir zeichnen nun für beide Kreise je den Propeller (Abb. 4). Die gesuchte Gerade geht durch deren Schnittpunkt. In unserem Beispiel gibt es zwei Lösungen.

Abb. 4: Lösungen

3 Zirkel und Lineal

3.1 Potenzgerade

Mit S bezeichnen wir die Mitte zwischen den zwei gleich langen Sehnen (Abb. 5). Der Punkt S hat gegenüber beiden Kreisen die gleiche Potenz, er liegt also auf der Potenzgeraden h der beiden Kreise.

Abb. 5: Potenzgerade

3.2 Mittelparallele

Die Normale in S auf die Gerade g ist Mittelparallele der beiden Mittelsenkrechten der gleich langen Sehnen (Abb. 6). Diese Normale verläuft also auch durch den Mittelpunkt O der Strecke M₁M₂ (Strahlensätze). Daher liegt der Punkt S auf dem Thaleskreis t über der Strecke OP.

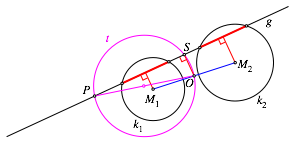
Abb. 6: Mittelparallele und Thaleskreis

3.3 Lösung

Wir finden S also als Schnittpunkt der Potenzgeraden h mit dem Thaleskreis t (Abb. 7). Damit kann g gezeichnet werden. In unserem Beispiel gibt es zwei Lösungen.

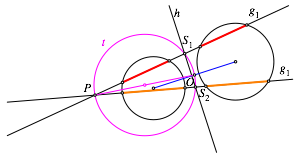
Abb. 7: Lösung

4 Problemvariante

Gesucht ist eine Gerade g, welche aus beiden Kreisen gleich lange Sehnen herausschneidet und zu einer gegebenen Geraden p parallel ist.

Die Lösung sei der geneigten Leserin überlassen.