Hans Walser, [20160537]
Gleiche Sehnen
Anregung: W. K., F.
1 Worum geht es?
Gegeben seien drei Kreise ki(Mi, ri), i = 1, 2, 3, und eine Strecke s, die krzer ist als der kleinste der drei Kreisdurchmesser.
Gesucht ist ein vierter Kreis k, der aus den drei Kreisen Sehnen der gegebenen Streckenlnge s herausschneidet.
2 Lsungsskizze
Zu jedem
der drei Kreise ki, i = 1, 2, 3, zeichnen wir einen konzentrischen
reduzierten Kreis ![]() mit dem
Radius:
mit dem
Radius:
![]() (1)
(1)
Dann
lsen wir das Apollonius-Problem fr die drei reduzierten Kreise ![]() .
.
Es gibt 23 = 8 Lsungen.
Mit ![]() als dem
Radius einer Lsung
als dem
Radius einer Lsung ![]() ist r mit
ist r mit
![]() (2)
(2)
der Radius einer Lsung fr unser Problem.
Die Aufgabe ist mit Zirkel und Lineal lsbar.
3 Exemplarische Lsung
Die Abbildung 1 zeigt die Aufgabenstellung, die Abbildungen 2 bis 5 eine Lsung.

Abb. 1: Aufgabenstellung
Als
erstes konstruieren wir die reduzierten Kreise ![]() , i = 1, 2,
3 (blau in Abb. 2).
, i = 1, 2,
3 (blau in Abb. 2).
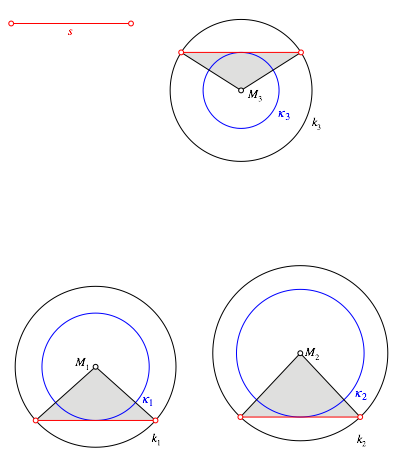
Abb. 2: Reduzierte Kreise
Nun kommt der aufwndigste Teil. Zu den drei reduzierten Kreisen suchen wir einen vierten Kreis, der alle drei berhrt. Dies ist das Problem des Apollonius von Perge (ca. 262 v. Chr. – ca. 190 v. Chr.). Es gibt 23 = 8 Lsungen je nach der Berhrung von innen oder von au§en. Das Problem ist mit Zirkel und Lineal lsbar, aber aufwndig. Einfacher geht es mit Hyperbeln nach Adriaan van Roomen (1561-1615).
Im Folgenden wird der Fall einer durchgehenden Berhrung von au§en weiterbearbeitet (Abb. 3).
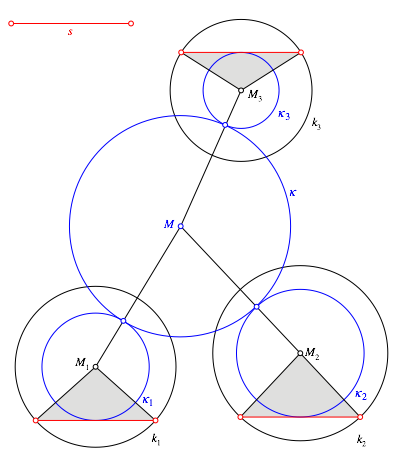
Abb. 3: Berhrender Kreis
Die Abbildung 4 zeigt nun, wie wir zu unserem gesuchten Kreis k kommen.
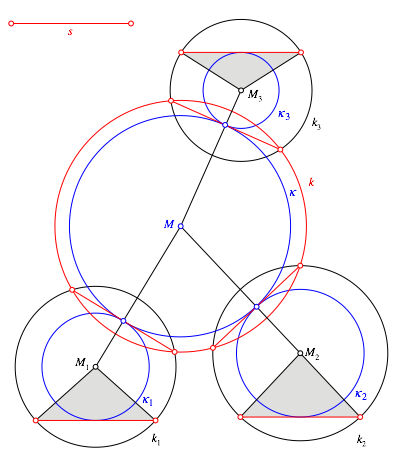
Abb. 4: Lsung unseres Problems
Die Abbildung 5 hat rein sthetischen Charakter.
Abb. 5: Voil