1 Problemstellung

Zu zwei Geraden in allgemeiner Lage zeichnen wir einen gleichseitigen blauen Zickzackweg (Abb. 1). Die blauen Strecken sind also alle gleich lang. Nun schneiden wir die Trägergeraden der blauen Strecken.

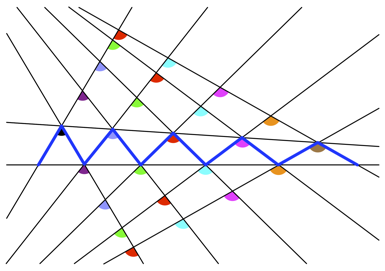
Abb. 1: Gleich große Winkel?

Die in der Abbildung 1 eingetragenen Winkel gleicher Farbe sind je gleich groß. Es sind also alle roten Winkel gleich, alle hellblauen und so weiter. Rote und hellblaue Winkel sind aber verschieden.

2 Bearbeitung

Wegen der strukturellen Translationssymmetrie (Wiederholung eines Konstruktionsmusters) können wir uns auf Winkel einer Farbe beschränken.

Wir greifen ein beliebiges der gleichschenkligen Dreiecke heraus und verwenden Bezeichnungen gemäß Abbildung 2.

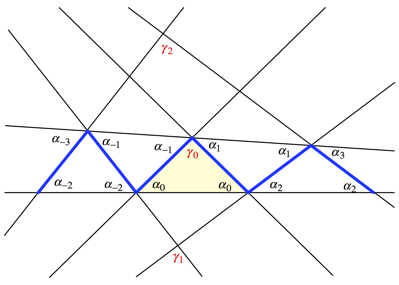
Abb. 2: Bezeichnungen

Zunächst ist:

(1)

Analog:

(2)

Addition der beiden Gleichungen in (2) liefert:

(3)

Wegen (1) ist:

(4)

Machen wir noch einen Schritt. Analog zu (2) ist:

(5)

Addition der beiden Zeilen in (5) ergibt:

(6)

Wegen (1) und (4) folgt:

(7)

Hier ein Wort zur Didaktik des Beweisens:

Auf der Sekundarstufe 1 (wofür dieses Problem gedacht ist) kann man nun „und so weiter“ sagen, und alle haben es verstanden. Auf der Sekundarstufe 2 spricht man von „vollständiger Induktion“ und plagt die Schülerinnen und Schüler mit einem elaborierten formalen Beweis, so dass die Köpfe rauchen und niemand was versteht. Auf Universitätsstufe spricht man von Induktion und alle nicken.

Jedenfalls ist:

(8)

Weiter ist nun:

(9)

Und:

(10)

Wegen (1) ist:

(11)

Im nächsten Schritt verwenden wir (4):

(12)

Allgemein gilt wegen (8):

(13)

Dies war zu zeigen.