1 Worum es geht

Versuch, einen elementargeometrischen Sachverhalt im rechtwinkligen Dreieck ohne Rechnen und Bezeichnungen zu beweisen.

2 Ausgangslage

Zu einem rechtwinkligen Dreieck zeichnen wir die beiden Kathetenquadrate (Abb. 1) sowie die beiden eingezeichneten Eckverbindungen.

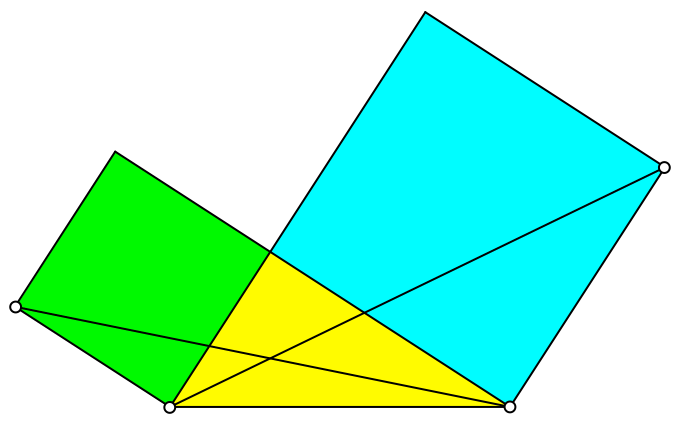
Abb. 1: Kathetenquadrate und Eckverbindungen

3 Problemstellung

Die beiden rot markierten Abschnitte sind gleich lang (Abb. 2). Dies ist zu zeigen.

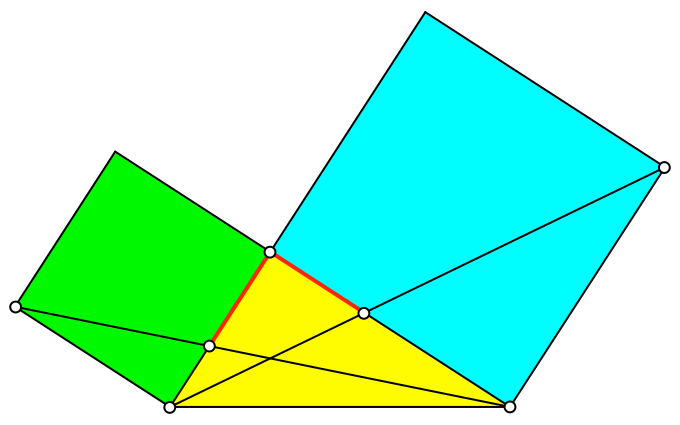
Abb. 2: Gleich lange Abschnitte

4 Beweis

4.1 Quadrat einpassen

Mit Hilfe der Winkelhalbierenden des rechten Winkels passen wir ein Quadrat ein mit der diametralen Ecke auf der Hypotenuse (rot in Abb. 3).

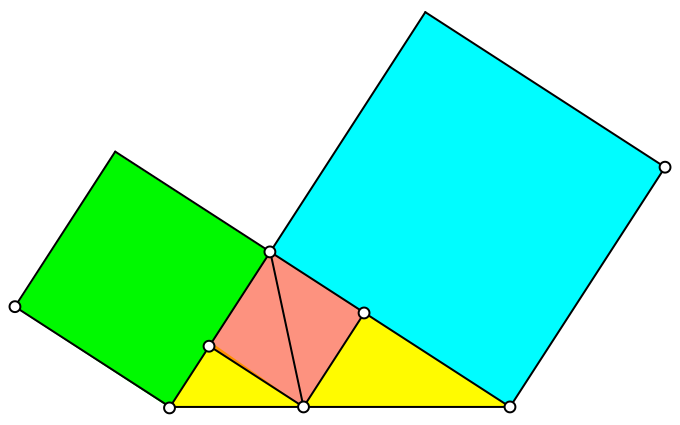
Abb. 3: Quadrat einpassen

4.2 Perspektivähnlichkeit

Das rote Quadrat und das grüne Kathetenquadrat sind perspektivähnlich mit dem Perspektivitätszentrum in der Ecke rechts unten (grün in Abb. 4).

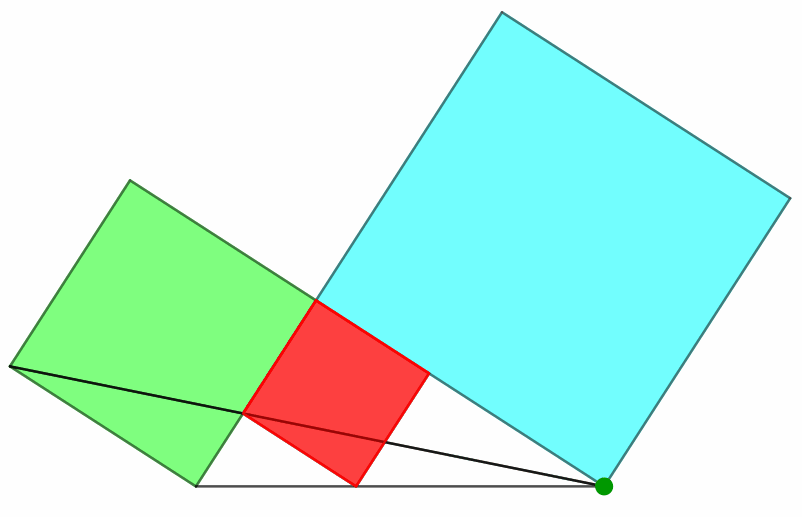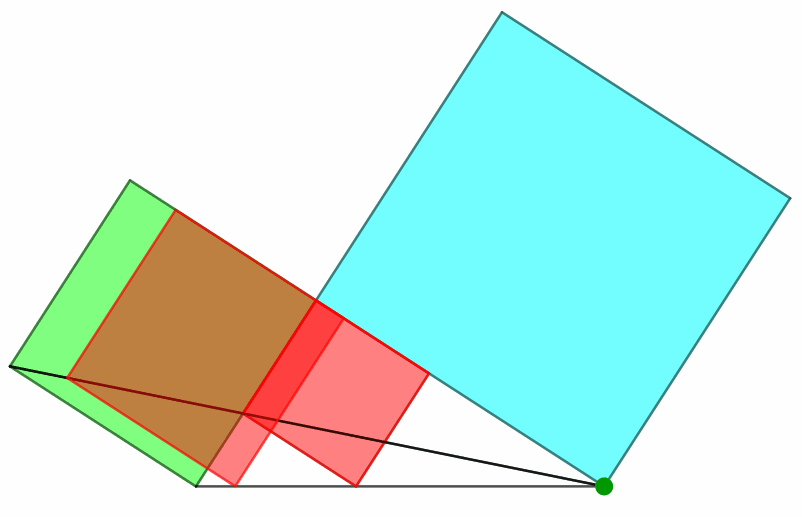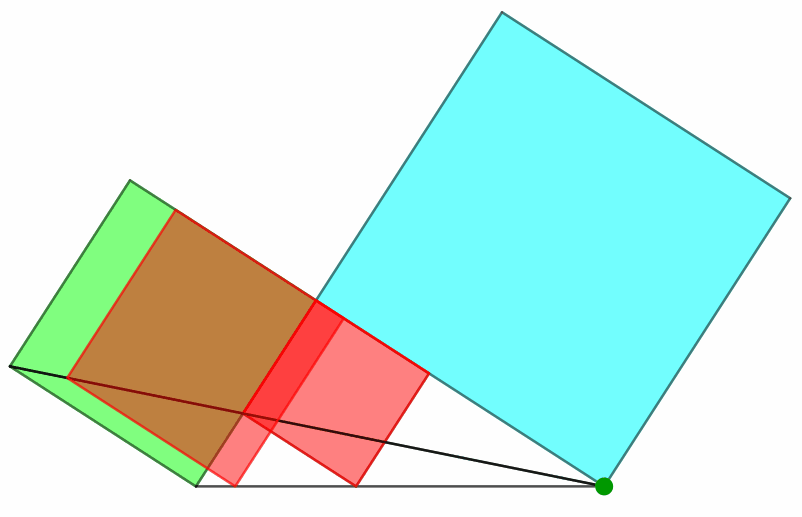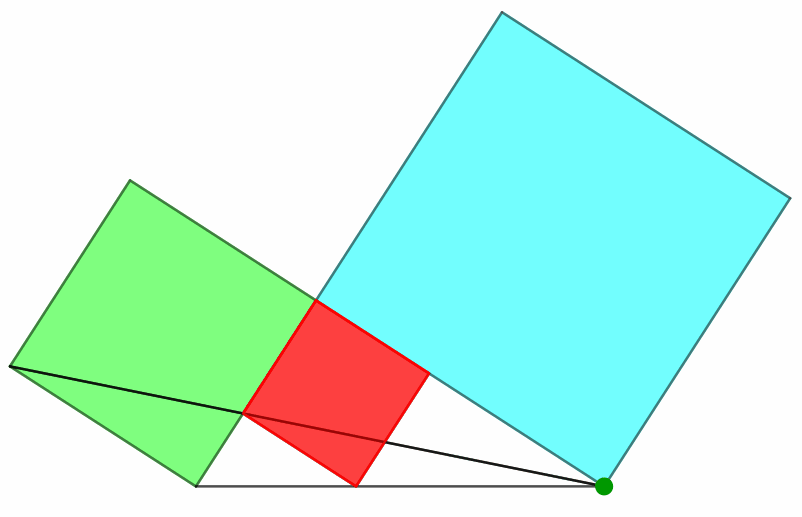
Abb. 4: Perspektivähnlichkeit

Entsprechendes gilt für das rote Quadrat und das blaue Kathetenquadrat (Abb. 5).

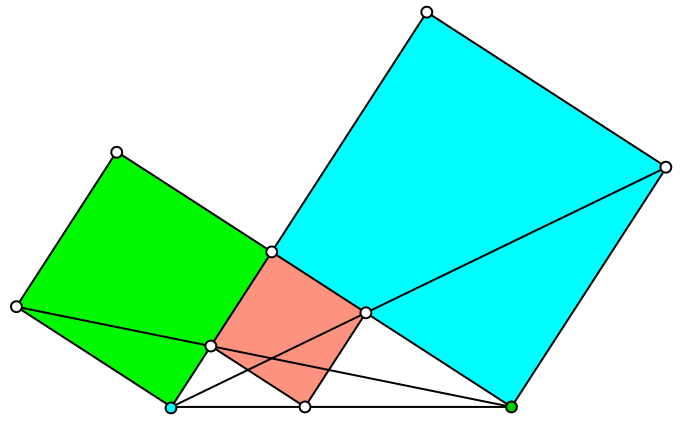
Abb. 5: Bahngeraden

Aus den Bahngeraden (Projektionsstrahlen) der Abbildung 5 lesen wir die Behauptung ab.

5 Verallgemeinerung

Einem beliebigen Dreieck setzen wir auf zwei Seiten Rhomben an, deren Winkel dem von den beiden Dreieckseiten eingeschlossenen Winkel entsprechen (Abb. 6). Die Seiten der Rhomben sind parallel zu den beiden Dreiecksseiten.

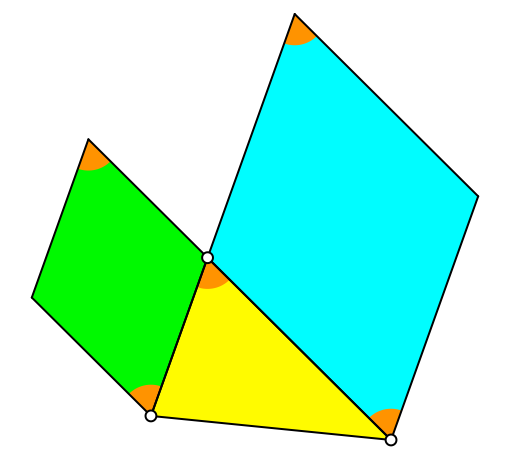
Abb. 6: Rhomben am Dreieck

Die Eckverbindungen führen zu zwei gleich lange Strecken (rot in Abb. 7).

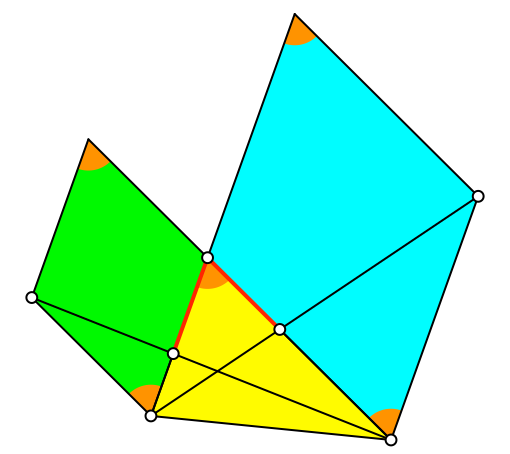
Abb. 7: Gleich lange Strecken

Beweis analog oder über eine affine Verzerrung der Figur der Abbildung 2.

6 Korollare

6.1 Zwei Quadrate und ein drittes

Wir fügen zwei Quadrate übereck aneinander und verbinden die Ecken gemäß Abbildung 8.

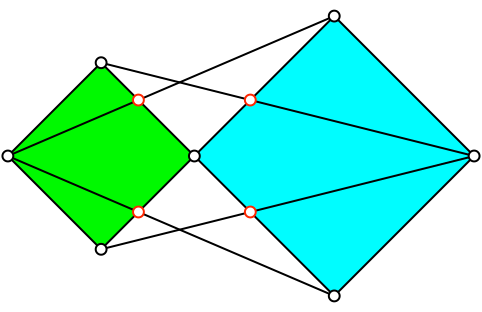
Abb. 8: Zwei Quadrate

Die roten Schnittpunkte sind Ecken eines dritten Quadrates (Abb. 9 und 10).

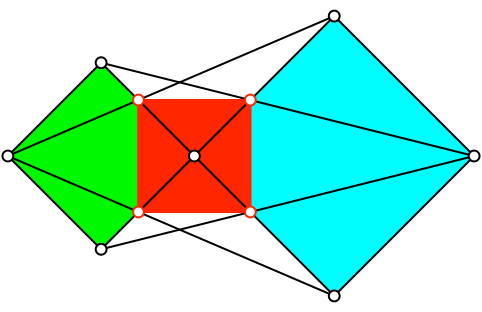
Abb. 3: Drittes Quadrat

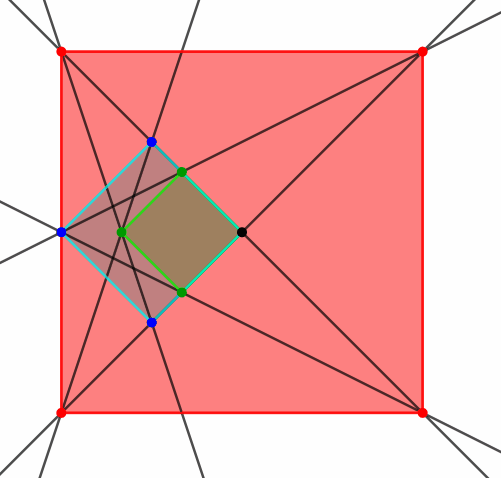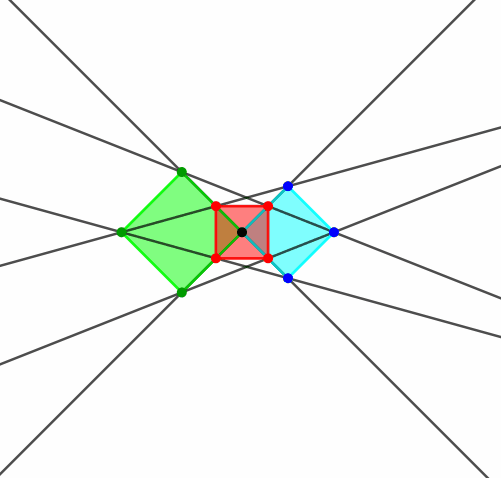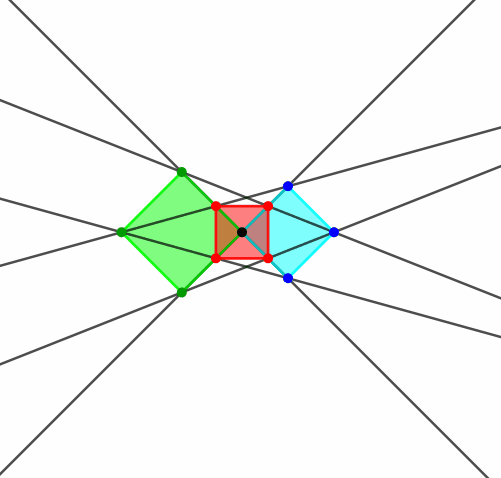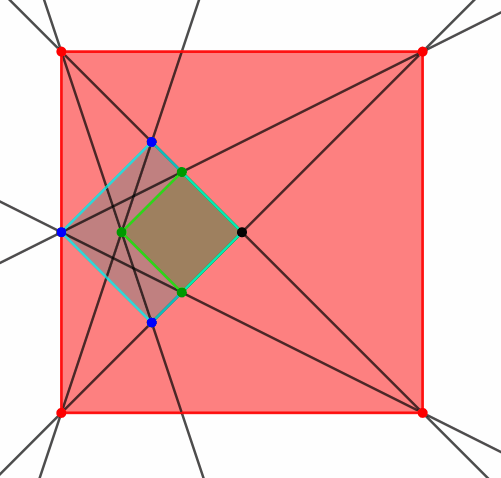
Abb. 10: Zwei Quadrate und ein drittes

6.2 Zwei Rhomben und ein Rechteck

Die entsprechende Konstruktion mit zwei ähnlichen Rhomben führt zu einem Rechteck (Abb. 11). Das Seitenverhältnis des Rechteckes ist gleich dem Diagonalenverhältnis der Rhomben.

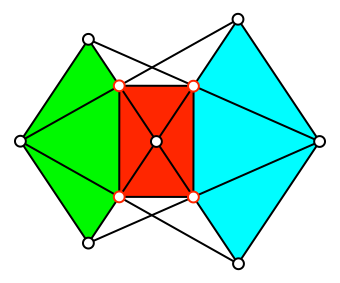
Abb. 11: Zwei Rhomben und ein Rechteck

Literatur

Posamentier, Alfred S. and Geretschläger, Robert: Geometric Gems: An Appreciation for Geometric Curiosities. Volume 1: The Wonders of Triangles. Worlds Scientific. 2024.