Hans Walser, [20230706]
Gleichseitige Dreiecke und Goldener Schnitt
Einem rechtwinklig-gleichseitigen Dreieck setzen wir auf den Katheten gleichseitige Dreiecke an (Abb. 1).
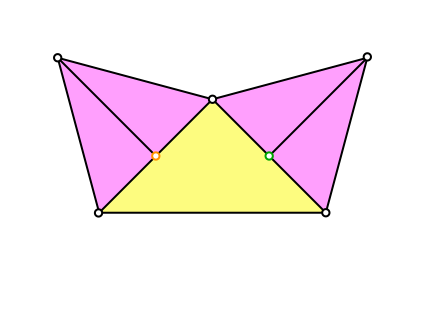
Abb. 1: Gleichseitige Dreiecke ansetzen
Wir zeichnen einen Kreis um den Mittelpunkt der einen Kathete des rechtwinklig-gleichschenkligen Dreiecks durch die Spitze des zugehörigen gleichseitigen Dreieckes (Abb. 2).
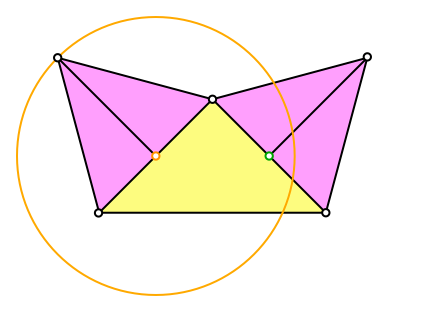
Abb. 2: Erster Kreis
Entsprechend verfahren wir mit dem zweiten gleichseitigen Dreieck (Abb. 3). Die beiden Kreise schneiden sich auf der Symmetrieachse der Figur.
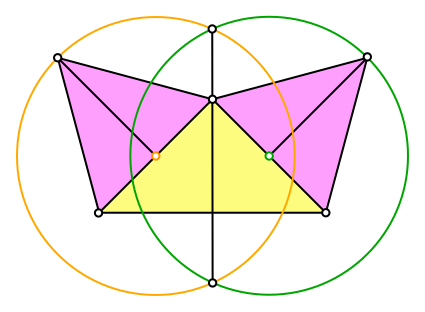
Abb. 3: Zweiter Kreis
Auf der Symmetrieachse ergibt sich eine Unterteilung im Verhältnis des Goldenen Schnittes, und zwar in der Reihenfolge Minor-Mayor-Minor (Abb. 4).
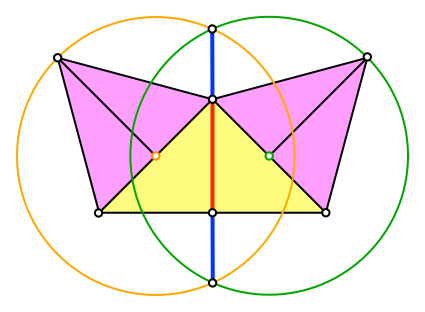
Abb.
4: Minor-Major-Minor
Nachweis durch Rechnen.
Weblinks
Hans Walser: DIN-Format und Goldener Schnitt
Hans Walser: Goldener Schnitt im rechtwinkligen Dreieck
http://www.walser-h-m.ch/hans/Miniaturen/G/Goldener_Schnitt_i_r_Dr/Goldener_Schnitt_i_r_Dr.html