Hans Walser, [20221204]

Gleichseitiges Fünfeck

1 Worum geht es?

Spezielle Konfigurationen eines symmetrischen gleichseitigen Fünfeckes

2 Gelenkmodell

Wir arbeiten mit einem Gelenkmodell eines gleichseitigen Fünfeckes (Abb. 1).

Abb. 1: Reales Gelenkmodell

3 Symmetrische Anordnung

Eine Seite und damit ihr beiden Endpunkte halten wir fest, den gegenüberliegenden Eckpunkt bewegen wir auf der Mittelsenkrechten dieser Seiten (Abb. 2). Dabei nehmen wir an, dass die beiden zum bewegten Eckpunkt benachbarten Eckpunkte durch die Schwerkraft nach unten gezogen werden. Daher haben wir oberhalb und unterhalb der festgehaltenen Seite unterschiedliche Figuren.

Abb. 2: Symmetrische Anordnung

4 Sonderfälle

Das Fünfeck habe die Seitenlänge 1. Die beiden festen Eckpunkte die Koordinaten (–0.5, 0) und (0.5, 0), der variable Punkt auf der Symmetrieachse die Koordinaten (0, h). Wir diskutieren die Figuren für ausgewählte Werte von h.

In fast allen Beispielen findet sich mit einigen Handgriffen der Goldene Schnitt. In den Abbildungen dazu wird jeweils die längere Teilstrecke („Major“) rot und die kürzere („Minor“) blau eingezeichnet.

4.1 Gleichschenkliges Dreieck

Mit h = sqrt(15)/2 ≈ 1.9365 erhalten wir ein gleichschenkliges Dreieck mit dem Seitenverhältnis 2:2:1 (Abb. 3). Den Goldenen Schnitt finden wir durch Einzeichnen zweier gleichseitiger Dreiecke.

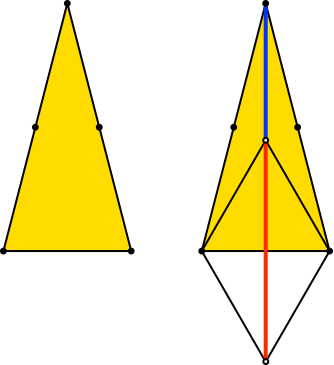
Abb. 3: Gleichschenkliges Dreieck

4.2 Gleichseitiges Dreieck

Mit h = 1 + sqrt(3)/2 ≈ 1.8660 ergibt sich ein gleichseitiges Dreieck (Abb. 4). Wir haben zusätzlich einen Ausleger, der als Strecke doppelt zu zählen ist. Den Goldenen Schnitt finden wir durch Hissen einer quadratischen Fahne.

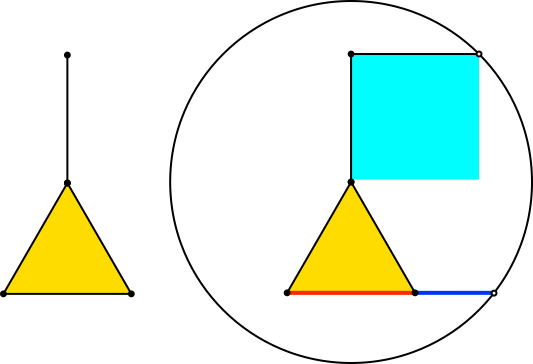
Abb. 4: Gleichseitiges Dreieck

4.3 Gleiche Flächeninhalte und eine Approximation

Für h = (sqrt(15 + 48*sqrt(10)) + sqrt(125 + 62*sqrt(10)))/(12 + 2*sqrt(10)) ≈ 1.6826 ergibt sich eine merkwürdige Figur (Abb. 5). Es ergibt sich ein Obelisk mit Sockel, wobei der Obelisk und der Sockel denselben Flächeninhalt haben.

Abb. 5: Obelisk mit Sockel

Durch Fixieren mit einer Schraube erhalten wir im realen Modell eine Approximation dieses Obelisken (Abb. 6).

Abb. 6: Approximation

Der Flächeninhalt des Viereckes ist etwa 3.82% größer als der Flächeninhalt des Sockeldreiecks.

Den Goldenen Schnitt habe ich nicht gefunden.

4.4 Goldener Obelisk

Mit h = sqrt(4*(1/2 + sqrt(5)/2)^2 - 1)/2 ≈ 1.5388 ergibt sich eine Figur, die sich in ein regelmäßiges Fünfeck gleicher Seitenlänge 1 einpassen lässt (Abb. 7). Damit ergibt sich auch der Goldene Schnitt.

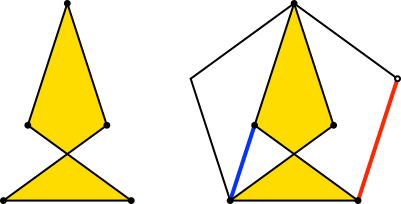
Abb. 7: Einpassen ins regelmäßige Fünfeck

4.5 Gleichseitiges Dreieck

Mit h = sqrt(3)/2 ≈ 0.866 ergibt sich wiederum ein gleichseitiges Dreieck (Abb. 8). Die Basisseite ist dreifach zu zählen. Den Goldenen Schnitt finden wir mit der Konstruktion von George Odom.

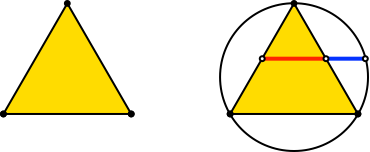
Abb. 8: Gleichseitiges Dreieck

4.6 Pentagramm

Mit h = sqrt(10 - 2*sqrt(5))/(2 + 2*sqrt(5)) ≈ 0.3633 ergibt sich ein regelmäßiges Pentagramm ( Abb. 9). Den Goldenen Schnitt finden wir an allen Ecken und Enden.

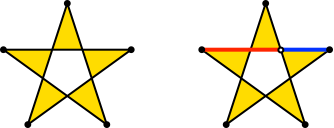
Abb. 9: Pentagramm

4.7 Gleichschenklige Dreiecke

Für h = 0 ergeben sich zwei gleichschenklige Dreiecke (Abb. 10). Diese sind ähnlich zum gleichschenkligen Dreieck der Abbildung 3, längenmäßig halb so groß.

Abb. 10: Gleichschenklige Dreiecke

4.8 Habregelmäßiges Fünfeck

Mit h = -sqrt(10 - 2*sqrt(5))/(2 + 2*sqrt(5)) ≈ -0.3633 ergibt sich das sogenannte halbregelmäßige Fünfeck ( Abb. 11). Es lässt sich in ein regelmäßiges Fünfeck einbetten. Den Goldenen Schnitt finden wir an allen Ecken und Enden.

Abb. 11: Halbregelmäßiges Fünfeck

4.9 Halbes Sechseck

Mit h = -sqrt(3)/2 ≈- 0.866 ergibt sich ein halbes regelmäßiges Sechseck (Abb. 12). Konstruktion des Goldenen Schnittes gemäß George Odom.

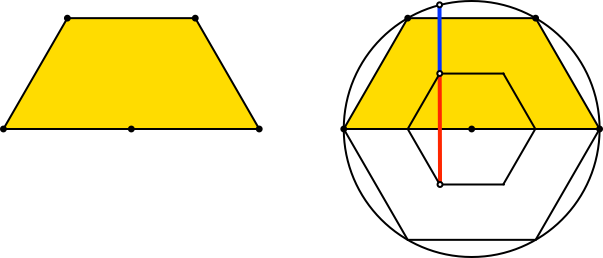
Abb. 12: Halbes Sechseck

4.10 Regelmäßiges Fünfeck

Mit h = -sqrt(4*(1/2 + sqrt(5)/2)^2 - 1)/2 ≈ -1.5388 erhalten wir das regelmäßige Fünfeck (Abb. 13). Prototyp für den Goldenen Schnitt.

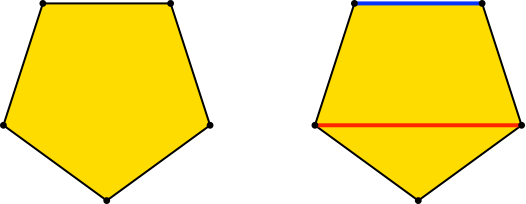
Abb. 13: Regelmäßiges Fünfeck

4.11 Quadrat und Dreieck

Mit h = -(1 + sqrt(3)/2) ≈ -1.8660 ergibt sich ein Fünfeck, das aus einem Quadrat und einem gleichseitigen Dreieck zusammengesetzt ist (Abb. 14).

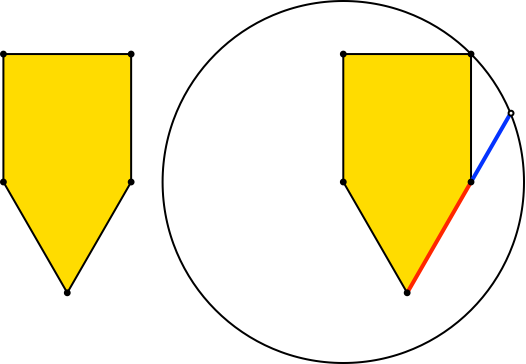
Abb. 14: Das Haus steht auf dem First

4.12 Gleichschenkliges Dreieck

Mit h = -sqrt(15)/2 ≈ -1.9365 erhalten wir wiederum ein gleichschenkliges Dreieck mit dem Seitenverhältnis 2:2:1 (Abb. 15). Den Goldenen Schnitt finden wir durch Einzeichnen zweier gleichseitiger Dreiecke.

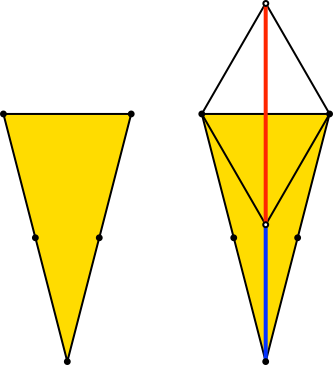
Abb. 15: Gleichschenkliges Dreieck