Hans Walser, [20220812]
Gleichseitiges Zwölfeck
1 Problemstellung
Zwölf gegebene Punkte sind so zu verbinden, dass ein Zwölfeck mit zwölf gleich langen Seiten entsteht.
Die Winkel brauchen nicht gleich zu sein. Die Seiten dürfen sich überschneiden.
Zu jedem Beispiel gibt es eine naheliegende sowie eine interessante Lösung.
2 Beispiele
2.1 Regelmäßiges Zwölfeck
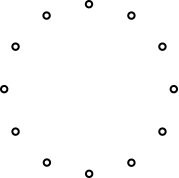
Abb. 1: Die zwölf Punkte
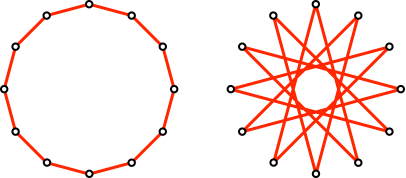
Abb. 2: Die beiden Lösungen
Die Streckenlängen der beiden Lösungen verhalten sich wie 1:(2+√(3)) ≈ 1: 3.732.
2.2 Kreuz
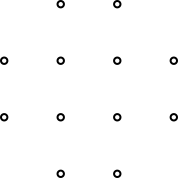
Abb. 3: Die zwölf Punkte
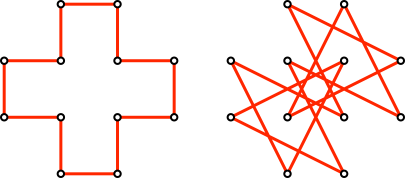
Abb. 4: Die beiden Lösungen
Die Streckenlängen der beiden Lösungen verhalten sich wie 1:√(5) ≈ 1: 2.236.
2.3 Stern
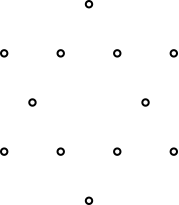
Abb. 5: Die zwölf Punkte
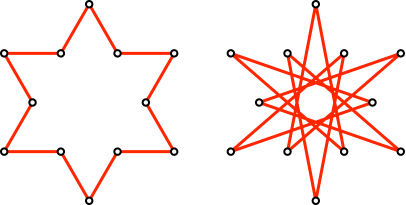
Abb. 6: Die beiden Lösungen
Die Streckenlängen der beiden Lösungen verhalten sich wie 1:√(7) ≈ 1: 2.646. Der Autor hat dies nicht erwartet.
2.4 Bienenhaus
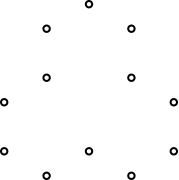
Abb. 7: Die zwölf Punkte
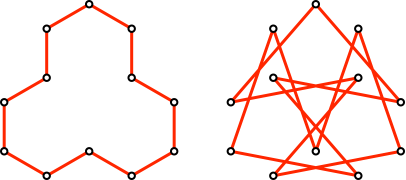
Abb. 8: Die beiden Lösungen
Die Streckenlängen der beiden Lösungen verhalten sich ebenfalls wie 1:√(7) ≈ 1: 2.646.