Hans Walser, [20220814]

Gleichseitiges Zwölfeck

1 Problemstellung

Zwölf gegebene Punkte im Raum oder auf der Kugel sind so zu verbinden, dass ein Zwölfeck mit zwölf gleich langen Seiten entsteht.

Die Winkel brauchen nicht gleich zu sein. Die Seiten dürfen sich überschneiden.

2 Sechskant-Prisma

Das einfachste Beispiel sind die zwölf Eckpunkte eines Sechskant-Prismas (Abb. 1). Die Höhe des Prismas ist gleich der Seitenlänge der Grundfläche. Die sechs Seitenflächen sind also Quadrate. Daher ergibt sich sehr einfach ein gleichseitiges Zwölfeck (Abb. 2).

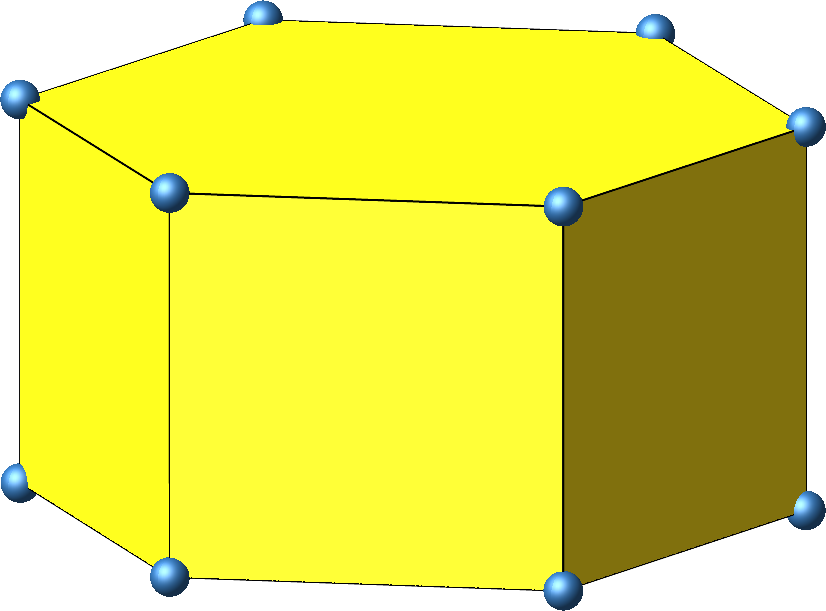
Abb. 1: Sechskant-Prisma

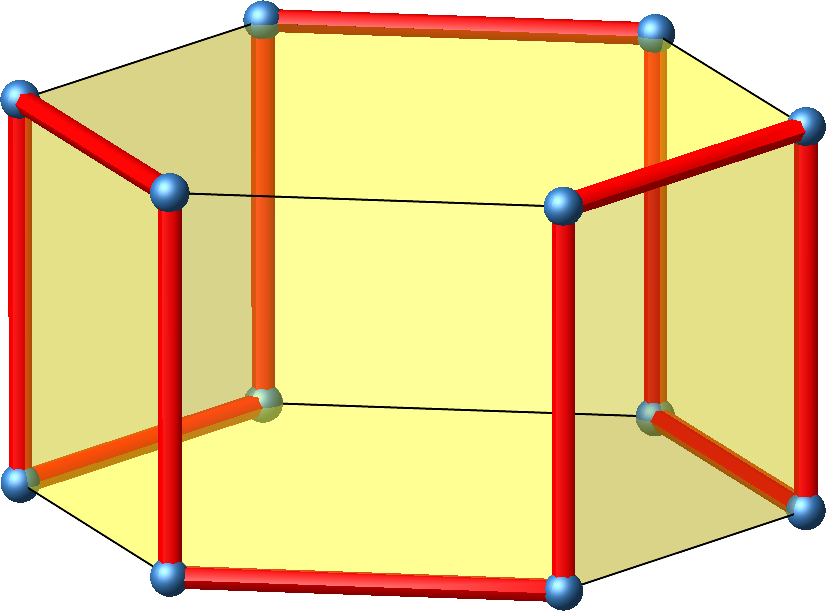
Abb. 2: Gleichseitiges Zwölfeck

Das Zwölfeck hat nicht nur gleich lange Seiten, sondern auch gleich große Winkel (rechte Winkel). Ein ebenes Vieleck mit gleich langen Seiten und gleich großen Winkeln wird als regelmäßiges Vieleck bezeichnet. Trotzdem ist es nicht sinnvoll, unser räumliches Zwölfeck als „regelmäßig“ zu bezeichnen.

Um dies einzusehen, betrachten wir zunächst die horizontale Strecke unten vorne sowie die vorangehende und die nachfolgende Strecke, welche beide senkrecht und parallel sind. Diese drei Strecken liegen in einer Ebene. Und nun nehmen wir die senkrecht stehende Strecke rechts und die vorangehende Strecke (also die horizontale Strecke unten vorne) und die nachfolgende Strecke, die sich in der oberen Etage befindet und nach hinten läuft. Diese drei Strecken liegen nicht in einer Ebene. Man kann das so formulieren, dass die senkrecht stehende Strecke zwischen Anfang und Ende um –120° tordiert (verdreht) worden ist (das Minuszeichen wegen der „rechte-Hand-Regel“). Wir haben also abwechslungsweise Strecken mit und Strecken ohne Torsion. Die Torsion, welche im Raum ein zusätzliches Kriterium zur Streckenlänge und den Winkeln ist, ist in unserem Beispiel nicht konstant. (Ein Streckenzug mit konstanter Länge, konstantem Winkel und konstanter nicht verschwindender Torsion ist eine Schraubenlinie. Bei der konstanten Torsion null erhalten wir einen ebenen regelmäßigen Streckenzug.)

Hingegen ist das gleichseitige Zwölfeck der Abbildung 2 punktsymmetrisch. Das Symmetriezentrum ist der Mittelpunkt des Sechskant-Prismas.

Wir können die Situation auf die Umkugel des Sechskant-Prismas projizieren (Abb. 3). Die Bogenlänge der einzelnen Bögen ist 2•arctan(½) ≈ 53.1301°.

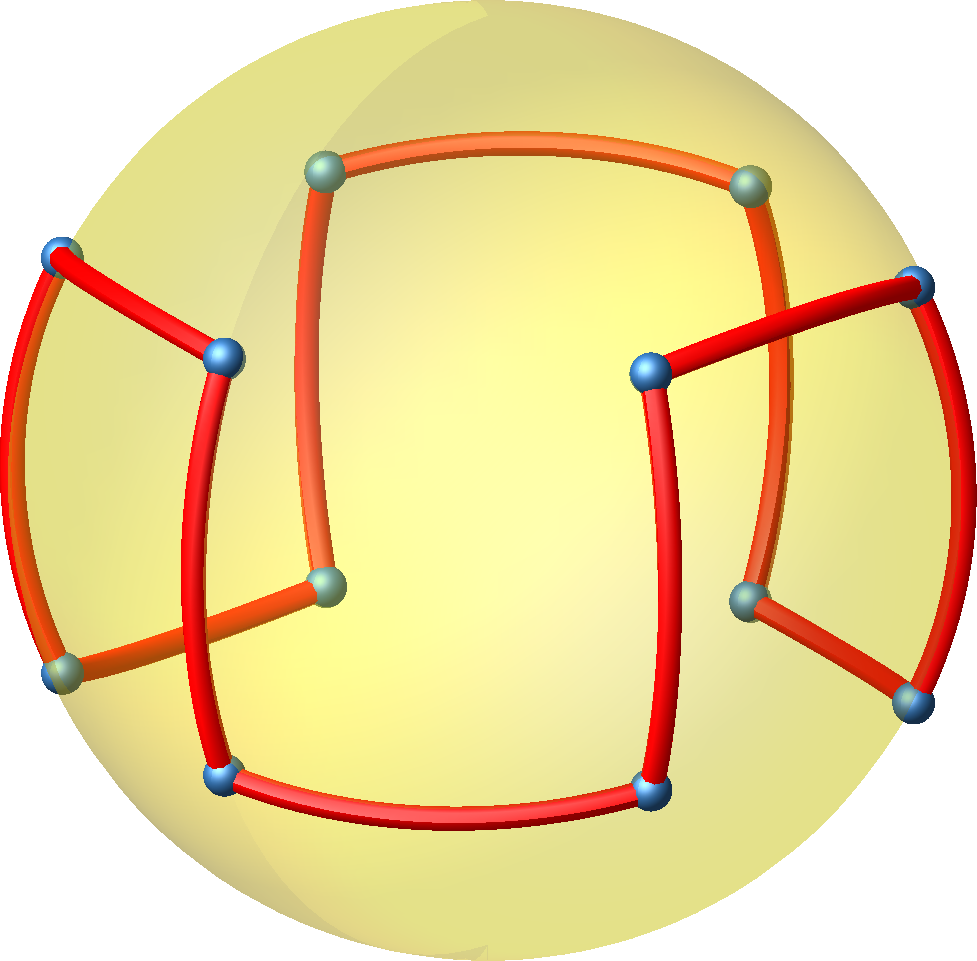
Abb. 3: Projektion auf Umkugel

Es gibt nun aber noch ein zweites gleichseitiges Zwölfeck mit den vorgegebenen zwölf Punkten (Abb. 4 und 5). Man kann mit dem Finger den Strecken nachfahren und auf zwölf zählen.

Die horizontalen Strecken halbieren sich gegenseitig, die schrägen dritteln sich.

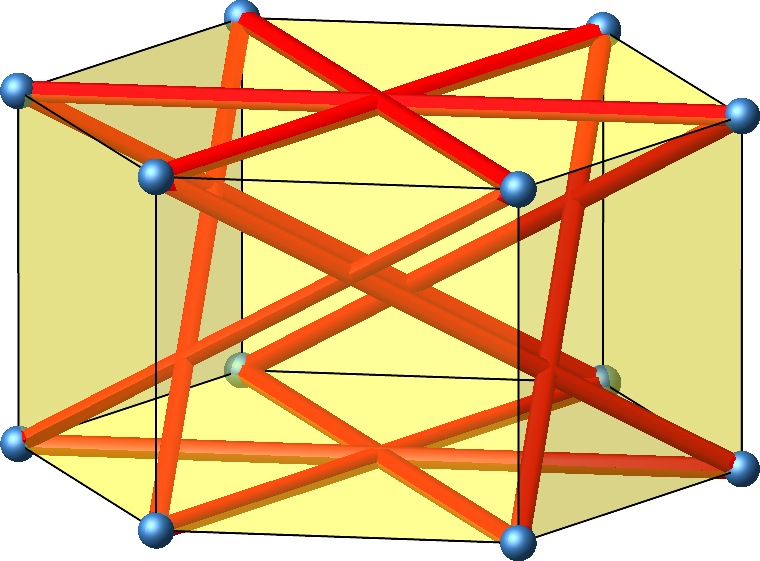
Abb. 4: Zweite Lösung

Abb. 5: Rotierende zweite Lösung

Auch diese Lösung kann auf die Umkugel projiziert werden (Abb. 6 und 7).

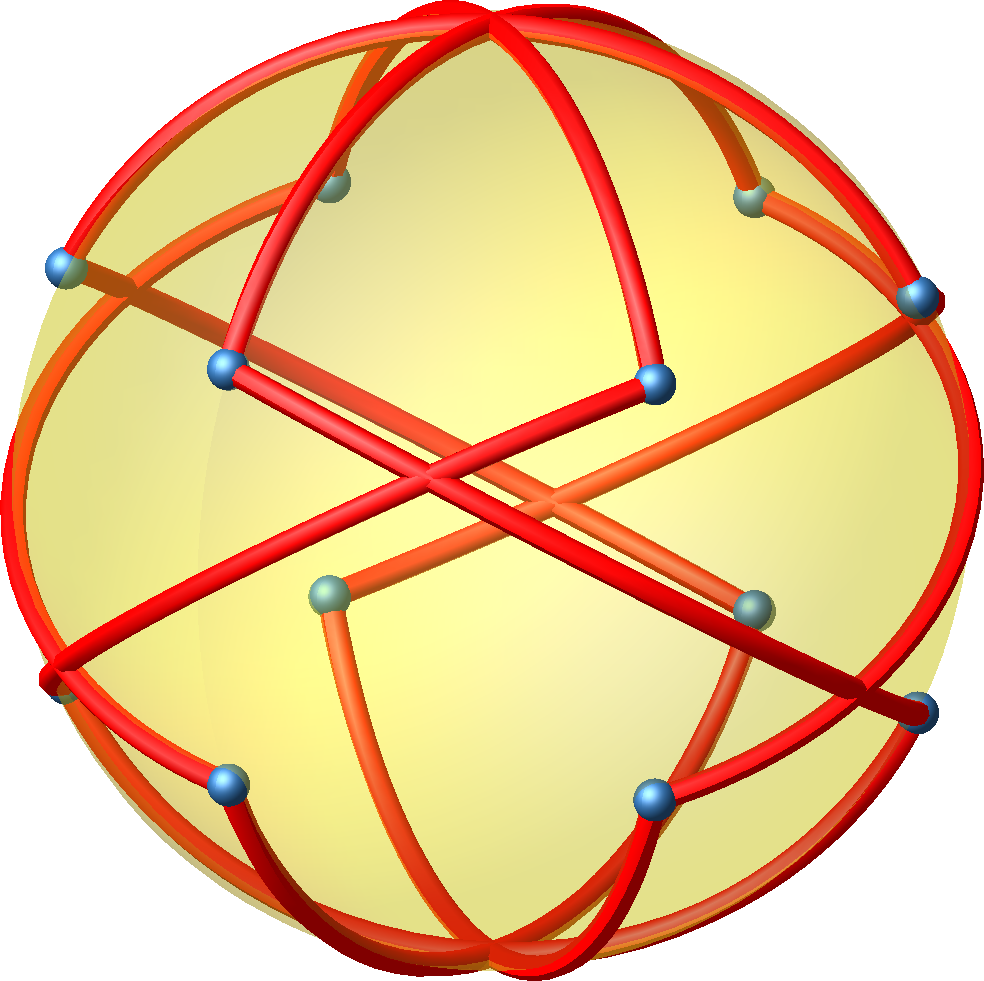
Abb. 6: Projektion auf Umkugel

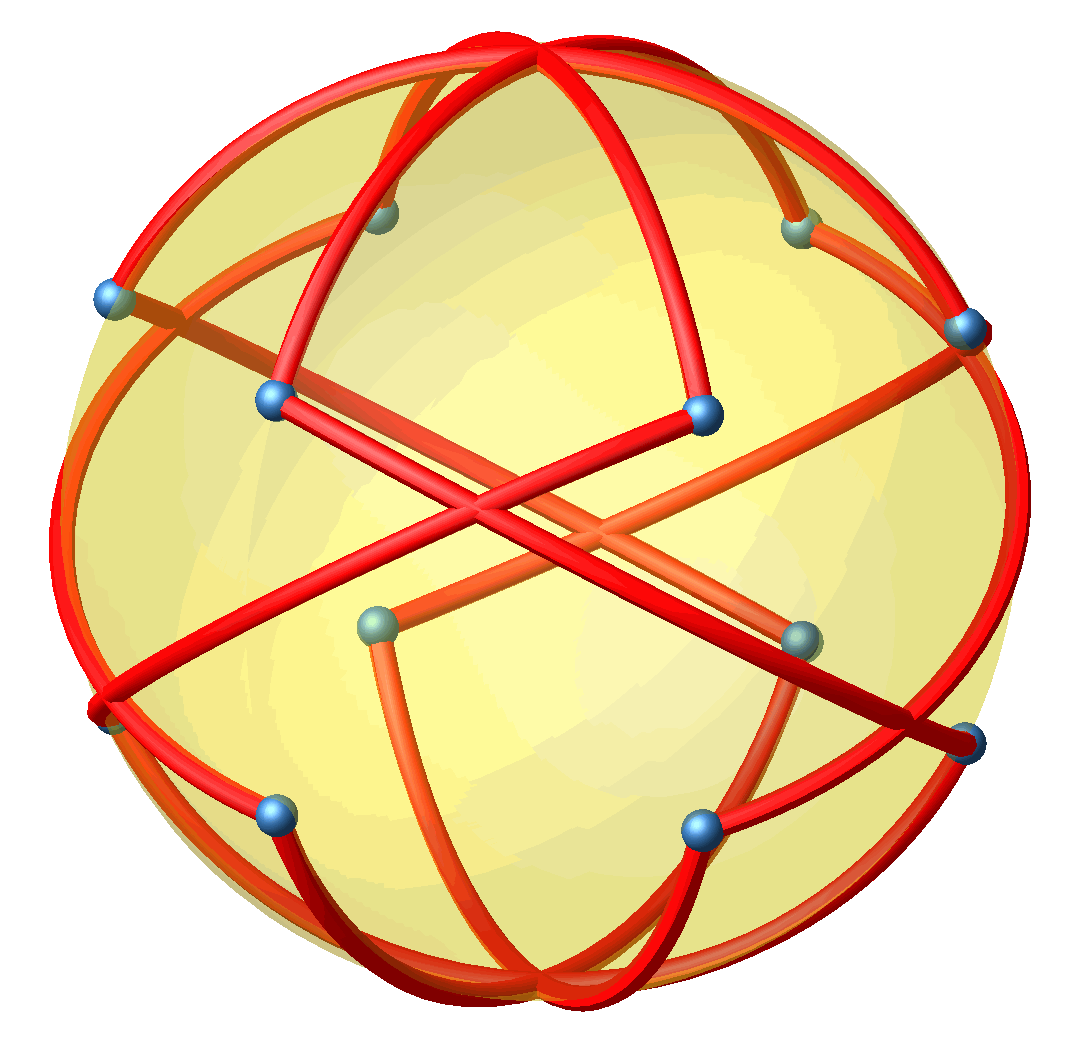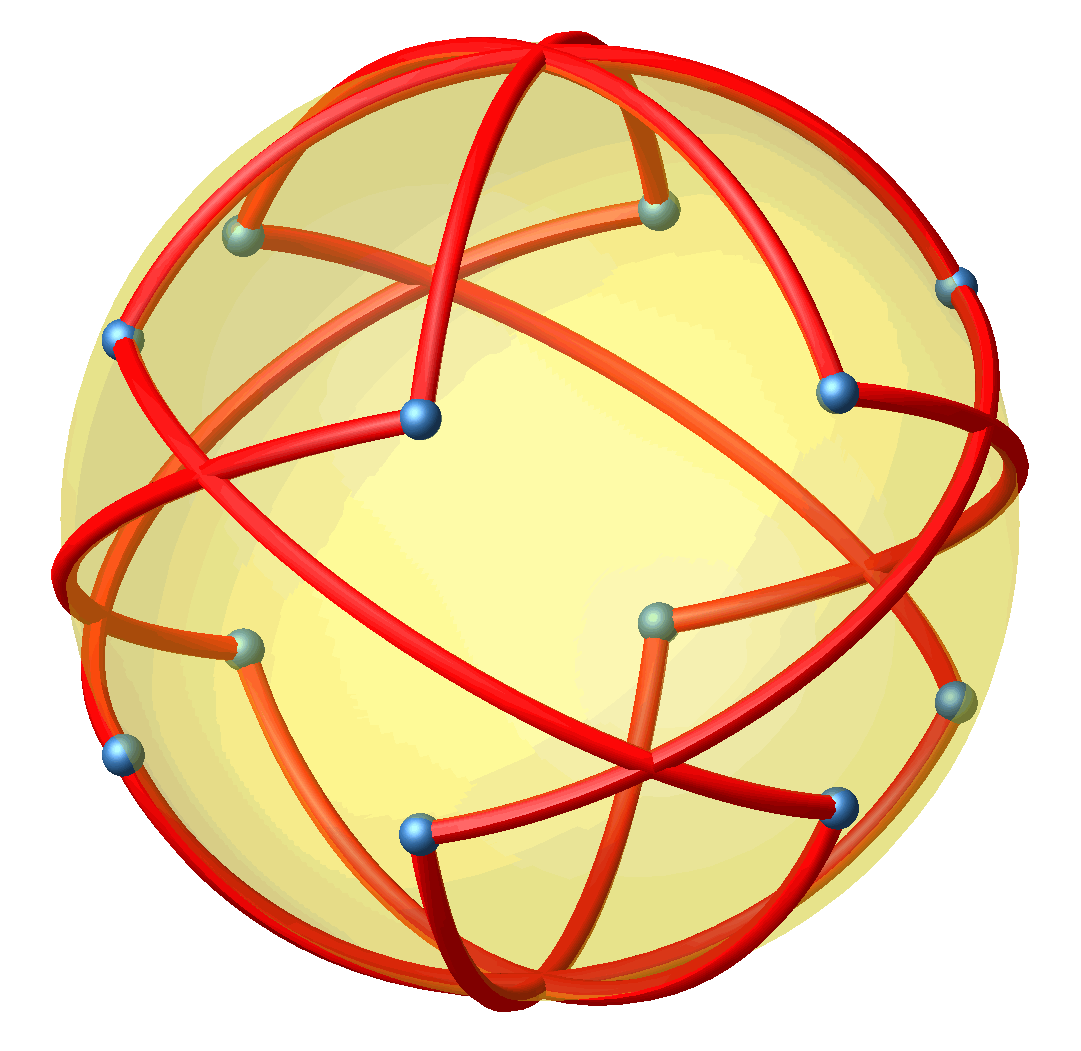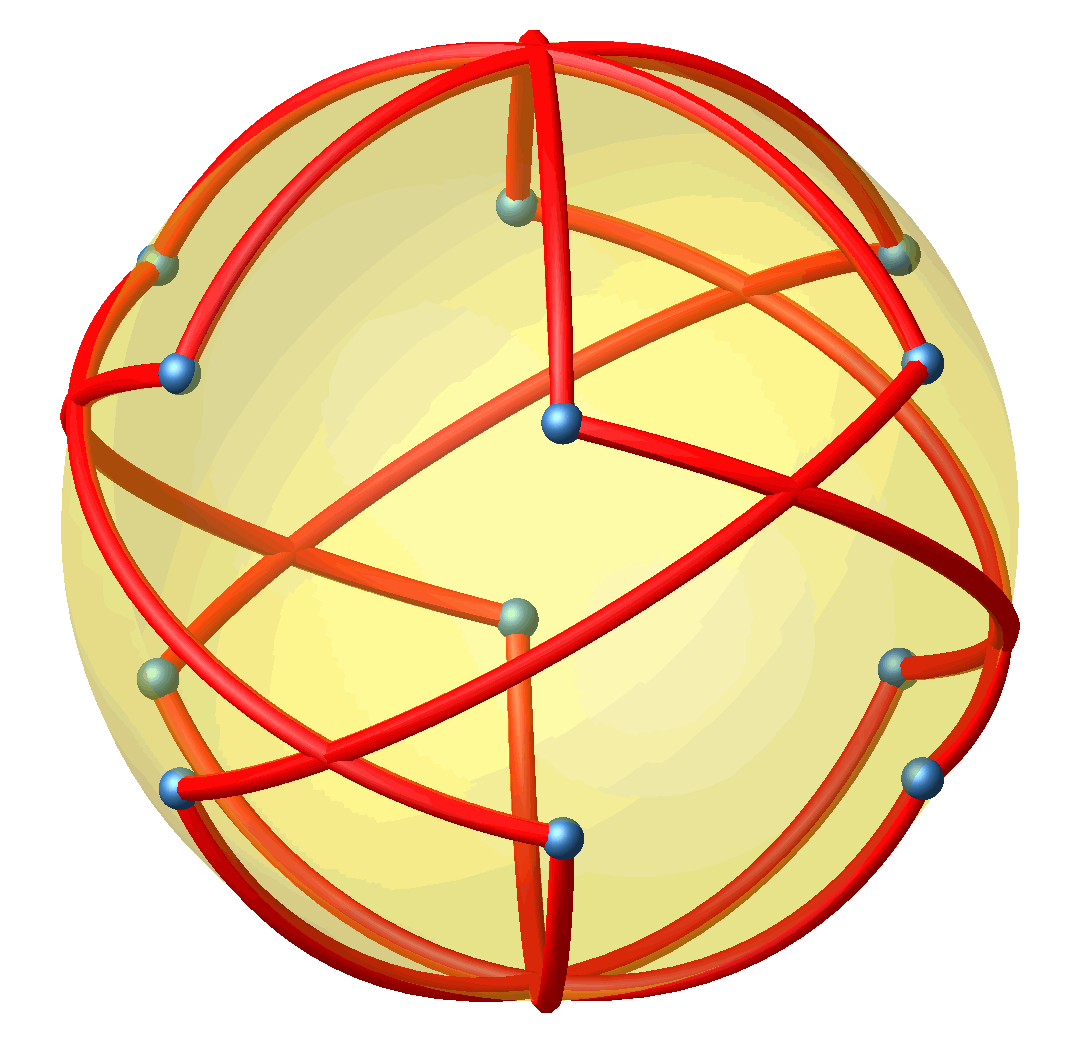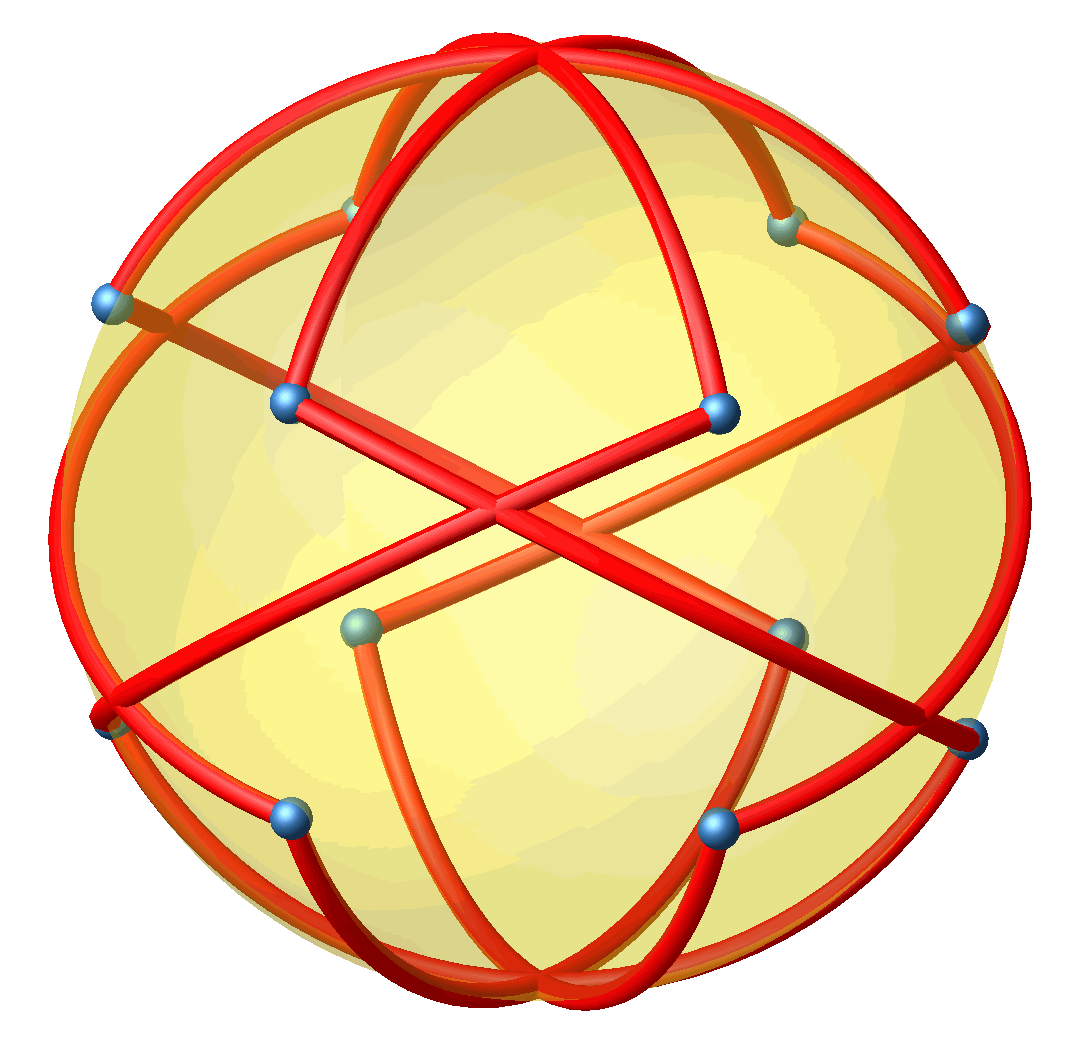
Abb. 7: Rotierende Projektion auf Kugel

Die zweite Lösung wird aus der ersten konstruiert wie folgt. Wir unterteilen das Zwölfeck der Abbildung 2 in Paare von je zwei aufeinanderfolgenden Strecken. Die Abbildung 8a zeigt ein Beispiel. Die beiden Strecken bilden einen rechten Winkel.

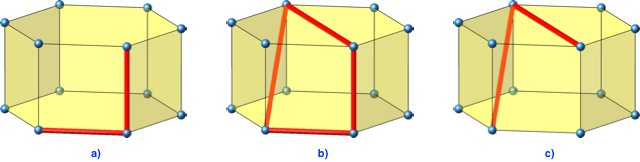
Abb. 8: Versetzen des Scheitelpunktes

Nun versetzen wir den Scheitelpunkt des rechten Winkels in seinen diametralen Punkt (Abb. 8b). Der neu entstandene Winkel hat zwei gleich lange Schenkel, die Schenkel sind genau doppelt so lang (nachrechnen!) wie die Schenkel des rechten Winkels. Der neue Winkel misst β = arccos(¾) ≈ 41.4096°. Nun entfernen wir den ursprünglichen rechten Winkel(Abb. 8c). Wenn wir nun mit jedem Paar aufeinanderfolgender Strecken so verfahren, ergibt sich aus dem Zwölfeck der Abbildung 2 jenes der Abbildung 4.

3 Antiprisma

Beim Antiprisma (Abb. 9) spielt die Höhe keine Rolle. Der äußere Zickzack ist bereits ein gleichseitiges Zwölfeck (Abb. 10).

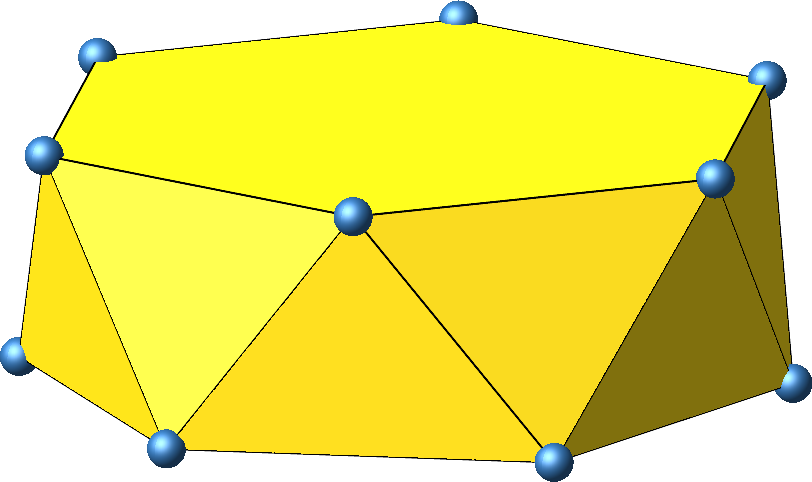
Abb. 9: Antiprisma

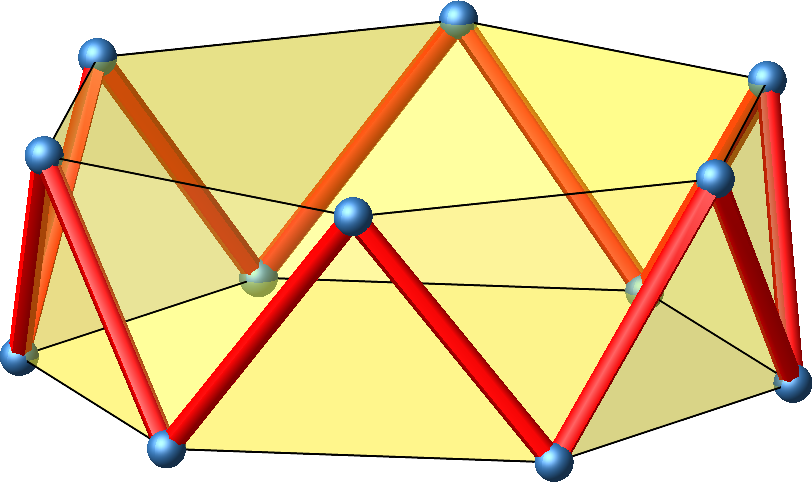
Abb. 10: Gleichseitiges Zwölfeck

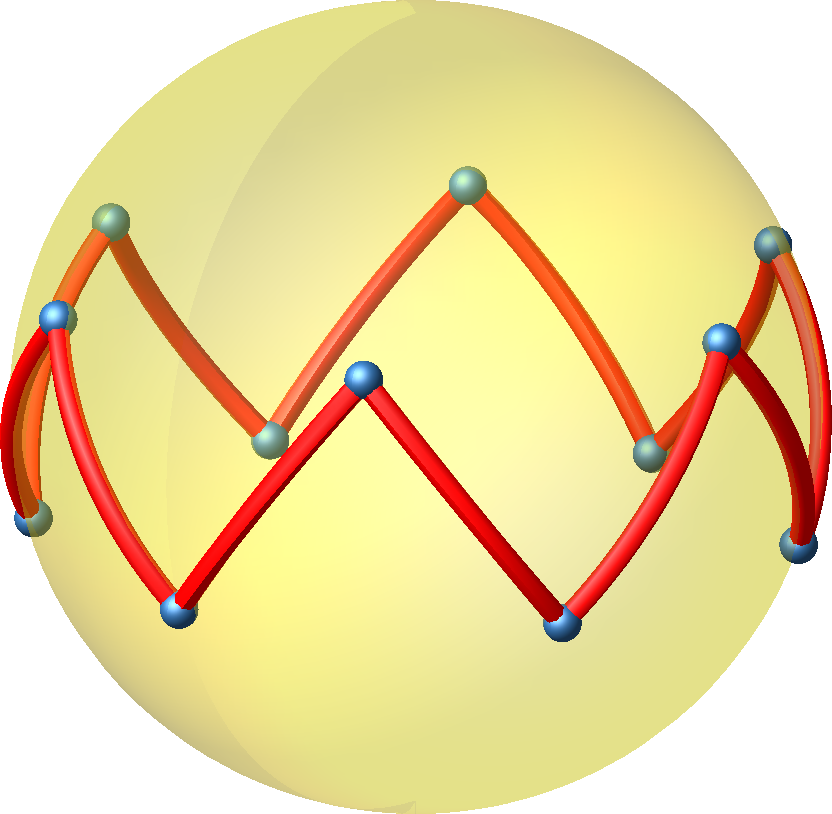
Abb. 11: Auf der Umkugel

Das Antiprisma ist nicht punktsymmetrisch. Wir finden aber eine zweite Lösung (Abb. 12), indem wir die Scheitelpunkte zum Beispiel in der oberen Etage mit dem jeweils in der oberen Etage gegenüberliegenden Punkt vertauschen.

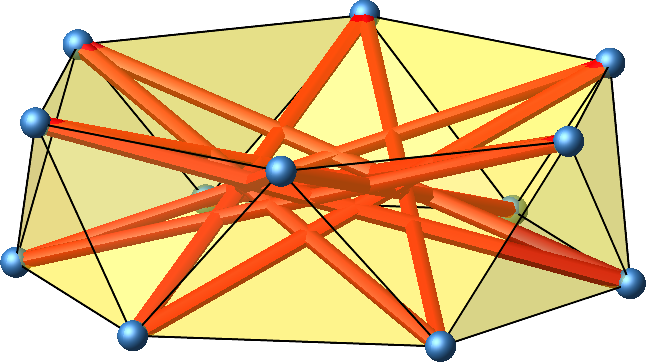
Abb. 12: Zweite Lösung

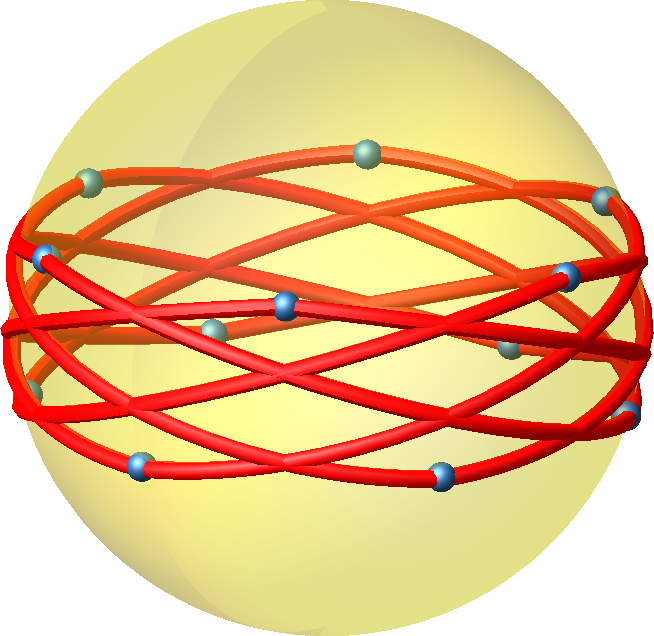
Abb. 13: Vogelnest

4 Ikosaeder

Das klassische Beispiel von zwölf regelmäßig im Raum angeordneten Punkten sind die Eckpunkte des Ikosaeders (Abb. 14). Es ist punktsymmetrisch.

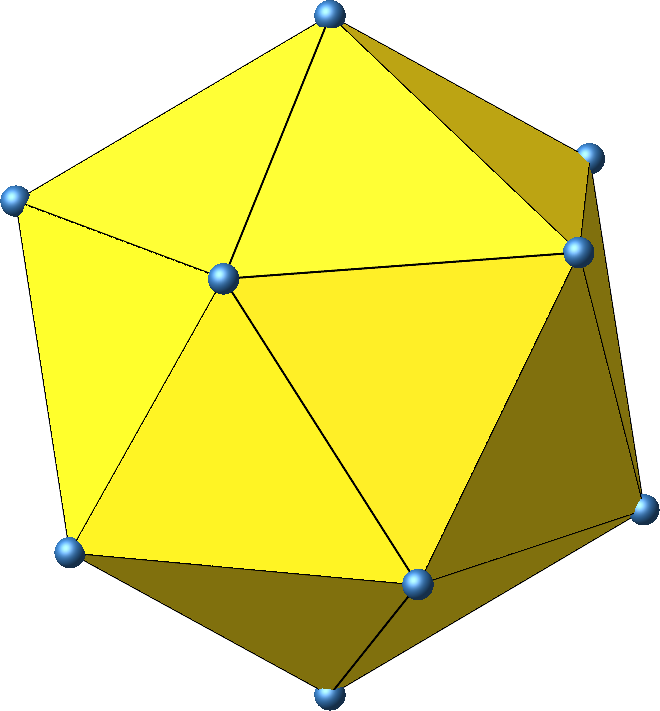
Abb. 14: Ikosaeder

Es gibt etliche Zwölfecke auf dem Ikosaeder, sogenannte Hamilton-Kreise, geschlossene Kantenzüge, die jeden Eckpunkt genau einmal durchfahren. Die Abbildung 15 zeigt ein Beispiel.

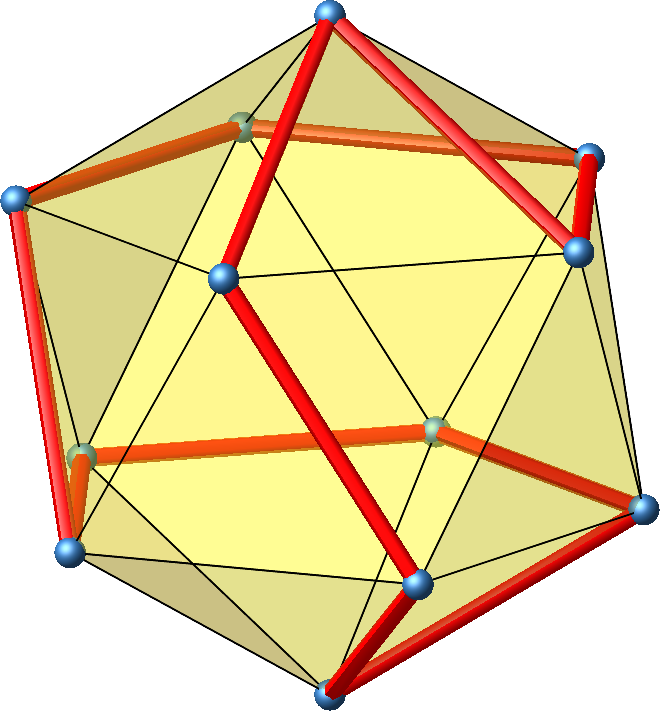
Abb. 15: Ein Zwölfeck auf dem Ikosaeder

Bei diesem Beispiel ist es allerdings nun leider so, dass die bisher angewandte Methode des Verschiebens jedes zweiten Scheitels in den diametralen Punkt nicht funktioniert. Man kann das so einsehen. Vom obersten Punkt („Nordpol“) zum untersten Punkt („Südpol“) sind es drei Strecken. Wenn nun der oberste Punkt festbleiben soll, muss der anschließende Punkt in den diametralen Punkt verschoben werden, der nächstanschließende Punkt aber festbleiben und der wiederum anschließende Punkt in den diametralen Punkt verschoben werden. Es muss also der unterste Punkt in den obersten Punkt verschoben werden und daher umgekehrt der oberste Punkt in den untersten. Dies steht im Widerspruch zur Annahme, dass der oberste Punkt festbleiben soll. Ein analoger Widerspruch entsteht, wenn wir den obersten Punkt in den untersten Punkt verschieben wollen.

Wir haben ein sogenanntes Paritätsproblem, ein Problem also mit „gerade“ und „ungerade“. Die Verschiebe-Methode ist nur anwendbar, wenn nirgends zwei diametrale Punkte durch eine ungerade Anzahl Strecken verbunden sind.

In der Abbildung 16 sind nun vier Strecken vom obersten zum untersten Punkt. Hingegen sind es vom Punkt ganz rechts in der unteren Etage zum diametralen Punkt ganz links in der oberen Etage nur drei Strecken (hintenherum) beziehungsweise neun Strecken vorneherum. Geht also auch nicht.

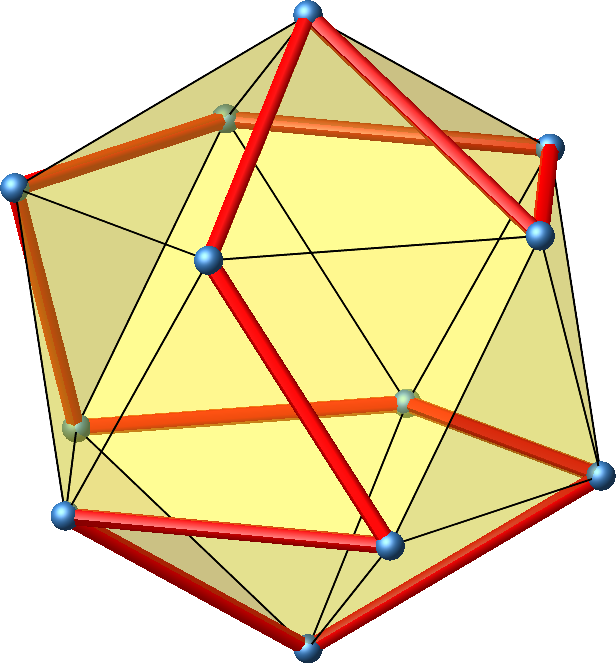
Abb. 16: Noch ein Zwölfeck auf dem Ikosaeder

Die Abbildung 17 zeigt in punktsymmetrisches Zwölfeck auf dem Ikosaeder. Von jedem Punkt aus sind es sechs Strecken bis zu seinem diametralen Punkt.

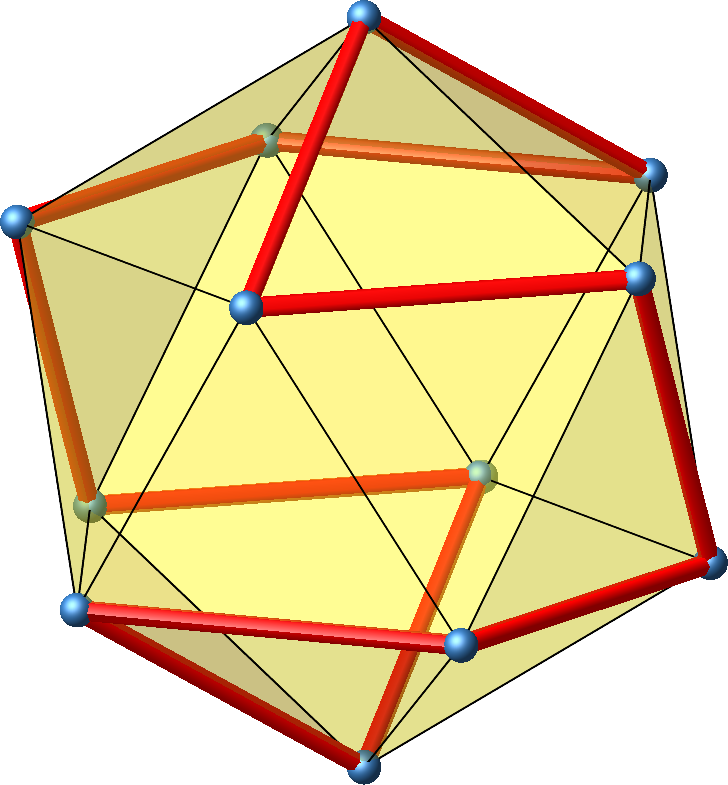
Abb. 17: Punktsymmetrisches gleichseitiges Zwölfeck

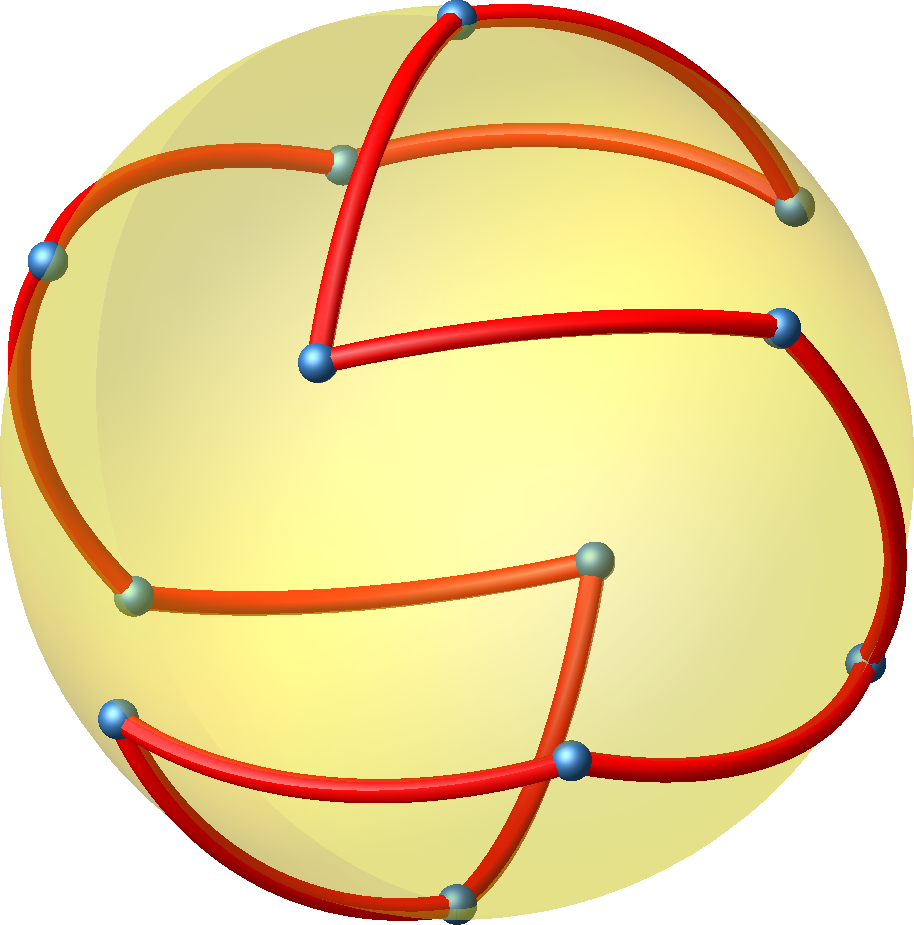
Abb. 18: Punktsymmetrische Lösung auf Umkugel

Damit können wir die Verschiebe-Methode anwenden (Abb. 19).

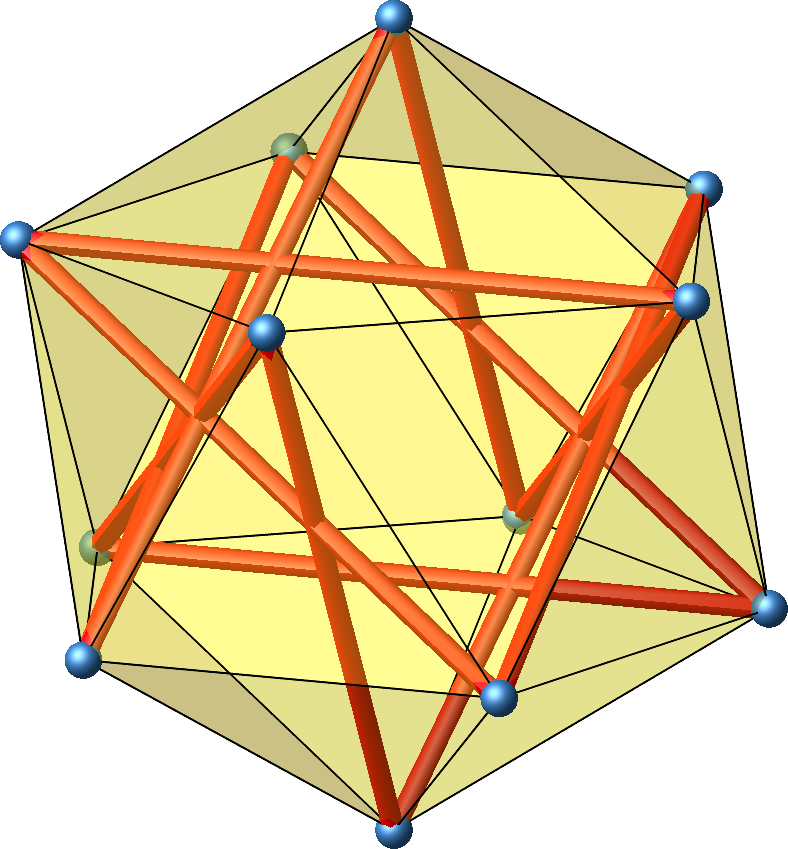
Abb. 19: Gleichseitiges Zwölfeck mit langen Seiten

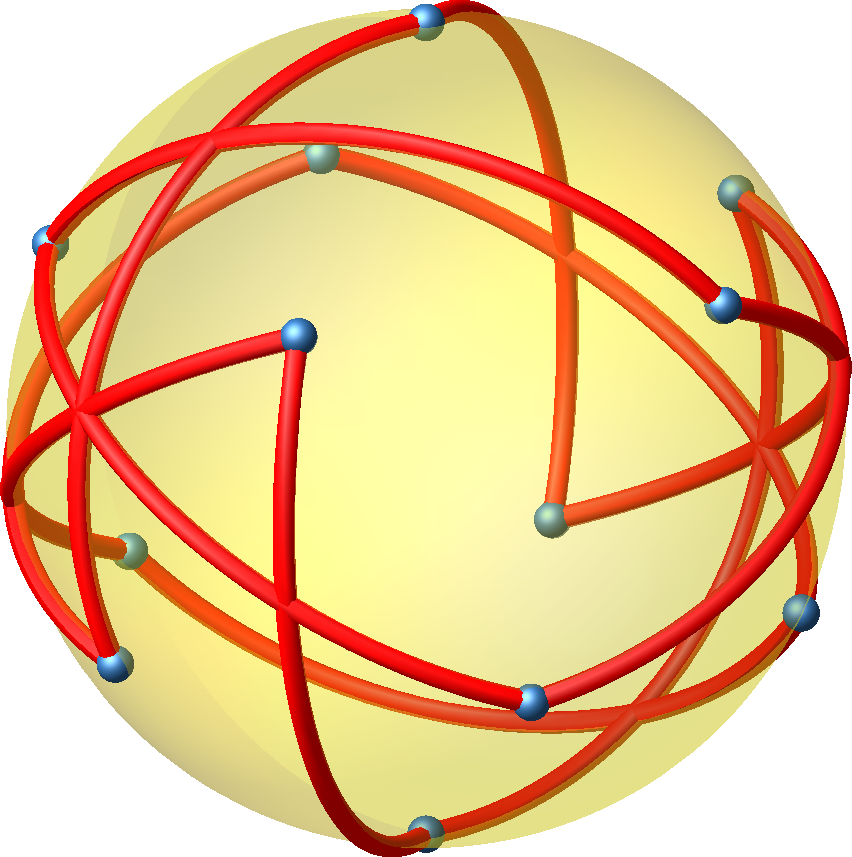
Abb. 20: Auf der Umkugel

Die Streckenlängen der beiden Zwölfecke der Abbildungen 17 beziehungsweise 19 verhalten sich wie 1: Φ. Dabei ist Φ der Goldene Schnitt:

In der Abbildung 19 schneiden die Strecken einander. Die Schnittpunkte unterteilen die Strecken im Verhältnis des Goldenen Schnittes.

5 Kuboktaeder

Das Kuboktaeder (Abb. 21) hat ebenfalls zwölf Eckpunkte.

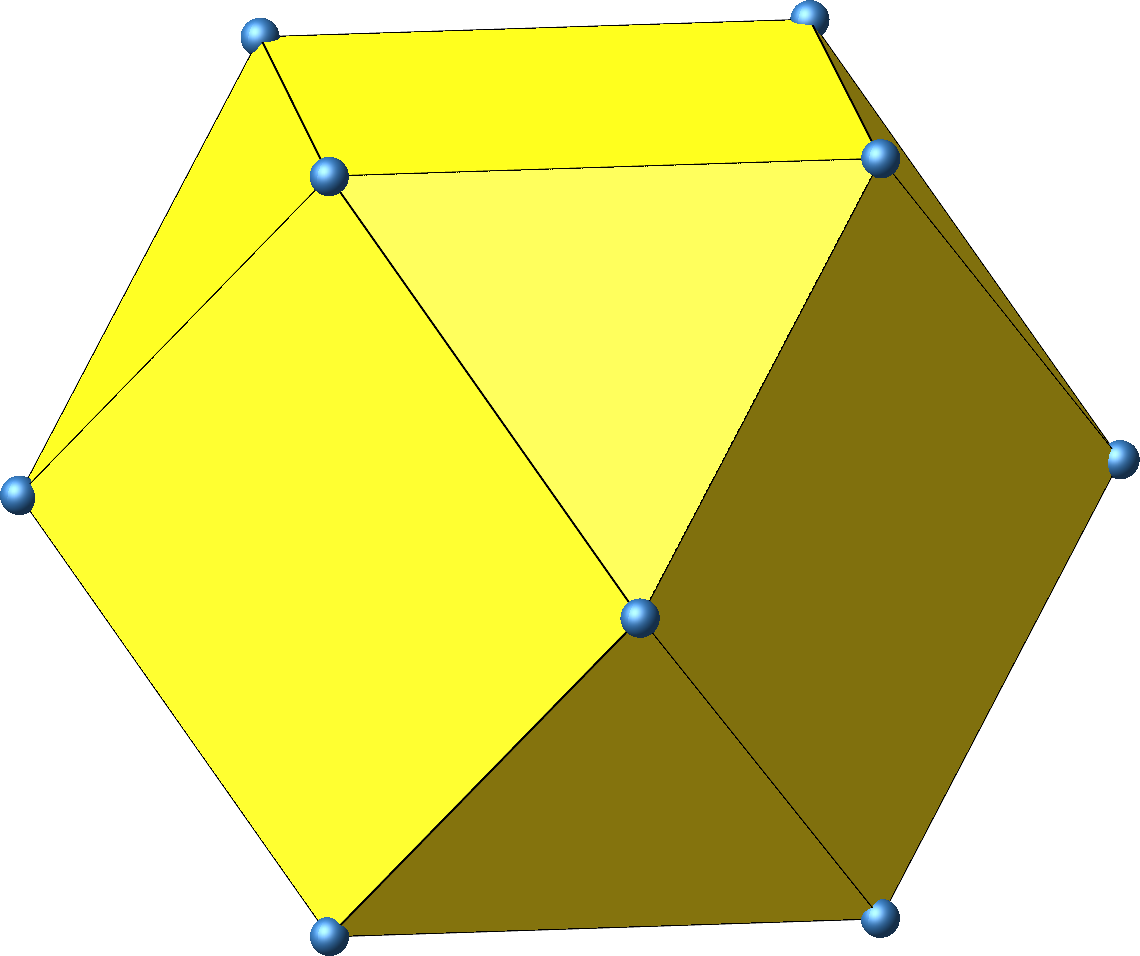
Abb. 21: Kuboktaeder

Die Abbildung 22 zeigt ein punktsymmetrisches gleichseitiges Zwölfeck auf dem Kuboktaeder.

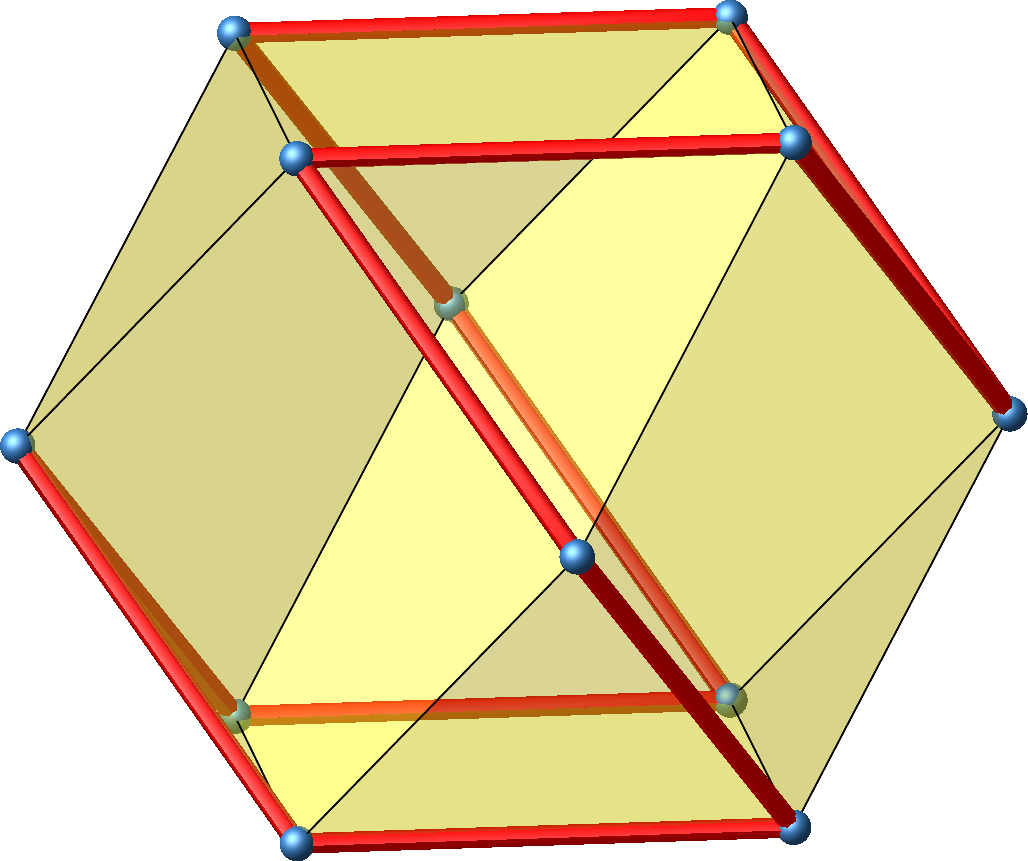
Abb. 22: Punktsymmetrisches gleichseitiges Zwölfeck

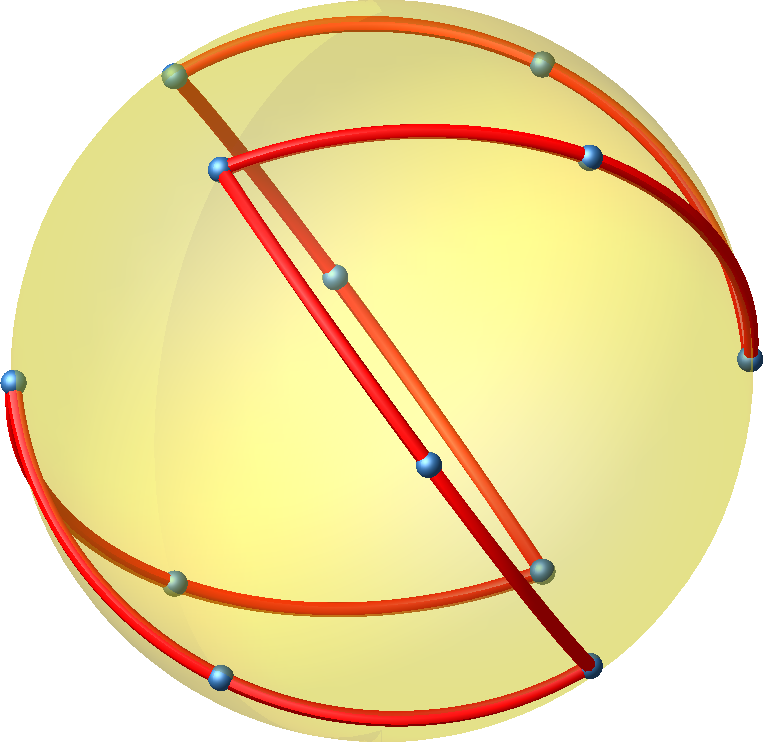
Abb. 23: Auf Umkugel

Die Verschiebe-Methode führt zu einem gleichseitigen Zwölfeck mit längeren Strecken (Abb. 24).

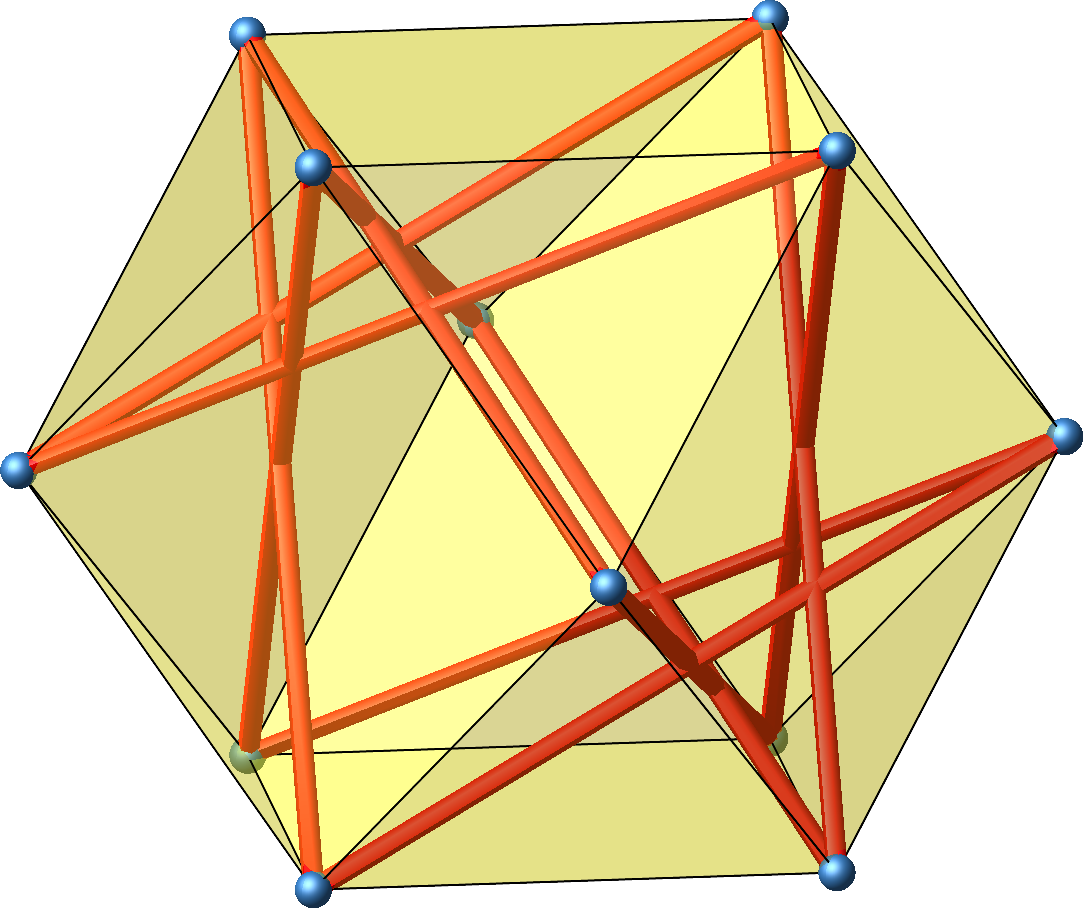
Abb. 24: Gleichseitiges Zwölfeck mit langen Seiten

Die Streckenlängen der beiden Zwölfecke der Abbildungen 22 beziehungsweise 24 verhalten sich wie 1: √(3) ≈ 1:1.732.

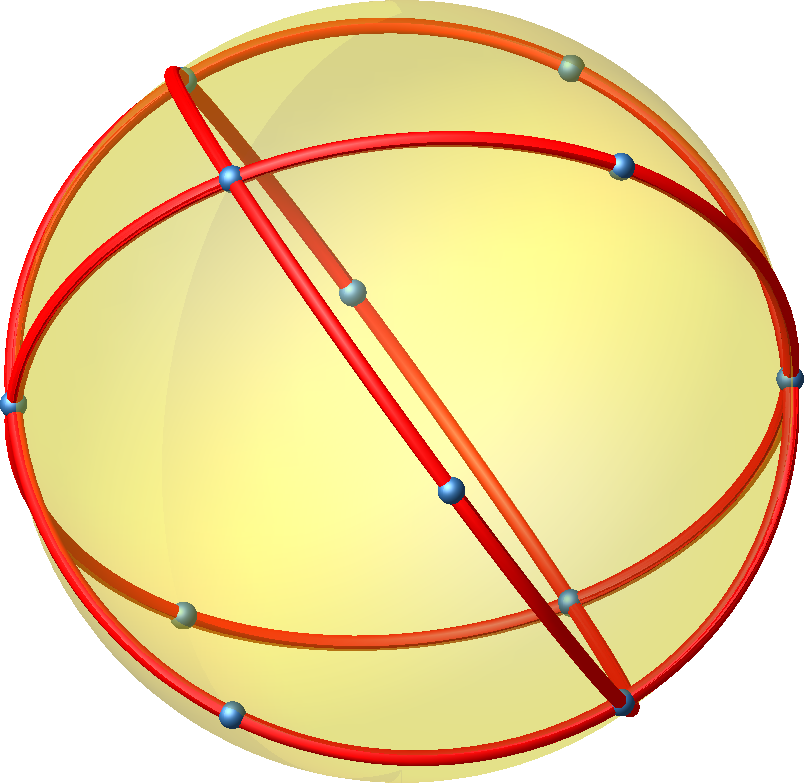
Abb. 25: Auf Umkugel

Weblink

Hans Walser: Gleichseitiges Zwölfeck

http://www.walser-h-m.ch/hans/Miniaturen/G/Gleichseitiges_Zwoelfeck/Gleichseitiges_Zwoelfeck.html

Hans Walser: Sphärische platonische Körper

http://www.walser-h-m.ch/hans/Miniaturen/S/Sphaer_platon_Koerper/Sphaer_platon_Koerper.html

Hans Walser: Torsion

http://www.walser-h-m.ch/hans/Miniaturen/T/Torsion/Torsion.html