Hans Walser, [20141109]
Gleitgelenkmodelle
1 Worum geht es?
Es werden Gleitgelenkmodelle fŸr regelmŠ§ige Vielecke ungerader Eckenzahl konstruiert.
2 Die Bauteile
Wir arbeiten mit zwei Bauteilen: Einheitsstrecken und Einheitsstrecken kombiniert mit einer Gleitnut (Abb. 1).
Abb. 1: Bauteile
Die Gleitnut muss ãgenŸgend langÒ sein.
Die Bauteile sind aus Pappe (Deckel von Ringheftern) geschnitten. Breite 2cm, EinheitslŠnge 8cm. Die Einheitsstrecke als Bauteil ist daher 10cm lang. Lochung etwa 3.5mm, mit Lederlochzange.
Als Bolzen werden MustertŸtenklammern verwendet.
3 Dreieck
FŸr das regelmŠ§ige Dreieck genŸgen drei Einheitsstrecken (Abb. 2).
Abb. 2: Dreieck
4 EiffeltŸrme
FŸr
ungerade Eckenzahlen grš§er als drei arbeiten wir zunŠchst mit einem GerŸst aus
einem gleichschenkligen Dreieck (Abb. 3). FŸr die Eckenzahl 
benštigen
wir zwei Bauteile mit einer Nut und 
Einheitsstrecken. Zusammen mit den
Einheitsstrecken auf den Nut-Bauteilen sind es also insgesamt u Einheitstrecken.
Abb. 3: EiffeltŸrme
Aus den u Einheitsstrecken bauen wir einen Zickzack-Weg, der oben an der Spitze beginnt und schlie§lich wieder dahin zurŸckfŸhrt. Dann ergibt sich an der Spitze automatisch ein Winkel von 180¡/u (Walser 1988). Die Figur erinnert an einen Pylon und insbesondere an den Eiffelturm.
Im Sonderfall u = 5 (Abb. 3a) stellt sich auf den beiden Schenkeln automatisch der Goldene Schnitt ein. †ber den Goldenen Schnitt siehe (Walser 2013).
Die Abbildung 4 zeigt die EiffeltŸrme fŸr u = 9, 11, 13.
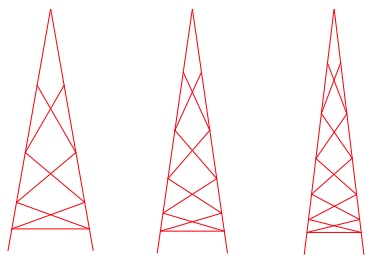
Abb. 4: EiffeltŸrme
5 Ausbau zu Vielecken
Die EiffeltŸrme kšnnen nun mit zusŠtzlichen Einheitsstrecken zu regelmŠ§igen Vielecken ausgebaut werden (Abb. 5).
Abb. 5: Ausbau zum regelmŠ§igen Vieleck
Beim FŸnfeck benštigen wir vier zusŠtzliche Einheitsstrecken, beim Siebeneck 8 zusŠtzliche Einheitsstrecken.
Die Abbildung 6 zeigt die Situation fŸr das 19-Eck. Wir benštigen 80 zusŠtzliche Einheitsstrecken.
Abb. 6: RegelmŠ§iges 19-Eck
Die Tabelle 1 gibt eine †bersicht Ÿber die Anzahl der benštigten Bauteile.
|
n |
u = 2n – 1 |
Eiffelturm |
ErgŠnzung |
Total |
|
2 |
3 |
3 |
0 |
3 |
|
3 |
5 |
5 |
4 |
9 |
|
4 |
7 |
7 |
8 |
15 |
|
5 |
9 |
9 |
16 |
25 |
|
6 |
11 |
11 |
24 |
35 |
|
7 |
13 |
13 |
36 |
49 |
|
8 |
15 |
15 |
48 |
63 |
|
9 |
17 |
17 |
64 |
81 |
|
10 |
19 |
19 |
80 |
99 |
Tab. 1: Benštigte Bauteile
FŸr
ungerades n ist die Totalzahl der
benštigten Bauteile 
. FŸr gerades n
ist die Totalzahl der benštigten Bauteile 
. Wir haben eine ParitŠtsunterscheidung.
Die markierten Zahlen finden wir auch als Diagonalelemente in der eckigen Zahlenspirale der Abbildung 7.
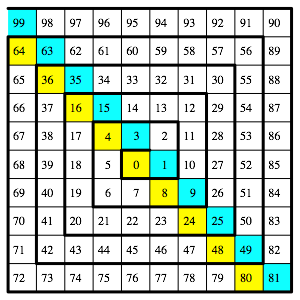
Abb. 7: Eckige Zahlenspirale
6 Sonderfall Siebeneck
Das
Siebeneck lŠsst sich als Sonderfall auch anders gestalten (GŠchter 2013). Wir
kšnnen vier Einheitsstrecken ersetzen durch zwei Strecken der LŠnge 
(Abb. 8).
Abb. 8: Sonderfall Siebeneck
7 Anderer Lšsungsweg
Die Abbildung 9 zeigt einen anderen Lšsungsweg.
Abb. 9: Anderer Lšsungsweg
Beim FŸnfeck sparen wir zwei Einheitsstrecken und einen Bolzen.
Beim Siebeneck sparen wir vier Bauteile und zwei Bolzen.
FŸr Vielecke hšherer Eckenzahl habe ich die Sache nicht untersucht.
Literatur
GŠchter, Albert A. (2013): 7 Zahnstocher. Anregungen fŸr den Mathematikunterricht. St. Gallen: Mefi-Verlag GŠchter. ISBN 978-3-9523962-2-3.
Walser, H. (1988): Ein Schliessungssatz der Elementargeometrie. Elemente der Mathematik (43), 161-169.
Walser, H. (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing Ÿber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.