Hans Walser, [20080318a]

Gleichseitig-rechtwinklige Polygone im Raum

Anregung: Chr. W.

1        Worum es geht

Zu jedem  gibt es ein gleichseitig-rechtwinkliges Polygon im Raum, welches nicht eben ist. Gezeigt werden mšgliche Lšsungen; es gibt viele andere Lšsungen.

2        Was nicht geht

Ein gleichseitiges Dreieck muss das regulŠre Dreieck sein, seine Winkel sind .

Die einzige Mšglichkeit eines gleichseitig-rechtwinkligen Viereckes ist das Quadrat, welches eben ist.

Nach einem Satz von van der Waerden ist ein gleichseitig-gleichwinkliges FŸnfeck zwangslŠufig das ebene regulŠre FŸnfeck mit Winkeln von  (vgl. [van der Waerden 1970], [LŸssy/Trost 1970], [Irminger 1970]). Rechtwinklig ist also nicht mšglich.

3        Gerade Eckenzahl

Die Figur zeigt zunŠchst mšgliche Lšsungen fŸr  und .

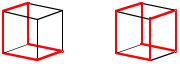
Gleichseitig-rechtwinkliges Sechseck und Achteck

FŸr gerade Eckenzahlen  gibt es ein einheitliches Verfahren, ein gleichseitig-rechtwinkliges Polygon in ein WŸrfelraster einzubetten.

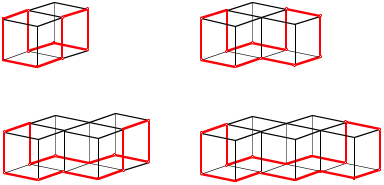
Gleichseitig-rechtwinklige Polygone mit Eckenzahlen 10, 12, 14, 16

4        Ungerade Eckenzahl

4.1      Siebeneck

Das Siebeneck ist speziell. Die Foto zeigt ein Modell. Die Leserin mache sich klar, dass da nichts ãgemurkstÒ ist.

Gleichseitig-rechtwinkliges Siebeneck

Wer meinen mechanischen FŠhigkeiten nicht traut – hier die Eckpunktskoordinaten:

 

 

 

 

 

 

 

 

 

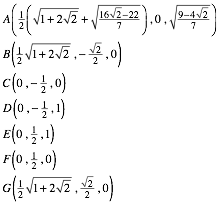
Diese Eckpunktskoordinaten sind mit Zirkel und Lineal konstruierbar, was fŸr das ebene regulŠre Siebeneck nicht mšglich ist.

Im Vergleich mit dem EinheitswŸrfel sieht das Beispiel so aus:

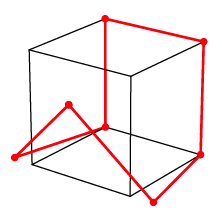
Siebeneck und WŸrfel

4.2      Ungerade Eckenzahl > 7

FŸr ungerade Eckenzahlen grš§er als 7 gibt es ein einheitliches Verfahren, ein Polygon in ein WŸrfelraster einzubetten, bei welchem am Schluss noch ein Zelt angebaut wird.

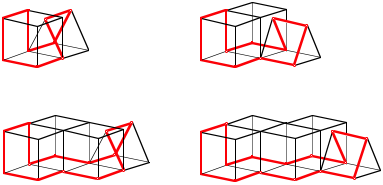
Gleichseitig-rechtwinklige Polygone mit Eckenzahlen 9, 11, 13, 15

Als Stimmungsbild eine Modellfoto fŸr die Eckenzahl 13.

Gleichseitig-rechtwinkliges 13-Eck

Literatur

[Irminger 1970]               Irminger, H.: Zu einem Satz Ÿber rŠumliche FŸnfecke. Elemente der Mathematik. Band 25, 1970, S. 135-136

[LŸssy/Trost 1970]          LŸssy, W. und E. Trost: Zu einem Satz Ÿber rŠumliche FŸnfecke. Elemente der Mathematik. Band 25, Heft 4,
10. Juli 1970, S. 82-83

[van der Waerden 1970]  Van der Waerden, B. L.: Ein Satz Ÿber rŠumliche FŸnfecke. Elemente der Mathematik. Band 25, Heft 4, 10. Juli 1970,
S. 73-78