Hans Walser, [20130620]
Gleichschenklige Trisektrix-Dreiecke
Ausarbeitung einer Idee von H. M.-S., V.
1 Trisektrix von MacLaurin
Die beiden Dreieckspunkte A und B seien fest vorgegeben. Der dritte Dreieckspunkt C soll so gewŠhlt werden, dass die entstehenden Dreiecke ABC die Gleichung
erfŸllen.
Die Trisektrix ist die Ortskurve des Punktes C.
Die Abbildung 1 zeigt die Trisektrix mit einem allgemeinen Trisektrix-Dreieck.
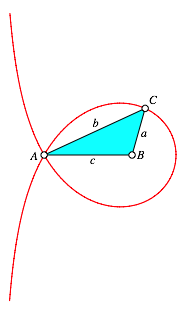
Abb. 1: Trisektrix
FŸr Punkte C auf der Tropfenschleife gilt in der Bedingung das Plus-Zeichen, au§erhalb der Tropfenschleife das Minuszeichen.
FŸr einen
Punkt C auf der Tropfenschleife bedeutet
die Bedingung 
, dass das Quadrat Ÿber c
flŠchengleich ist mit der Vereinigung des Quadrates Ÿber a und dem Rechteck Ÿber b
mit der zweiten Seite a.
2 Winkelhalbierende
Die Winkelhalbierende 
unterteilt die Seite
c in die Abschnitte (Abb. 2):
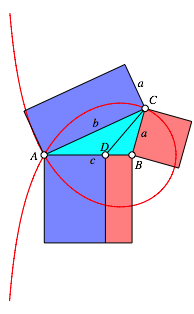
Abb. 2: Winkelhalbierende
FŸr das
rote Hochkant-Rechteck mit der Hšhe c
erhalten wir wegen 
den
FlŠcheninhalt:
Das blaue Hochkant-Rechteck hat den FlŠcheninhalt:
Somit haben gleichfarbige Rechtecke in der Abbildung 2 den gleichen FlŠcheninhalt. Die Situation erinnert an den Kathetensatz.
FŸr einen Punkt C au§erhalb der Tropfenschleife gilt ein analoger Sachverhalt, der aber mit der Šu§eren Winkelhalbierenden und Subtraktionen von FlŠchen arbeitet.
3 Gleichschenklige Trisektrix-Dreiecke
Wir
fragen nun speziell nach gleichschenkligen Dreiecken, die der Bedingung 
genŸgen.
(i) FŸr a = b ergibt sich das rechtwinklige gleichschenklige Dreieck Ÿber c (Abb. 3).
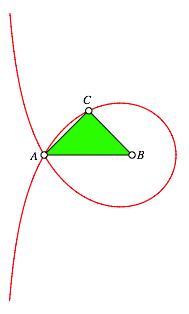
Abb. 3: Rechtwinklig gleichschenkliges Dreieck
(ii) FŸr a = c wird b = 0.
(iii) FŸr
b = c erhalten wir aus 
die Beziehung: 
. Dabei bedeutet 
den Goldenen
Schnitt 
. †ber den Goldenen Schnitt siehe (Walser 2013). Die
Abbildung 4 illustriert die Situation. Das Dreieck wird als Spitzes Goldenes Dreieck bezeichnet.
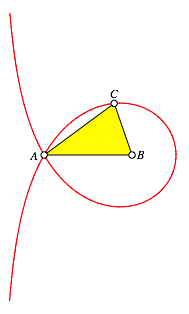
Abb. 4: Spitzes Goldenes Dreieck
(iiii)
Ebenfalls fŸr b = c ergibt sich aus 
die Beziehung 
. Wir erhalten das so genannte Stumpfe Goldene Dreieck (Abb. 5).
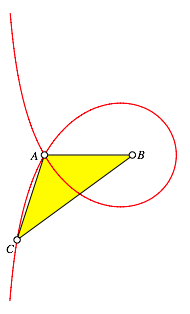
Abb. 5: Stumpfes Goldenes Dreieck
Damit sind alle gleichschenkligen Dreiecke in unserem Kontext besprochen.
4 Nochmals die Winkelhalbierende
FŸr den Fall des rechtwinklig gleichschenkligen Dreieckes fŠllt die Winkelhalbierende mit der Hšhe zusammen und wir erhalten den Satz des Pythagoras und den zugehšrigen Kathetensatz.
Bei den Goldenen Dreiecken teilt die Winkelhalbierende die Gegenseite innen und au§en im VerhŠltnis des Goldenen Schnittes.
Im Spitzen Goldenen Dreieck ergibt sich die Situation der Abbildung 6, wobei wir c = 1 setzen. Die beiden blauen Rechtecke sind sogar kongruent. Es handelt sich dabei um so genannte Goldene Rechtecke.
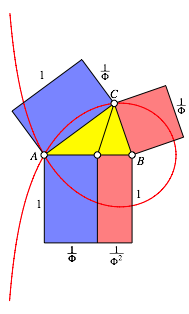
Abb. 6: Unterteilung
Im stumpfen Goldenen Dreieck mŸssen wir mit der Šu§eren Winkelhalbierenden arbeiten. Die Situation ist so vertrackt, dass wir drei Abbildungen benštigen (Abb. 7-9).
Die blauen Rechtecke sind wiederum kongruente Goldene Rechtecke.
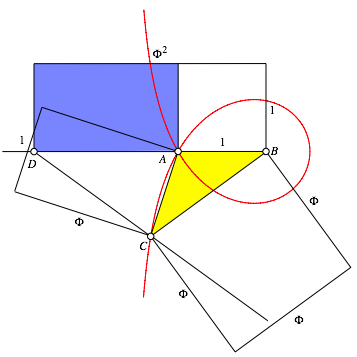
Abb. 7: Blau zum ersten
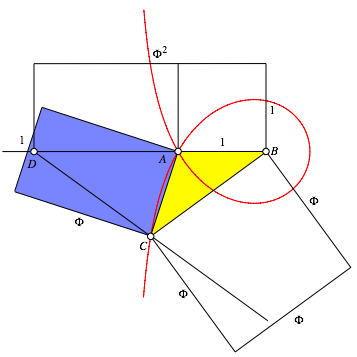
Abb. 8: Blau zum zweiten
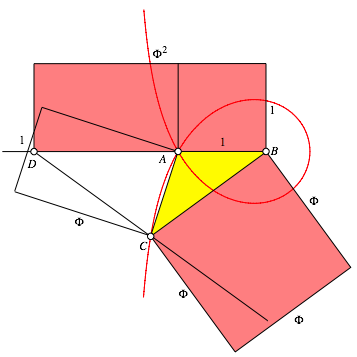
Abb. 9: Rot gleich Rot
Die roten Teile sind eine Vergrš§erung der entsprechenden roten Teile der Abbildung 6.
5 Bemerkung
Bei den Trisektrix-Dreiecken gilt auch eine schšne Winkeleigenschaft (Ohne Beweis, siehe Abb. 10).
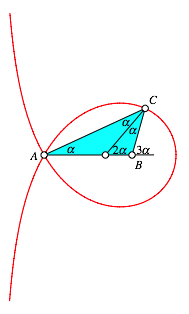
Abb. 10: Winkeleigenschaft
Damit kann die Trisektrix zur Winkeldrittelung verwendet werden. Der zu Drittelnde Winkel muss bei B eingepasst werden.
Daher der Name Trisektrix.
Literatur
Walser, Hans (6. Auflage). (2013). Der Goldene Schnitt. Mit einem Beitrag von Hans Wu§ing Ÿber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.