Hans Walser, [20161022]

Gnomonische Zylinderprojektion

1     Geometrische Idee

Vom Kugelmittelpunkt aus wird zentral auf einen am €quator berźhrenden Zylinder projiziert.

Die Abbildung 1 zeigt exemplarisch die Projektion des Punktes (60ˇN / 60ˇE) von der Kugel auf den Zylinder

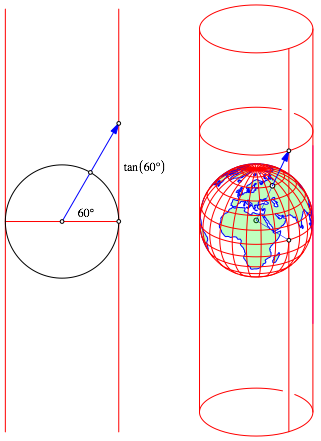
Abb. 1: Gnomonische Zylinderprojektion

Der Zylinder ist oben und unten bei tan(±75ˇ) abgeschnitten. Der Zylinder wird sehr hoch, die Karte ist daher unpraktisch.

Die Abbildung 2 zeigt den abgewickelten Zylindermantel, also die Karte gemŠ§ der gnomonischen Zylinderprojektion. Die Karte ist auf ein Quadrat zugeschnitten. Sie ist bei den geografischen Breiten ± 72.3432ˇ abgeschnitten

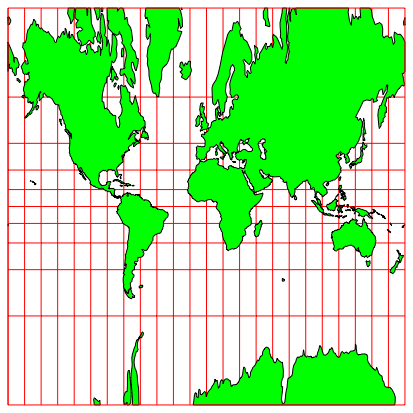
Abb. 2: Gnomonische Zylinderprojektion

 

2     Formeln

Mit  und  bezeichnen wir geografische Breite und LŠnge auf der Kugel, mit u und v die kartesischen Koordinaten in der Ebene. Es gilt:

 

                                                                                                                 (1)

 

3     Vergleiche

3.1    Plattkarte

Formeln:

 

                                                                                                                         (2)

 

 

Gradnetz mit Gitterabstand 15ˇ. Das Gradnetz geht bis zu den Polen.

Abb. 3: Gradnetz der Plattkarte

3.2    Mercator-Karte

Formeln:

 

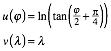                                                                                                     (3)

 

 

Gradnetz mit Gitterabstand 15ˇ. Das Gradnetz geht bis ±75ˇ.

Abb. 4: Gradnetz der Mercator-Karte (oben und unten beschnitten)

3.3    Gnomonische Zylinderprojektion

Formeln siehe (1). Gradnetz mit Gitterabstand 15ˇ. Das Gradnetz geht bis ±75ˇ.

Abb. 5: Gradnetz der gnomonischen Projektion (oben und unten beschnitten)

Wir sehen, dass die Karte der gnomonischen Projektion kein handliches Format hat.

3.4    Mercator-Karte und gnomonische Zylinderprojektion

Die Abbildung 6 zeigt eine Gegenźberstellung von Mercator-Karte (links) und gnomonischer Zylinderprojektion (rechts).

Beide Karten sind auf quadratisches Format zugeschnitten. Bei der Mercator-Karte verlaufen die Schnittlinien auf den geografischen Breiten ± 85.0511ˇ, bei der gnomonischen Zylinderprojektion bereits auf den geografischen Breiten ± 72.3432ˇ. Die Mercator hat also eine grš§ere DarstellungskapazitŠt.

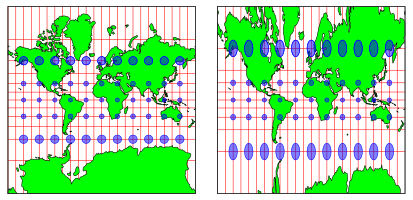
Abb. 6: Mercator-Karte und gnomonische Zylinderprojektion

In beiden Karten sind die Verzerrungsellipsen eingetragen. In der Mercator-Karte sind dies Kreise, da die Mercator-Karte konform (winkeltreu) ist. In der gnomonischen Zylinderprojektion haben wir starke Verzerrungen in Sźd-Nord-Richtung.

 

Websites

Kartenprojektion (24.10.2016):

http://swai.ethz.ch/swaie/MapProjector/MapProjector.de.html