Hans Walser, [20080111b]

Go West, Young Man

Ein Explorer konstruiert einen Polygonzug, indem er jeweils genau nach Westen visiert und auf der Visierlinie immer dieselbe Strecke a abtrŠgt.

Wohin gelangt er schlie§lich?

Bearbeitung

Der Explorer bewegt sich nicht auf einen Breitenkreis.

Die folgenden †berlegungen gelten fŸr einen Startpunkt  auf der nšrdlichen Halbkugel. Wenn der Explorer jeweils genau nach Westen visiert und auf der Visierlinie eine Strecke c abtrŠgt, liegt diese Strecke auf einem Gro§kreis mit dem nšrdlichsten Punkt im Standort des Explorers. Der Explorer bewegt sich sukzessive nach SŸden und nŠhert sich dem €quator. Der sphŠrische Polygonzug ist aus Gro§kreisbšgen zusammengesetzt.

FŸr den Schritt von  auf  rechnen wir im sphŠrischen Dreieck mit diesen beiden Punkten und dem Nordpol.

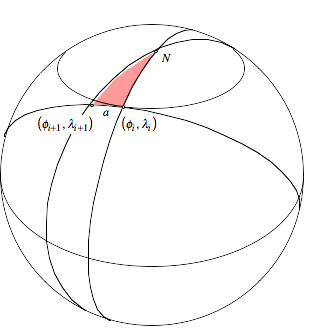
Schritt

Dieses Dreieck ist rechtwinklig an der Ecke  des aktuellen Standortes des Explorers. Die eine Kathete ist a, die andere die Poldistanz . Somit folgt aus dem ãsphŠrischen PythagorasÒ:

FŸr den Winkel  am Nordpol erhalten wir aus dem Seiten-Kosinus-Satz:

Also:

Das Minuszeichen darum, weil unser junger Mann westwŠrts geht.

Damit kšnnen wir die Eckpunkte des sphŠrischen Polygonzuges rekursiv berechnen.

Beispiele

ZunŠchst ein Beispiel auf der Einheitskugel. FŸr ,  und einer Kantenzahl  ergibt sich nachfolgendes Bild.

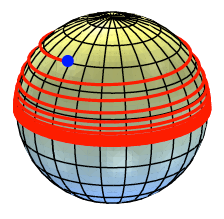
a = 0.1, n = 1000

Wir sehen, wie die Kurve asymptotisch gegen den €quator lŠuft.

Das Beispiel ist allerdings nicht realistisch, weil a viel zu gro§ ist; die Visierlinie wŸrde durch die ErdkrŸmmung unterbrochen. Bei einer Instrumentenhšhe von einem Meter haben wir einen Horizont von ca. 3.5 km. Wenn auch das Empfangsinstrument ein Meter Ÿber Boden ist, kšnnen wir mit einer Visierdistanz von max. 7 km arbeiten.

Einer Visierdistanz von 6.366 km entspricht auf der Einheitskugel . Im folgenden Beispiel ist ,  und  (wow!).

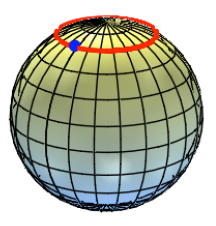
a = 0.001, n = 3141

Das sieht jetzt so aus, wie wenn unser junger Mann genau auf dem Breitenkreis um die Erde herumgegangen ist. In Wirklichkeit befindet er sich aber nach dem ersten Umgang etwa 17 km sŸdlich des Ausgangspunktes.