Hans Walser, [20190421]
Goldberg
Idee: Patrik
G. K. Wiesner, BSc ETHZ, Davidgasse 42, A - 1100 Wien
1 Worum geht es?
Beispiel
einer Zerlegungsgleichheit eines gleichseitigen Dreieckes und eines regelm§igen
Fnfeckes (Abb. 1) nach Michael Goldberg (1952). Die Zerlegung bentigt sechs
Teile. Kinematische Realisierung.
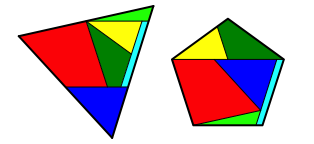
Abb. 1: Dreieck und regelm§iges Fnfeck
2 Daten
Wir
normieren die Flchen der beiden Polygone auf 1.
Fr die
Seitenlnge ![]() des Dreieckes erhalten wir damit:
des Dreieckes erhalten wir damit:
![]() (1)
(1)
Fr die
Seitenlnge ![]() des Fnfeckes erhalten wir:
des Fnfeckes erhalten wir:
![]() (2)
(2)
Das
Seitenverhltnis ist:
![]() (3)
(3)
Die
Seitenlnge des Dreieckes ist also fast doppelt so gro§ wie jene des Fnfeckes.
Allerdings darf man nicht mit dem Nherungswert 2 arbeiten, weil sonst die Zerlegung
sichtbar ungenau wird (eigene Erfahrung).
3 Konstruktives Vorgehen
Wir
beginnen mit dem regelm§igen Fnfeck und zeichnen die horizontale Diagonale
(Abb. 2a).
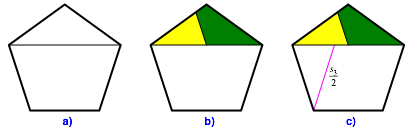
Abb. 2: Erste drei Schritte
Durch den
Mittelpunkt dieser Diagonalen zeichnen wir eine Parallele zur linken Topfseite
des Fnfeckes (Abb. 2b). Somit erhalten wir das gelbe und das dunkelgrne
Teilstck.
Bis jetzt
haben wir uns ausschlie§lich in der Fnfeckgeometrie bewegt.
Nun kommt
das Dreieck ins Spiel.
Wir tragen
von der linken unteren Ecke des Fnfeckes aus die halbe Dreieckseite auf die
Diagonale ab (Abb. 2c). Wegen (3) ist die entstehende Strecke (magenta) nicht parallel zur rechten
Topfseite des Fnfeckes.
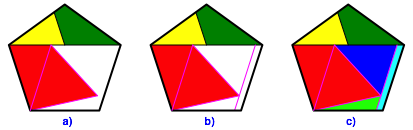
Abb. 3: Fortsetzung der Konstruktion
Die
magenta Strecke ergnzen wir zum gleichseitigen Dreieck (Abb. 3a). So erhalten
wir das rote Viereck.
Durch die
Spitze des gleichseitigen Dreiecks zeichnen wir eine Parallele zur magenta
Strecke (Abb. 3b). Wir haben an dieser Spitze jetzt drei Winkel von 60¡. Diese
werden in die Ecken des gleichseitigen Dreiecks kommen.
Wir knnen
nun noch das dunkelblaue und das hellgrne Dreieck sowie das hellblaue
Viereck markieren. Das hellblaue Viereck ist dem Anschein zum Trotz kein
Parallelogramm. Lediglich bei beiden kurzen Seiten sind parallel.
Die sechs
Teile knnen nun gem§ Abbildung 1 ins gleichseitige Dreieck eingepasst werden.
4 Orientierungen
In der Abbildung
4 ist im Fnfeck zustzlich zu den Farben eine senkrechte Schraffur angebracht
worden.
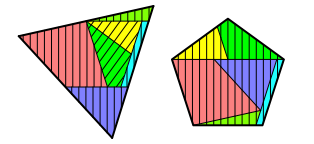
Abb. 4: Orientierungen
Die Teile
werden nun unter Beibehaltung der Schraffur ins Dreieck eingepasst. Bei den
Teilen, die sich im Fnfeck unterhalb der Diagonale befinden, ist die Schraffur
nach wie vor senkrecht. Diese Teile werden also entweder verschoben (dunkelblau
und hellgrn) oder um 180¡ gedreht (rot und himmelblau). Bei den beiden Teilen
oberhalb der Fnfeckdiagonale (gelb und grn) kommt noch eine Verdrehung um ein
Vielfaches von 36¡ dazu.
5 Kinematisches Modell
Der
bergang vom Fnfeck zum Dreieck und zurck lsst sich durch ein kinematisches
Modell visualisieren. Dieses Modell geht auf Patrik G. K. Wiesner,
BSc ETHZ, Davidgasse 42, A - 1100 Wien, zurck und ist patentiert.
Die
Abbildung 5 zeigt die Startposition des Fnfeckes. Die beiden blauen, der gelbe
und der grne Punkt sind ortsfeste Drehpunkte. Die beiden roten Punkte sind
Gelenkpunkte. Sie bilden zusammen mit den beiden blauen Punkten ein
Parallelogramm. An den Parallelogrammseiten sind der Reihe nach das
hellblaue, das dunkelblaue, das rote und das hellgrne Teilstck befestigt. Sie
drehen mit diesen Seiten. Im Detail hei§t das, dass das hellgrne Dreieck ortsfest
bleibt, das hellblaue und das hellrote Viereck je um einen blauen Punkt
drehen und das dunkelblaue Dreieck unter Beibehaltung der Orientierung (also
ohne Verdrehen) herumschaukelt.
Das gelbe
Dreieck dreht um den gelben Punkt, und zwar gegengleich zum Parallelogramm und
nur mit einem Fnftel der Drehgeschwindigkeit.
Das
dunkelgrne Viereck dreht um den dunkelgrnen Punkt im gleichen Sinn wie das
Parallelogramm, aber nur mit vier Fnfteln der Drehgeschwindigkeit.
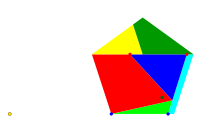
Abb. 5: Startposition
Die
Abbildung 6 zeigt den kinematischen Prozess in Schritten von 30¡.
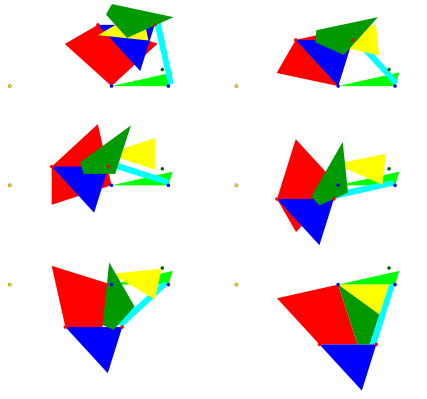
Abb. 6: Kinematik
Auf meiner
Homepage findet sich eine GeoGebra-Animation (Animation3) dazu. Der Prozess
geht hin und zurck. Man kann ihn auch endlos vorwrts laufen lassen, wegen der
unterschiedlichen Drehgeschwindigkeiten dauert es dann ein bisschen, bis die
Startposition wieder erreicht ist (Animation4).
Weitere Animationen
hier.
Wie lsst
sich dies mechanisch realisieren?
Weblinks
DITOH,
Spezieller platonischer Krper
Animationen
https://www.ditoh.com/dr-hans-walser-ethz-uni-basel
Hans
Walser: Dudeney
http://www.walser-h-m.ch/hans/Miniaturen/D/Dudeney/Dudeney.htm
Hans
Walser: Dudeney
http://www.walser-h-m.ch/hans/Miniaturen/D/Dudeney2/Dudeney2.htm
Hans
Walser: Quadrat und Fnfeck
www.walser-h-m.ch/hans/Miniaturen/Q/Quadrat_u_Fuenfeck/Quadrat_u_Fuenfeck.htm