Hans Walser, [20200608]
Goldene Doppelspirale
1 Worum geht es?
Aus gleichseitigen Dreiecken konstruierte Doppelspirale (Abb. 1) mit einem LŠngenverkleinerungsfaktor im Umfeld des Goldenen Schnittes.
2 Die Doppelspirale

Abb. 1: Goldene Doppelspirale
Das Au§enprofil der einen Spirale berźhrt das Innenprofil der anderen und umgekehrt. Die beiden Spiralen sind punktsymmetrisch.
3 LŠngen-Verkleinerungsfaktor
Wir berechnen den LŠngen-Verkleinerungsfaktor f beim †bergang von einem Dreieck zum nachfolgenden (Abb. 2).
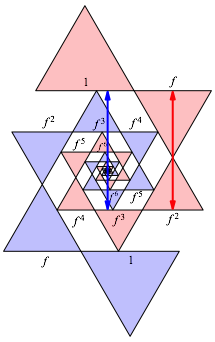
Abb.2: Verma§ung
Aus der Abbildung 2 lesen wir ab:
![]() (1)
(1)
Diese Gleichung sechsten Grades lŠsst sich mit schulischen Mitteln einfach lšsen. Da die triviale Lšsung f = 0 fźr uns nicht relevant ist, kšnnen wir (1) durch f dividieren und vereinfachen zu:
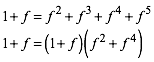 (2)
(2)
Eine weitere Lšsung ist somit f = –1. Diese ist fźr uns ebenfalls nicht relevant, sodass wir durch den entsprechenden Linearfaktor dividieren kšnnen. Dies ergibt:
![]() (3)
(3)
Aus dieser biquadratischen Gleichung ergibt sich:
![]() (4)
(4)
Fźr reelle Lšsungen fźr f ist in (4) nur die Plus-Lšsung relevant. Mit der Schreibweise des Goldenen Schnittes (Walser 2013)
![]() (5)
(5)
ist also:
![]() (6)
(6)
Wiederum ist nur die positive Lšsung relevant, so dass wir schlie§lich haben:
![]() (7)
(7)
Dies rechtfertigt die Bezeichnung Goldene Doppelspirale.
Literatur
Walser, H. (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing źber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.
Websites
Hans Walser: Goldene Spirale
www.walser-h-m.ch/hans/Miniaturen/G/Goldene_Spirale/Goldene_Spirale.htm
Hans Walser: Goldene Spiralen
www.walser-h-m.ch/hans/Miniaturen/G/Goldene_Spiralen/Goldene_Spiralen.pdf
Hans Walser: Berźhrspiralen
www.walser-h-m.ch/hans/Miniaturen/B/Beruehrspiralen/Beruehrspiralen.htm
Hans Walser: Hexenspirale
www.walser-h-m.ch/hans/Miniaturen/H/Hexenspirale2/Hexenspirale2.htm