1 Worum geht es?

Spiel mit Krümmungskreisen und einer speziellen Ellipse.

2 Konstruktion der Ellipse

Wir beginnen mit fünf nebeneinander liegenden Kreisen (Abb. 1).

Abb. 1: Fünf Kreise

Wir legen eine Ellipse darum so, dass die beiden äußersten Kreise die Krümmungskreise an den spitzen Scheiteln der Ellipse sind (Abb. 2).

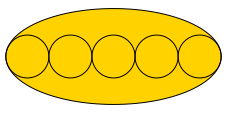
Abb. 2: Ellipse

Wenn wir den Kreisradius auf 1 setzen, ergibt sich für die Ellipse die lange Halbachse 5 und die kurze Halbachse √5.

3 Der Goldene Schnitt

Die kurze Halbachse wird durch den mittleren Kreis im Verhältnis des Goldenen Schnittes unterteilt, und zwar in der Reihenfolge Minor-Major-Minor (Abb. 3). Nachweis rechnerisch.

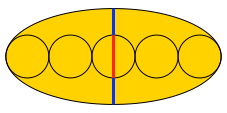
Abb. 3: Der Goldene Schnitt

4 Fünf goldene Ellipsen

Wir stapeln nun fünf goldene Ellipsen aufeinander (Abb. 4).

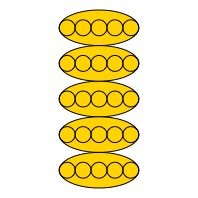
Abb. 4: Fünf goldene Ellipsen

Der Krümmungskreis im oberen stumpfen Scheitel der obersten Ellipse ist auch der Krümmungskreis im unteren stumpfen Scheitel der untersten Ellipse (Abb. 5).

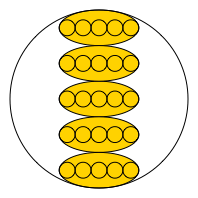
Abb. 5: Krümmungskreis

5 Der goldene Schnitt zum zweiten

Auch hier finden wir den goldenen Schnitt, wiederum in der Reihenfolge Minor-Major-Minor (Abb. 6). Nachweis rechnerisch

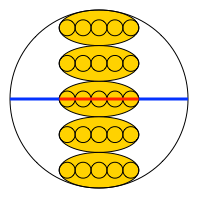
Abb. 6: Der goldene Schnitt

Weblinks

Hans Walser: Kreise und Ellipsen

http://www.walser-h-m.ch/hans/Miniaturen/K/Kreise_u_Ellipsen3/Kreise_u_Ellipsen3.html

Hans Walser: Kreise und Ellipsen

http://www.walser-h-m.ch/hans/Miniaturen/K/Kreise_u_Ellipsen2/Kreise_u_Ellipsen2.html

Hans Walser: Ellipsen im DIN-Format

http://www.walser-h-m.ch/hans/Miniaturen/E/Ellipsen_DIN/Ellipsen_DIN.htm

Hans Walser: Kreise und Ellipsen

http://www.walser-h-m.ch/hans/Miniaturen/K/Kreise_u_Ellipsen/Kreise_u_Ellipsen.htm

Hans Walser: Minimalellipse

http://www.walser-h-m.ch/hans/Miniaturen/M/Minimalellipse/Minimalellipse.htm

Hans Walser: Orthogonale Großkreise

http://www.walser-h-m.ch/hans/Miniaturen/O/Orth_Grosskreise/Orth_Grosskreise.htm