Hans Walser, [20171112]

Goldene Pyramiden

Anregung: R. Q., W.

1 Worum geht es?

Durch eine geeignete Anordnung von zwei Goldenen Pyramiden kommen wir zum Ikosaeder und zum Dodekaeder.

2 Die Goldene Pyramide

Die Goldene Pyramide hat ein regelmäßiges Fünfeck als Grundfläche und als Seitenflächen fünf gleichschenklige Dreiecke, deren Schenkel zur Basis im Verhältnis des Goldenen Schnittes (Walser 2013) stehen (Abb. 1).

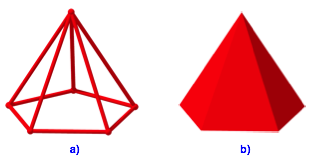
Abb. 1: Goldene Pyramide

Die Abbildung 2 zeigt zwei verschiedene Abwicklungen (Schnittmuster) der Goldenen Pyramide.

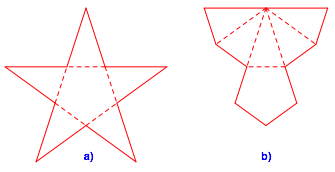
Abb. 2: Schnittmuster der Goldenen Pyramide

3 Es gibt – gibt es?

R. kam etwas verstört von der Schule nach Hause. An sich ging sie gerne in die Schule und liebte ihre Lehrerin.

In der Schule seien die Pyramiden behandelt worden. Ihre Frage, ob es auch Pyramiden mit fünf Seitenflächen gebe, sei verneint worden. Dabei könne sie, R., sich das sehr gut vorstellen.

Nach dem Mittagessen wurde aus Karton mit dem Schnittmuster der Abbildung 2b eine Pyramide wie Abbildung 1a gebaut. R. erklärte, so habe sie sich das vorgestellt und ging damit zur Schule.

Auf Rückfrage sagte sie am Abend, das sei ein Missverständnis gewesen. Die Lehrerin habe die Frage so verstanden, ob auch Pyramiden mit fünf Seitenflächen gebaut worden seien.

Existiert, was man „sich sehr gut vorstellen“ kann?

4 Zweite Goldene Pyramide

Wir fügen der Goldenen Pyramide eine zweite kongruente Pyramide mit selber Achse, aber der Spitze nach unten bei. Dabei soll die zweite Pyramide um die gemeinsame Achse um 36° verdreht sein. Ihr Boden soll die Höhe der ersten Pyramide im Goldenen Schnitt teilen. Der Abstand zwischen den beiden Pyramidenböden sei dabei der Major. Die Abbildung 3 zeigt die Situation.

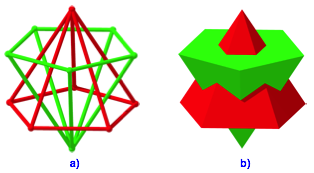
Abb. 3: Zweite Pyramide

Nun gilt folgendes:

· Die konvexe Hülle der Figur ist das reguläre Ikosaeder (Abb. 4).

· Die Schnittfigur der beiden Pyramiden ist das reguläre Dodekaeder (Abb. 5).

Beweise durch Nachrechnen oder Einsicht.

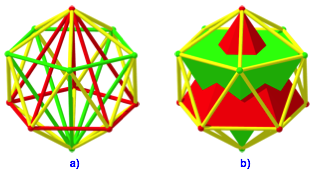
Abb. 4: Konvexe Hülle ein Ikosaeder

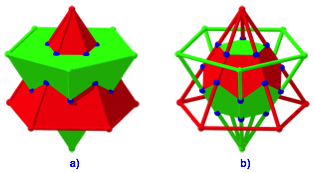
Abb. 5: Schnittfigur ein Dodekaeder

5 Analogie zum Kepler-Stern

Wir fassen ein reguläres Tetraeder als Pyramide auf und setzen zwei kongruente Tetraeder mit umgekehrter Orientierung auf dieselbe Achse. Die beiden Tetraeder sollen um 60° zueinander verdreht sein. Der Pyramidenboden des einen Tetraeders soll die Pyramidenhöhe des anderen halbieren.

Die entstehende Figur ist der Kepler-Stern. Die konvexe Hülle ist der Würfel. Die Schnittfigur der beiden Tetraeder ist das reguläre Oktaeder.

Literatur

Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-937219-85-1.