Hans Walser, [20130528]

Goldene Rechtecke

1        Ausgangslage

Das Einheitsquadrat und das Rechteck mit den SeitenlŠngen  und  sind flŠchengleich.

Unter  verstehen wir den Goldenen Schnitt (Walser 2013):

 

Die Abbildung 1 zeigt die Situation.

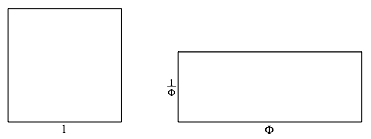
Abb. 1: Quadrat und Rechteck

Das Rechteck hat das SeitenverhŠltnis . Es ist zu unterscheiden vom so genannten Goldenen Rechteck mit dem SeitenverhŠltnis . Ich schlage fŸr unser lŠngeres Rechteck den Namen langes Goldenes Rechteck vor.

2        Zerlegungsgleichheit

Das Quadrat und das lange Goldene Rechteck der Abbildung 1 sind flŠchengleich und somit zerlegungsgleich. Die Abbildung 2 zeigt eine gemeinsame Zerlegung.

Abb. 2: Zerlegungsgleichheit

Wir kommen mit zwei Puzzle-Formen durch. Die entsprechenden Puzzle-Teile kšnnen durch Verschieben zur Deckung gebracht werden.

3        Seitenparallele Rechtecke

Die Frage ist, ob es auch eine gemeinsame Zerlegung in seitenparallele Rechtecke gibt. Die Abbildung 3 zeigt den ersten Schritt dieser gemeinsamen Zerlegung.

Abb. 3: Erster Schritt

Das grš§tmšgliche gemeinsame Puzzle-Teil ist nun ein Goldenes Rechteck. Als Restrechtecke haben wir nun aber links ein langes Goldenes Rechteck und rechts ein Quadrat. Damit ist klar, dass das Zerlegungsverfahren nicht terminiert. Hier Šu§ert sich die IrrationalitŠt des Goldenen Schnittes. Die Abbildung 4 zeigt den nŠchsten Schritt.

Abb. 4: Zweiter Schritt

Das Puzzle-Rechteck ist wiederum ein Goldenes Rechteck. Das Restrechteck links ist nun ein Quadrat und das Restrechteck rechts ein langes Goldenes Rechteck. Die Abbildung 5 zeigt die folgenden Schritte, theoretisch geht es ad infinitum.

Abb. 5: Infinitesimale Ausschšpfung

Bei der Anordnung der Puzzle-Teile gemŠ§ Abbildung 5 kommen wir mit drei Farben aus. Wir kšnnen natŸrlich auch anders anordnen. Die Abbildung 6 zeigt eine spiralfšrmige Anordnung. Wir benštigen vier Farben.

Abb. 6: Spiralfšrmige Anordnung

3.1      Etwas Rechnung

Die Goldenen Rechtecke haben die FlŠcheninhalte:

 

Da sie zusammen das Einheitsquadrat ausschšpfen, erhalten wir die Beziehung:

 

3.2      Entzerrung

Wenn wir das Quadrat der Abbildung 6 in der senkrechten Richtung mit dem Faktor  strecken, erhalten wir ein Goldenes Rechteck im Hochformat, welches von Quadraten ausgeschšpft wird (Abb. 7).

Abb. 7: Goldenes Rechteck

Wenn wir umgekehrt das lange Goldene Rechteck der Abbildung 6 in horizontaler Richtung mit dem Faktor  strecken (also inhaltlich schrumpfen), erhalten wir ein Goldenes Rechteck im Querformat, das durch Quadrate ausgeschšpft wird (Abb. 8).

Abb. 8: Die sattsam bekannte Figur

Literatur

Walser, Hans (6. Auflage). (2013). Der Goldene Schnitt. Mit einem Beitrag von Hans Wu§ing Ÿber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.