Hans Walser, [20140412]

Goldene Spirale

Adaptation der Fibonacci-Spirale von E. J. .

1 Die geometrische Fibonacci-Folge

Mit dem Goldenen Schnitt (Walser, 2013) bauen wir die geometrische Folge:

Diese Folge genügt der Rekursion:

Die Folge ist damit auch eine Fibonacci-Folge. Sie hat die Startwerte 1 und .

Nachweis der Rekursion:

Die Abbildung 1 illustriert die Rekursion mit Pythagoras. Die Angaben beziehen sich auf die Flächeninhalte der Quadrate.

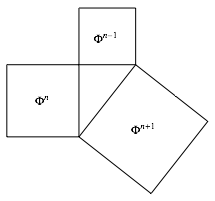
Abb. 1: Pythagoras und der Goldene Schnitt

Das rechtwinklige Dreieck hat das Seitenverhältnis .

2 Die Spirale

Wir bauen die Figur zu einer Spirale aus. Die Abbildung 2 zeigt den Anfang der Spirale.

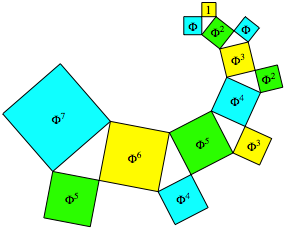
Abb. 2: Spiralenstart

Die Abbildung 3 zeigt einen größeren Ausschnitt.

Abb. 3: Goldene Spirale

Es handelt sich um eine eckige logarithmische Spirale. Das Zentrum lässt sich daher mit Ortsbogen und/oder Apolloniuskreisen konstruieren.

Literatur

Walser, Hans (6. Auflage 2013). Der Goldene Schnitt. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.