Hans Walser, [20201013]
Goldene Trapeze und Goldenes Sechseck
1 Worum geht es?
Es gibt zwei verschiedene gleichschenklige
Trapeze mit den SeitenlŠngen 
, 1, 
und der
DiagonalenlŠnge 
. Die Basiswinkel sind 60ˇ.
Dabei ist 
der
Goldene Schnitt (Walser 2013a). Die DiagonalenlŠnge 
erscheint
auch im Einheitsquadrat und ist die Schlźsselzahl fźr das DIN-Format (Walser
2013b).
Die beiden Goldenen Trapeze kšnnen zum Goldenen Sechseck kombiniert werden.
2 Herleitung und Darstellung der Goldenen Trapeze
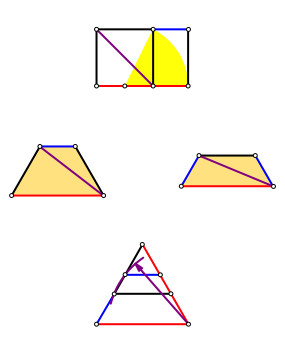
Abb. 1: Ohne Worte noch Formeln
3 Ma§angaben
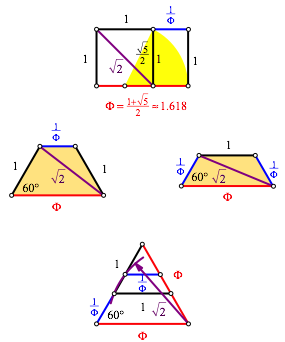
Abb. 2: Ma§angaben
4 Goldenes Sechseck
Die beiden Goldenen Trapeze kšnnen wir zum Goldenen Sechseck zusammengefźgt werden (Abb. 3).
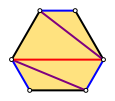
Abb. 3: Goldenes Sechseck
Das Goldene Sechseck hat alternierend die
SeitenlŠngen 1 und 
.
Im Goldenen Sechseck haben die langen
Diagonalen die LŠnge 
und die kurzen
Diagonalen die LŠnge 
(Abb. 4).
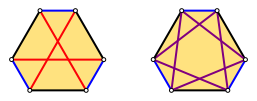
Abb. 4: Lange und kurze Diagonalen im Goldenen Sechseck
Mit dem Goldenen Sechseck allein kann die
Ebene nicht parkettiert werden. Hingegen kšnnen wir mit regelmŠ§igen Sechsecken
der SeitenlŠnge 1 kombinieren (Abb. 5.1) oder mit regelmŠ§igen Sechsecken der
SeitenlŠnge 
(Abb.
5.2).
Abb. 5.1: Gro§es Parkett
Abb. 5.2: Kleines Parkett
Literatur
Walser, Hans (2013a): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing źber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.
Walser, Hans (2013b): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-69-1.