Hans Walser, [20180502]

Goldene Treppe

Idee und Anregung: Hartmut Rehlich, Braunschweig

1     Worum geht es?

Die Goldene Treppe ist ein nicht konvexes Sechseck, das sich in zwei zum Startsechseck Šhnliche, aber nicht kongruente Teilsechsecke zerlegen lŠsst.

Der Goldene Schnitt spielt dabei eine wesentliche Rolle.

2     Die Goldene Treppe

Die Abbildung 1a zeigt die von Hartmut Rehlich entdeckte Figur der Goldenen Treppe.

Abb. 1: Goldene Treppe

Die VerhŠltnisse der SeitenlŠngen lassen sich durch Potenzen von  angeben. Dabei ist  der Goldene Schnitt (Walser 2013):

 

                                                                                                           (1)

 

 

Die SeitenlŠngen bilden eine geometrische Folge mit dem Quotienten . Dabei sind die in der Abbildung 1a horizontalen Seiten ganzzahlige Potenzen von , die vertikalen Seiten echt halbzahlige Potenzen von .

Die Abbildung 1b zeigt die Zerlegung in zwei kleinere Goldene Treppen. Das FlŠchenverhŠltnis der beiden Teilfiguren ist . Es ist daher in Anlehnung an die źbliche Terminologie beim Goldenen Schnitt sinnvoll, die grš§ere Teilfigur als Major und die kleinere als Minor zu bezeichnen.

 

Das grš§ere Teilfigur (Major) ist gleichsinnig Šhnlich zur Ausgangsfigur der Abbildung 1a, das kleinere Teilfigur (Minor) ist ungleichsinnig Šhnlich.

3     Iterationen der Zerlegung

Da die Teilfiguren wiederum Goldene Treppen sind, kšnnen sie ebenfalls je in zwei Goldene Treppen zerlegt werden.

3.1    Zerlegung aller Teilfiguren

Die Abbildung 2 zeigt schrittweise die Zerlegungen.

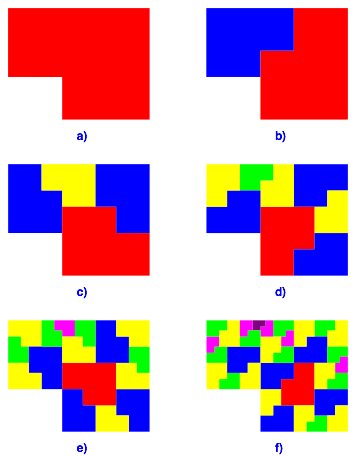
Abb. 2: Zerlegungen

Bei der Abbildung 2c kommen zwei gleich gro§e Teilfiguren vor (blau). Sie sind aber unterschiedlich entstanden. Das eine ist der Minor des Majors der ersten Zerlegung (Abb. 2b), das andere der Major des Minors der ersten Zerlegung.

In der Abbildung 2d haben wir zweimal drei gleich gro§e Teilfiguren (blau und gelb).

Die Tabelle 1 gibt einen †berblick źber die HŠufigkeiten gleich gro§er Teilfiguren. Wir erhalten die Binomialkoeffizienten.

 

 

 

 

 

 

 

 

a)

1

 

 

 

 

 

b)

1

1

 

 

 

 

c)

1

2

1

 

 

 

d)

1

3

3

1

 

 

e)

1

4

6

4

1

 

f)

1

5

10

10

5

1

Tab. 1: HŠufigkeiten

Walser (2017) sowie [2] gibt ein analoges Beispiel zur Visualisierung der Binomialkoeffizienten bei rechtwinkligen Dreiecken.

3.2    Zerlegung des Minors

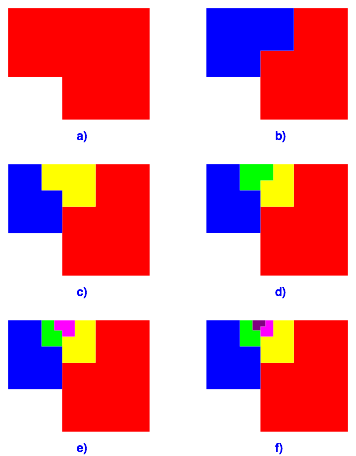
Abb. 3: Zerlegung des Minors

In der Abbildung 3 wird jeweils immer nur der Minor  zerlegt. Wir erhalten einen Grenzpunkt, der die Oberkante im VerhŠltnis des Goldenen Schnittes teilt.

 

3.3    Zerlegung des Majors

Abb. 4: Zerlegung des Majors

Es entsteht eine Spirale. Die Abbildung 5 zeigt die Spirale in einer anderen FŠrbung.

Abb. 5: Spirale

4     Schiefe Treppe

Die Goldene Treppe hat ausschlie§lich rechte Winkel.

Wenn wir bei gleichen SeitenverhŠltnissen mit schiefen Winkeln arbeiten, kšnnen wir nicht in zwei, sondern nur in vier Šhnliche Teilfiguren zerlegen (Abb. 6).

Abb. 6: Schiefe Situation

Zwei dieser Teilfiguren sind kongruent.

 

Literatur

Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing źber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.

Walser, Hans (2017): Rechtwinklige Dreiecke ... . Ideenkiste. ml, mathematik lehren 204 | 2017, 51.

 

Websites

[1] Hans Walser: Zerlegung in Šhnliche Teilfiguren (2.5.2018):

www.walser-h-m.ch/hans/Miniaturen/Z/Zerlegung/Zerlegung.htm

[2] Hans Walser: Dreiecksunterteilung (2.5.2018):

www.walser-h-m.ch/hans/Miniaturen/D/Dreiecksunterteilung2/Dreiecksunterteilung2.htm