Hans Walser, [20220211]

Goldener Baum

1 Worum geht es?

Variationen um das Fraktal des Goldenen Baumes (Walser 2013, S. 20f).

2 Baumfraktal

Bei einem Baumfraktal bleibt die Startfigur durchwegs in Originalgröße erhalten.

3 Beispiele

3.1 Streckenfraktal

Wir beginnen mit einer senkrechten Strecke (Stamm), und setzen schrittweise verkürzte Verästelungen an (Abb. 1 und 2). Bei einer Verästelung setzen wir drei gleiche Winkel (je 120°).

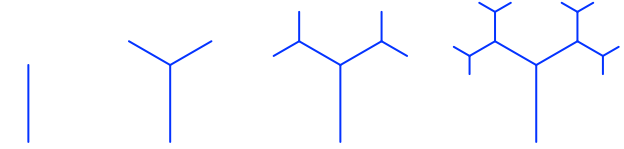
Abb. 1: Wachstum

Abb. 2: Wachsen und Vergehen

Wir können drei Bäume zu einer Figur mit dreistrahliger Drehsymmetrie zusammensetzen (Abb. 3 rechts).

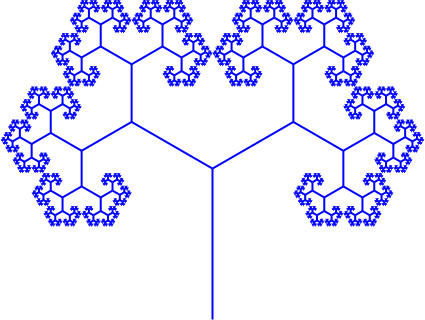
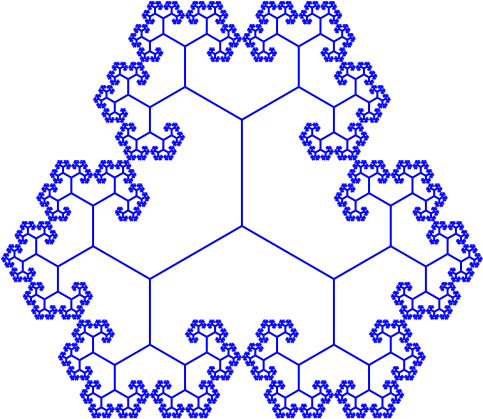
Abb. 3: Berührung im Grenzfall

Der Längenskalierungsfaktor s wurde so gewählt, dass sich im Grenzfall die äußersten Ästen nicht überlappen, aber auch kein Zwischenraum bleibt. Diese Bedingung liefert (Trigonometrie, geometrische Reihe) den Skalierungsfaktor s:

Dies ist der „kleine“ Goldene Schnitt (Walser 2013). Daher der Name Goldener Baum.

In den bisherigen Beispielen waren die Strecken immer gleich breit. Dies ist unnatürlich, werden doch die Äste nach außen immer dünner. In der Abbildung 4 ist dem Rechnung getragen. Das dritte Bild zeigt den Link zum unverdünnten Streckenfraktal (Abb. 1 bis 3).

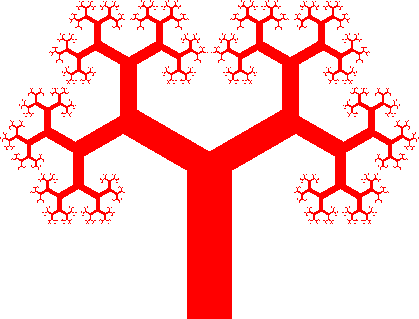
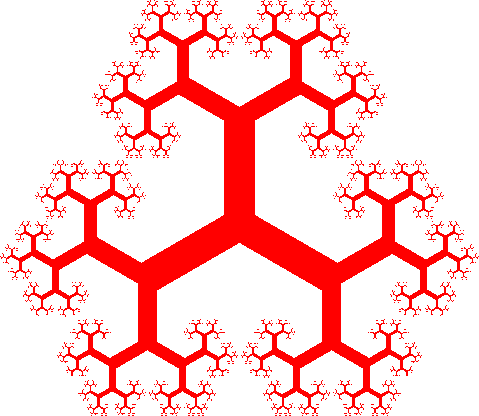
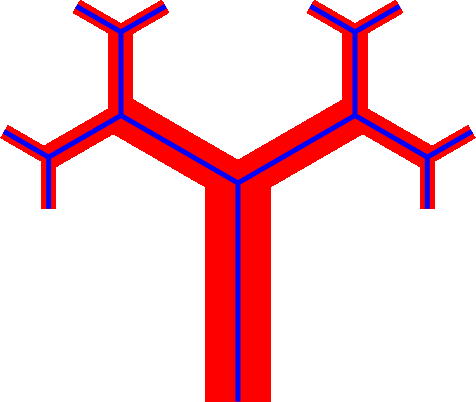
Abb. 4: Die Äste werden immer dünner. Dreierteilung

Wir können die Strecken durch andere, flächige Figuren ersetzen. Damit erübrigt sich auch das Problem der Strichbreite.

3.2 Mit Zweiecken

Die Kreisbogenzweiecke haben Innenwinkel 60°. Daher ergeben sich an den Rändern der Zweiecke durchgezogene Spiralen. Die Abbildung 5 gibt den Baum, die dreiteilige Figur und den Link zum Streckenfraktal (Abb. 1 bis 3) wieder.

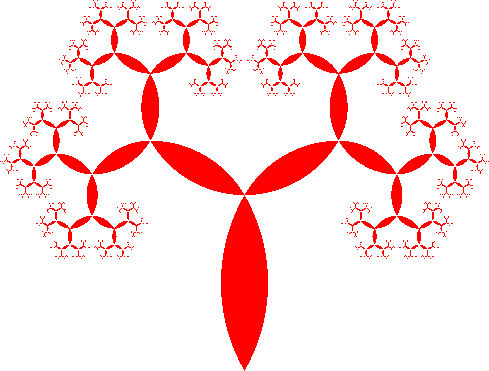
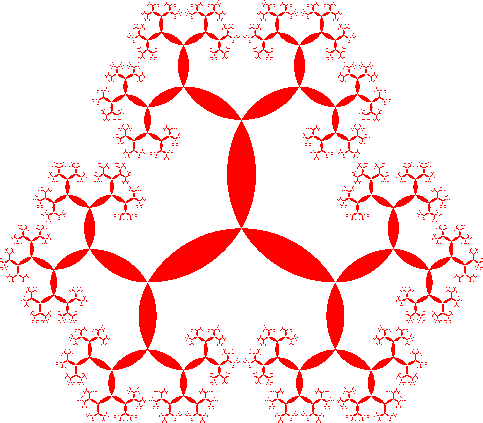
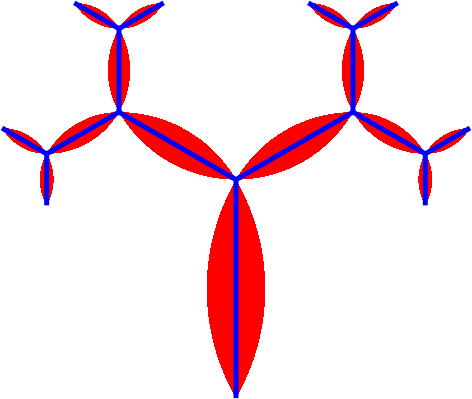
Abb. 5: Zweiecke

3.3 Mit gleichseitigen Dreiecken

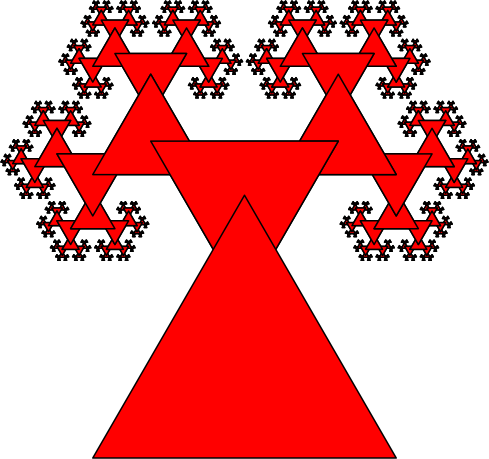
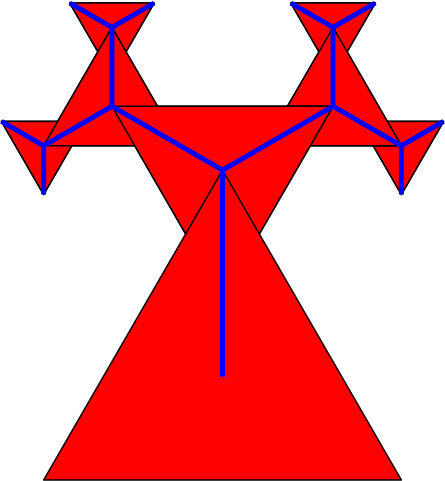
Abb. 6: Gleichseitige Dreiecke

Die Abbildung 7 zeigt eine überlappungsfreie Variante mit gleichseitigen Dreiecken. Bei der dreiteiligen Drehsymmetrie muss im Zentrum ein zusätzliches gleichseitiges Dreieck eingefügt werden.

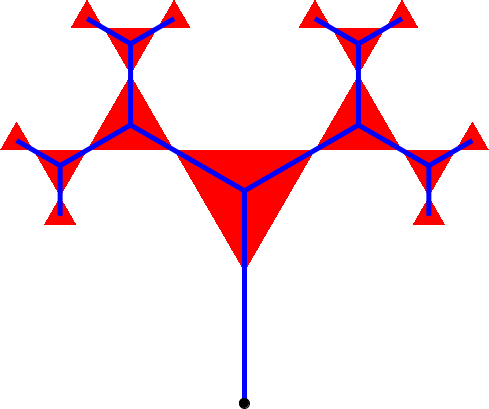
Abb. 7: Gleichseitige Dreiecke

Wir stellen fest, dass bei allen bisherigen Beispielen der Umriss in der Version mit der dreiteiligen Drehsymmetrie derselbe ist. Tatsächlich ist ein Dreieck nicht durch die Startfigur definiert, sondern durch den Prozess des Skalierens und die Anordnung der in unserem Beispiel jeweils drei skalierten Kopien.

Trotzdem noch einige Versionen mit anderen Startfiguren.

3.4 Mit Quadraten

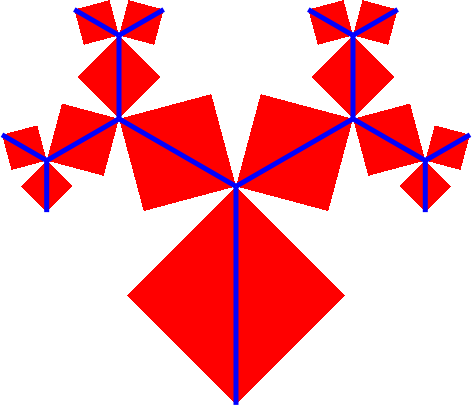
Abb. 8: Mit Quadraten

3.5 Mit regelmäßigen Sechsecken

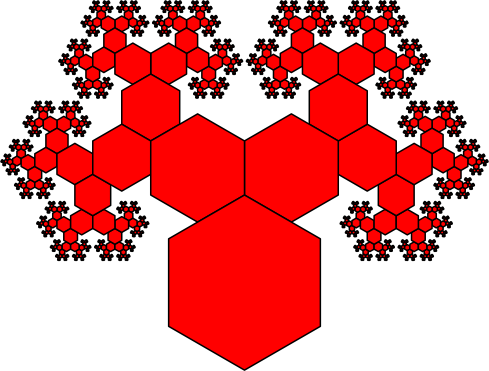
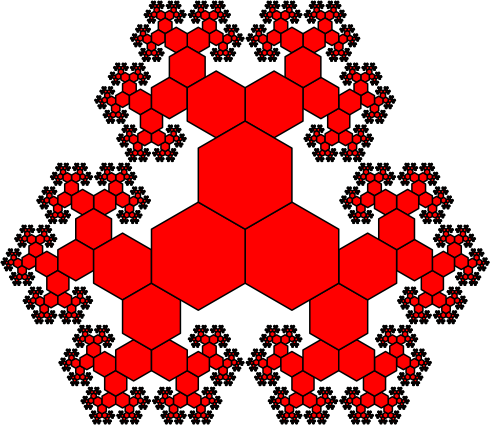
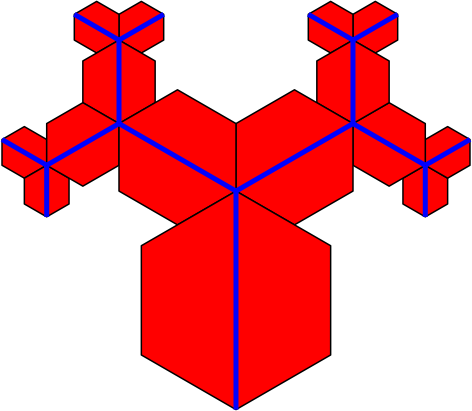
Abb. 9: Regelmäßige Sechsecke

3.6 Mit Kreisen

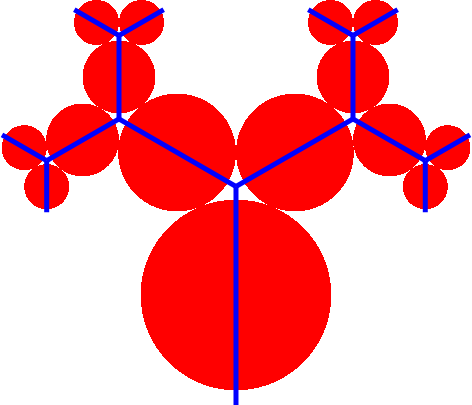
Abb. 10: Kreise

Das Spannende an diesem Beispiel ist natürlich die Frage nach dem Kreisradius und der Position des Kreismittelpunktes. Der Autor hat die vorliegende Studie ausschließlich wegen dieser Frage unternommen.

Die Idee ist natürlich, dass aufeinanderfolgende und nebeneinanderliegende Kreis sich berühren, also weder sich überschneiden noch einen Zwischenraum offenlassen.

Wir setzen die Länge des Stammes auf 1. Weiter sei a der Abstand des Kreismittelpunktes in der Startfigur von der Stammwurzel und r der Radius des Kreises in der Startfigur (Abb. 11).

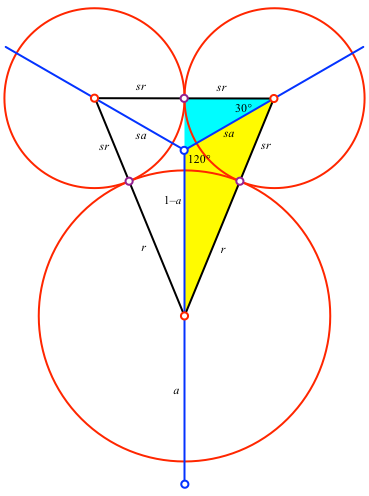
Abb. 11: Bezeichnungen und Daten

Wegen dem Skalierungsfaktor s (kleiner Goldener Schnitt)

haben die beiden kleinen Nachfolgekreise je den Radius sr. Deren Mittelpunkte haben vom Verzweigungspunkt den Abstand sa. Auf Grund des 30°-Winkels im hellblauen Dreieck erhalten wir die Bedingung:

Der Kosinus-Satz im gelben Dreieck liefert:

Damit habe wir zwei Bedingungen für die gesuchten Längen a und r. Es ergibt sich:

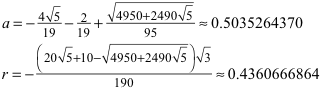
Wir sehen, dass sich die Mittelpunkte der Kreise nicht exakt in der Mitte der blauen Strecken befinden.

Abb. 12: Kreisbaum

Literatur

Walser, H. (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.