Hans Walser, [20220213]

Goldener Baum

1 Worum geht es?

Räumliche Version des ebenen Goldenen Baumes.

2 Baumfraktal

Bei einem Baumfraktal bleibt die Startfigur durchwegs in Originalgröße erhalten.

3 Streckenfraktal

Wir beginnen mit einer senkrechten Strecke (Stamm), und setzen schrittweise verkürzte Verästelungen an (Abb. 1 und 2). Bei einer Verästelung setzen wir vier gleiche Winkel. Die vier Winkel ergeben sich, wenn wir vom Mittelpunkt eines regelmäßigen Tetraeders aus zu den vier Ecken fahren. Dieser Winkel ist:

Es handelt sich hier um einen in der Kristallografie häufig vorkommenden Winkel. Es ist auch der Schnittwinkel der Seitenflächen im regelmäßigen Oktaeder. Ebenso ist es der stumpfe Schnittwinkel zweier Würfeldiagonalen. Ebenso ist es der stumpfe Schnittwinkel der beiden Diagonalen in einem Rechteck im DIN-Format. Über Verallgemeinerungen dieses Winkels siehe hier.

Der Verkleinerungsfaktor s ist so gewählt, dass sich die Äste im Grenzfall weder überschneiden noch eine Lücke offenlassen. Dies führt mit Trigonometrie und Grenzwertüberlegungen (geometrische Reihe) zum Verkleinerungsfaktor s:

Es handelt sich hier um den „kleinen“ Goldenen Schnitt (Walser 2013).

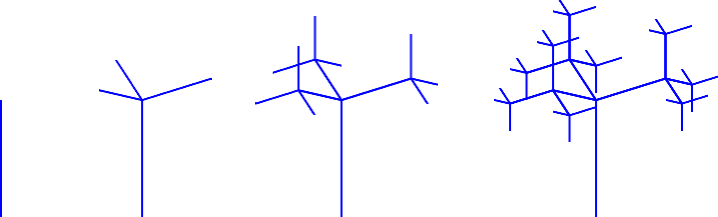
Abb. 1: Entstehung des Baumes

In der Abbildung 2 ist auch die jeweilige Astdicke verkleinert.

Abb. 2: Verkleinerte Astdicken

Abb. 3: Wachsen und Abnehmen

Die Abbildung 4 zeigt die Situation von vorne und in der Drohnensicht.

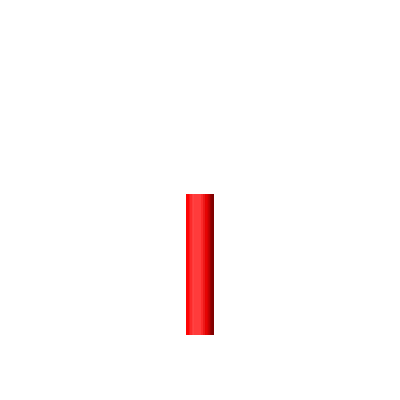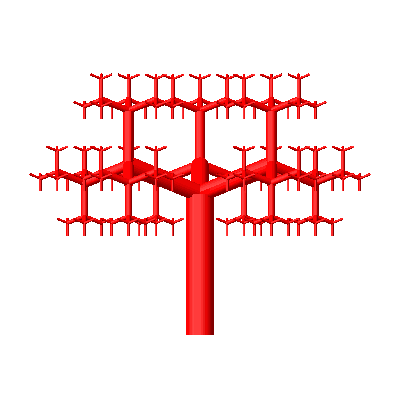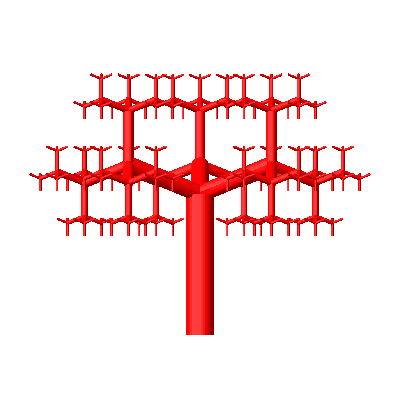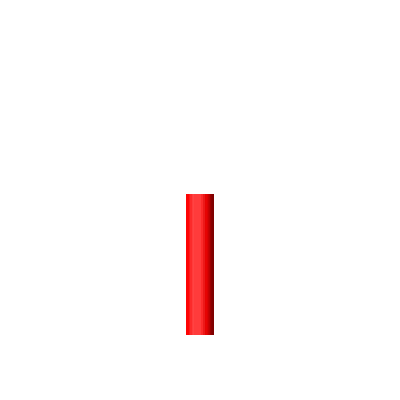
Abb. 4: Spezielle Sichten

Abb. 5: Drehen

4 Vier Bäume

Wir setzen vier Bäume an den Wurzeln so zusammen, dass dort die gleichen Winkel entstehen wie an den Verzweigungspunkten (Abb. 6). Die Gesamtfigur hat dann eine Tetraeder-Symmetrie.

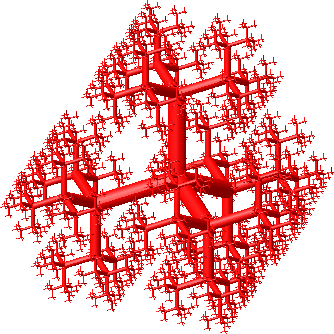
Abb. 6: Vier Bäume

5 Andere Startfiguren

Die Startfigur (in unserem Fall eine Strecke oder ein Zylinder) kann durch andere Figuren ersetzt werden.

5.1 Tetraeder

Nachdem die Winkel an den Verzweigungspunkten dem Tetraeder entnommen sind, ist es naheliegend, an den Verzeigungspunkten wieder Tetraeder einzupassen (Abb. 7 und 8). Die Verzweigungspunkte liegen in den Mittelpunkten der Tetraeder.

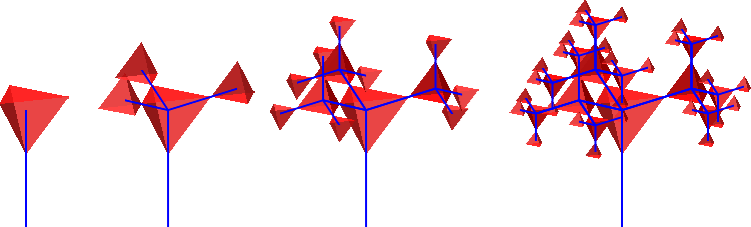
Abb. 7: Transparente Tetraeder

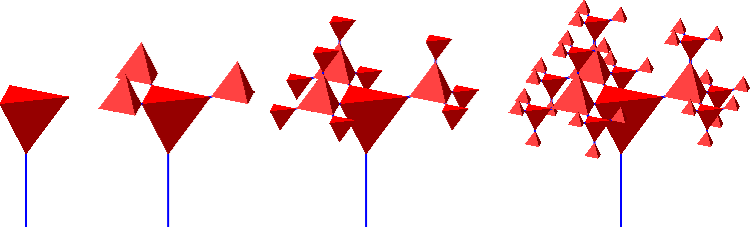
Abb. 8: Intransparente Tetraeder

Abb. 9: Tetraeder an Tetraeder

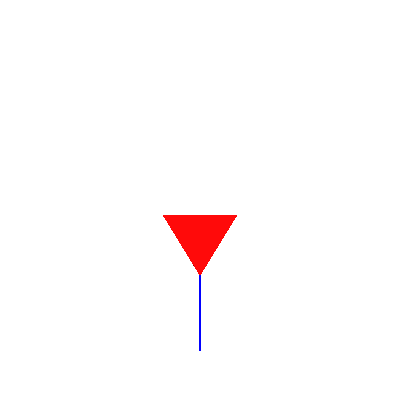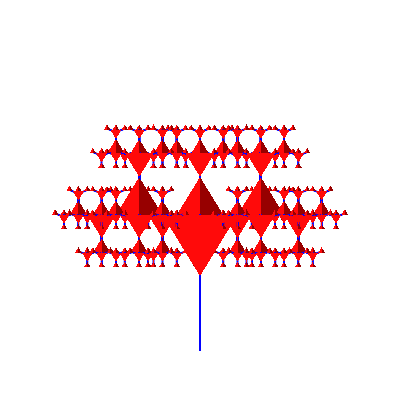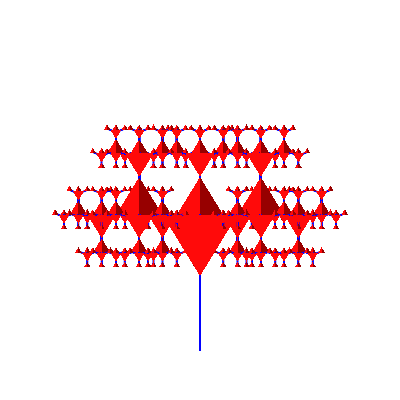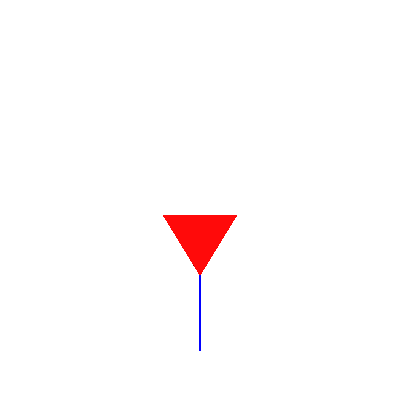
Abb. 10: Spezielle Sichten

Werden vier Tetraeder-Bäume zusammengefügt, bleibt in der Mitte eine Lücke, in welche genau ein weiteres Tetraeder eingefügt werden kann. Das blaue Gerüst kann dann weggelassen werden. Dann verschwinden auch die Blautöne am Rand, welche deshalb entstehen, weil die Tetraeder am Rand kleiner werden als die Gerüstdicke.

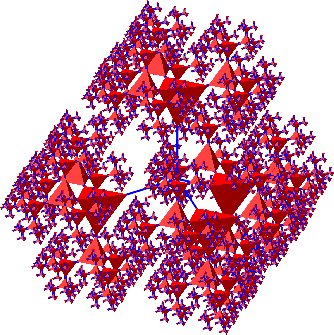
Abb. 11: Vier Tetraeder-Bäume

Abb. 12: Tetraeder-Fraktal

5.2 Kugeln

Auf der Startfigur, also dem Stamm des Baumes, wählen wir einen Punkt und zeichnen eine Kugel darum. Die Kugeln sollen so positioniert und so groß sein, dass sich aufeinanderfolgende Kugeln sowie benachbarte Kugeln derselben Generation berühren (Abb. 13).

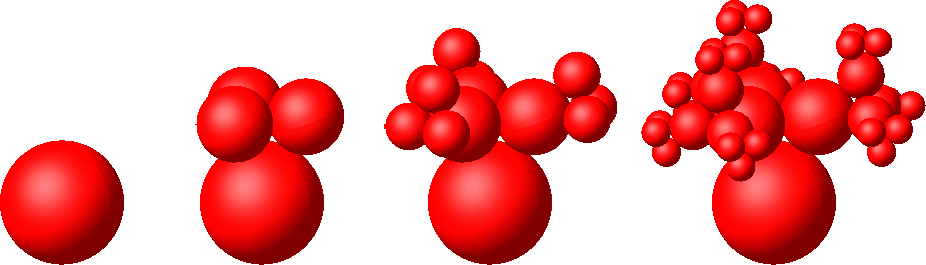
Abb. 13: Kugeln

Wir setzten die Länge des Stammes gleich 1. Der Mittelpunkt der Kugel in der Startfigur habe vom Boden den Abstand a. Der Radius der Kugel in der Startfigur sei r. Mit Überlegungen analog zur entsprechenden Figur in der Ebene finden wir die Bedingungen:

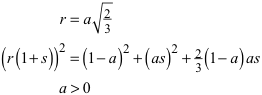
Dieses Gleichungssystem für a und r hat die Lösung:

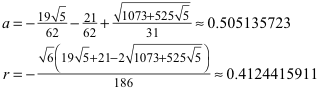
Der Kugelmittelpunkt ist also etwas oberhalb der Mitte des Stammes.

Abb. 14: Kugeln

Natürlich geht es auch mit vier Bäumen in Tetraeder-Symmetrie (Abb. 15).

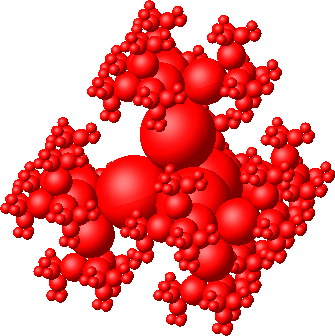
Abb. 15: Noch mehr Kugeln

Websites

Hans Walser: Goldener Baum

http://www.walser-h-m.ch/hans/Miniaturen/G/Goldener_Baum/Goldener_Baum.html

Hans Walser: Simplex

http://www.walser-h-m.ch/hans/Miniaturen/S/Simplex/Simplex.htm

Literatur

Walser, H. (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.