Hans Walser, [20090703b]

Eine Konstruktion des Goldenen Schnittes

Idee von J. N., S.

1        Worum es geht

Es wird eine Konstruktion des Goldenen Schnittes mit einem freien Parameter besprochen.

2        Konstruktionsbeschreibung

Konstruktion

Auf der y-Achse wŠhlen wir einen beliebigen Punkt ; p ist also ein freier Parameter fźr die Konstruktion. Fźr eine reelle Konstruktion muss  sein.

Kreis k um M schneiden mit dem Einheitskreis e; Schnittpunkt S. Gerade g durch Ursprung O und S. Kreis K um M durch Einheitspunkt  auf der x-Achse. Schnitt von K mit g gibt T. Die Strecke OT hat die LŠnge  des Goldenen Schnittes.

3        Nachweis

Einheitskreis e:

 

Kreis k:

 

 

Schnittpunkt S:

 

 

 

 

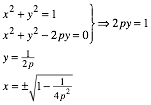
Wir nehmen den positiven Wert und erhalten:

Gerade g:

 

 

Oder in anderer Darstellung:

 

 

Radius R des Kreises K:

 

Kreis K:

 

 

Schnittpunkt T mit der Geraden g:

 

 

 

 

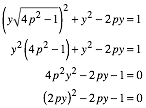
Dies ist die Gleichung des goldenen Schnittes fźr . Es ist also (wir nehmen die positive Lšsung):

 

 

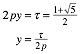
Weiter ist:

 

 

Somit haben wir:

 

 

Fźr den Abstand vom Ursprung ergibt sich:

 

 

Dies war zu beweisen.

4        SonderfŠlle

4.1     

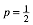
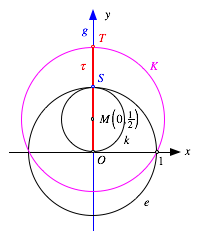
Fźr  fŠllt die Gerade g mit der y-Achse zusammen und wir erhalten eine klassische Konstruktion. Der kleine Kreis k ist nur zur Verdeutlichung eingezeichnet, fźr die Konstruktion ist er nicht erforderlich.

Klassische Konstruktion fźr

4.2     

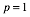
Die Figur lŠsst sich mit einem Quadrat und einem gleichseitigen Dreieck der SeitenlŠngen 1 ergŠnzen.

Konstruktion fźr

Damit kann die Konstruktion einfacher dargestellt werden.

Vereinfachte Darstellung