Hans Walser, [20120708]
Goldener Schnitt mit zwei Dreiecken
Idee: J. N.
1 Die beiden Dreiecke
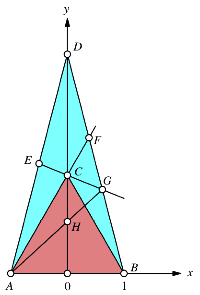
Wir zeichnen ein gleichseitiges Dreieck ABC und ein gleichschenkliges Dreieck ABD, dessen Schenkel doppelt so lang sind wie die Basis AB. E ist der Mittelpunkt des Schenkels AD.
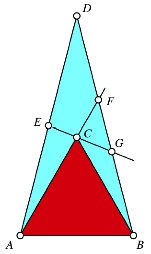
Die beiden Dreiecke
Die Gerade AC schneidet den Schenkel DB im Punkt F, die Gerade EC schneidet diesen Schenkel im Punkt G.
Die beiden Punkte F und G teilen den Schenkel BD je im VerhŠltnis des Goldenen Schnittes.
2 Beweis
Wir verwenden ein Koordinatensystem gemŠ§ Abbildung.
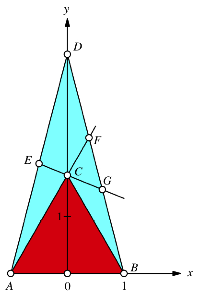
Koordinaten
ZunŠchst ergeben sich die Koordinaten:
![]()
Fźr das VerhŠltnis des Goldenen Schnittes verwenden wir die Schreibweise:
![]()
Mit einiger Rechnung ergeben sich fźr F und G die Koordinaten:
![]()
Fźr den
Nachweis des Goldnen Schnittes genźgen die x-Koordinaten
der Punkte D, F, G, B. Diese sind ![]() . Dies war zu beweisen.
. Dies war zu beweisen.
3 Konstruktionen
Damit ergeben sich die in der Abbildung angedeuteten beiden Konstruktionswege fźr den Goldenen Schnitt.
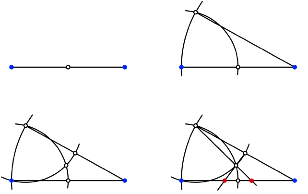
Konstruktionen
4 Pentagramm
Die TeilverhŠltnisse auf dem Schenkel BD sind dieselben wie beim Pentagramm.
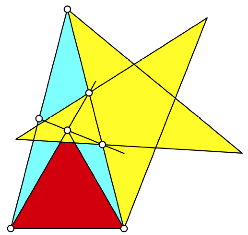
Pentagramm
5 ErgŠnzungen
Wir erhalten weiter folgende VerhŠltnisse:
![]()
Die Gerade AG schneide die y-Achse im Punkt H. Der Punkt H teilt die Strecke AG im VerhŠltnis des Goldenen Schnittes:
![]()
Noch ein Punkt