Hans Walser, [20091223a]

Goldener Schnitt mit drei Kreisen und Dreiecken

Idee und Anregung: J. N.  (vgl. [Prinz 2009], S. 20, Abb. 19)

1        Konstruktion mit drei Kreisen

Die folgende Konstruktion wurde von K. Hofstetter gefunden [Hofstetter 2002]. Wir beginnen mit zwei Kreisen gemŠ§ Figur. Der Mittelpunkt des einen Kreises ist jeweils auf der Kreislinie des anderen.

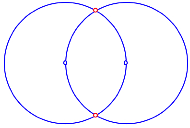
Zwei Kreise

Nun setzen wir einen dritten, gleich gro§en Kreis berźhrend auf.

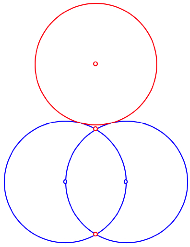
Dritter Kreis

In dieser Situation liegen der Mittelpunkt dieses dritten Kreises und die beiden Schnittpunkte der ersten beiden Kreise im VerhŠltnis des goldenen Schnittes.

Beweis: Der Radius der Kreise sei 1. Der lŠngere Abschnitt, zwischen den beiden Schnittpunkten der ersten beiden Kreise, hat die LŠnge . Fźr den kźrzeren Abschnitt erhalten wir:

 

Damit ergibt sich das LŠngenverhŠltnis des goldenen Schnittes:

 

2        Variante mit Dreiecken

Auf derselben Basis bauen wir ein gleichschenkliges Dreieck, dessen Schenkel doppelt so lang sind wie die Basis, ein gleichseitiges Dreieck mit Spitze nach oben und ein gleichseitiges Dreieck mit Spitze nach unten.

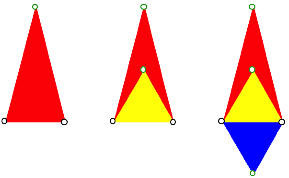
Dreiecke

Die drei Spitzen liegen dann im VerhŠltnis des goldenen Schnittes. Beweis analog.

Literatur

[Hofstetter 2002]        Hofstetter, Kurt: A Simple Construction of the Golden Section. Forum Geometricorum, 2 (2002), p. 65-66.

[Prinz 2009]               Prinz, Ina: Jo Niemeyer im Arithmeum. Berlin: Nicolai 2009. ISBN 978-3-89479-904-4