Hans Walser, [20230736]

Goldener Schnitt

1 Worum es geht

Kinematische Spielerei, welche zum Goldenen Schnitt führt.

2 Kinematik

Die Abbildung 1 zeigt fünf ähnliche rechtwinklige Dreiecke. Vier davon (grün, gelb, magenta, orange) sind sogar kongruent. Das fünfte Dreieck (hellblau) ist in der Regel kleiner oder größer.

Abb. 1: Kinematik

3 Forschungsfrage

Wann genau ist auch das hellblaue Dreieck gleich groß, also zu den anderen kongruent? (Zwischenstopp in Abb. 1, Abb. 2).

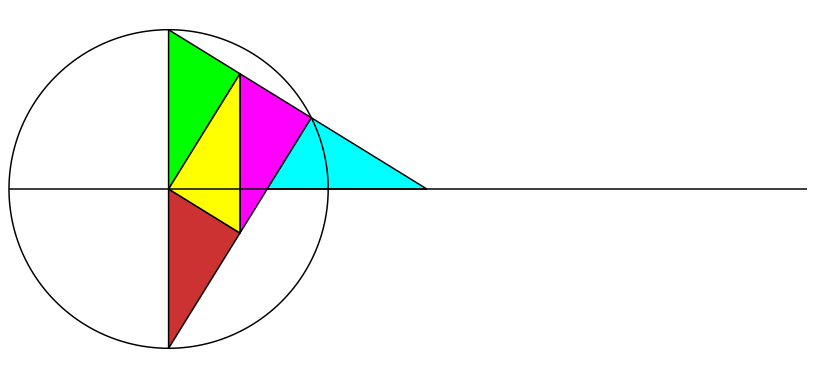
Abb. 2: Fünf kongruente Dreiecke

4 Kreisspiegelung

Zunächst eine Vorbereitung. Wir passen den Umriss der allgemeinen Figur in ein Koordinatensystem ein (Abb. 3). Der Kreis ist der Einheitskreis. Die beiden relevanten Punkte auf der x-Achse haben die x-Koordinaten p und q.

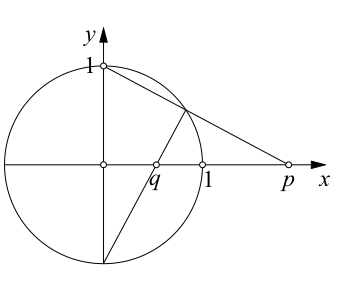
Abb. 3: Koordinatensystem

Nun färben wir neue rechtwinklige Dreiecke ein (grau und lila in Abb. 4). Das graue Dreieck hat die lange Kathete p und das lila Dreieck die kurze Kathete q.

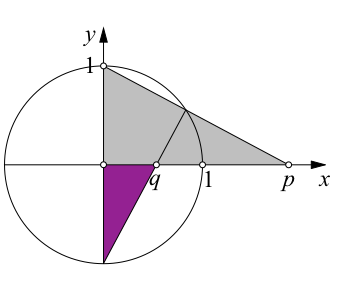
Abb. 4: Graues und lila Dreieck

Wir spiegeln das lila Dreieck am Kreismittelpunkt (Abb. 5).

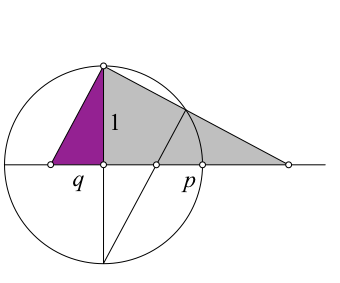
Abb. 5: Spiegelung am Kreismittelpunkt

Die beiden Dreiecke bilden nun zusammen ein großes rechtwinkliges Dreieck. Es hat die Hypotenusenabschnitte p und q und die Höhe 1.

Nach dem Höhensatz ist pq = 1. Somit sind p und q Kehrwerte voneinander, also q = 1/p.

Dieses Prozedere wird manchmal als Spiegelung am Einheitskreis bezeichnet.

5 Goldener Schnitt

Die vier ohnehin schon kongruenten Dreiecke haben die Hypotenusenlänge 1. Dies muss für unser Problem nun auch für das hellblaue Dreieck gelten, also:

p – q = 1

Wegen q = 1/p ergibt sich:

p – 1/p = 1

Wir erhalten daraus die quadratische Gleichung:

p² – p – 1 = 0

Die für uns relevante Lösung ist p = Φ, also der Goldene Schnitt. In die Lösungsfigur (Abb. 6) können wir passend Major und Minor einzeichnen.

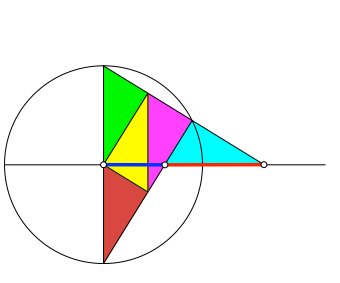
Abb. 6: Goldener Schnitt

Weblink

Hans Walser: Goldener Schnitt

http://www.walser-h-m.ch/hans/Miniaturen_Uebersicht/Goldener_Schnitt/index.html