1 Worum es geht

Der Goldene Schnitt erscheint in einem nicht ganz regelmäßigen Oktaeder.

2 Das Oktaeder

Wir setzen acht rechtwinklig-gleichschenklige Dreiecke zu einem Oktaeder zusammen (Abb. 1 und 2).

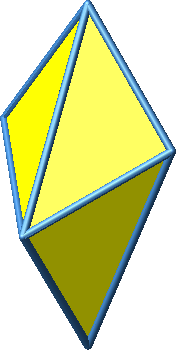
Abb. 1: Oktaeder

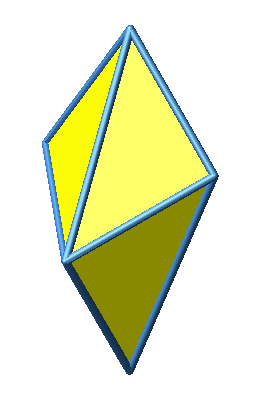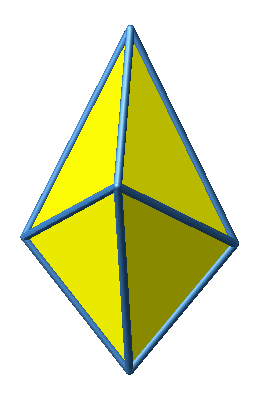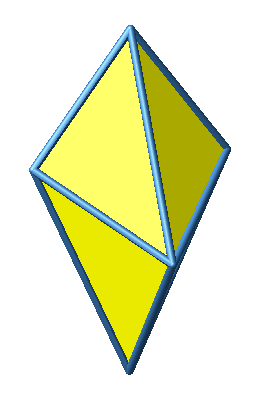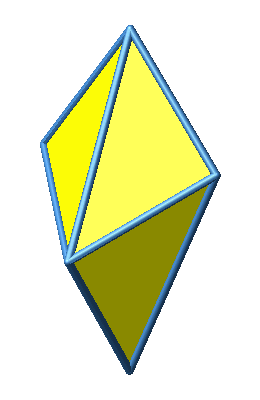
Abb. 2: Verschiedene Sichten

Dieses Oktaeder hat acht kurze und vier lange Kanten. Eine lange Kante ist √2-mal so lang wie eine kurze Kante. Die kurzen Kanten sind Katheten der rechtwinklig-gleichschenkligen Dreiecke, die langen Kanten Hypotenusen.

Ein solches Oktaeder kann aus acht Geo-Dreiecken zusammengebaut werden.

3 Diagonalen

Nun zeichnen wir die drei Diagonalen ein (Abb. 3 und 4).

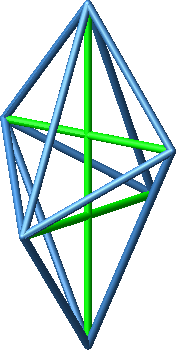
Abb. 3: Diagonalen

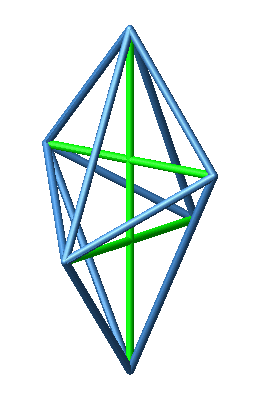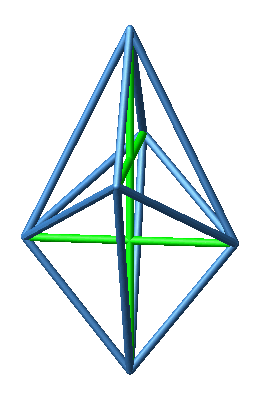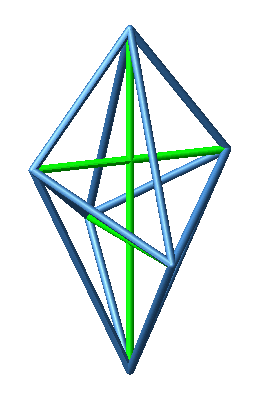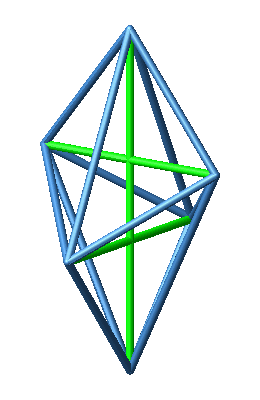
Abb. 4: Diagonalen

4 Goldener Schnitt

Die beiden kurzen Diagonalen unterteilen die lange Diagonale im Verhältnis des Goldenen Schnittes, und zwar in der Reihenfolge Major (rot), Minor (blau), Major (rot) (Abb. 5). Nachweis durch Rechnung.

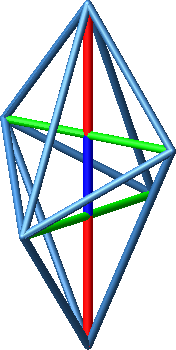
Abb. 5: Goldener Schnitt

Eine kurze Oktaederkante und eine halbe kurze Diagonale stehen ebenfalls im Verhältnis des Goldenen Schnittes (Abb. 6).

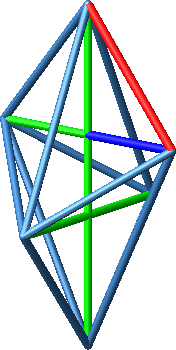
Abb. 6: Goldener Schnitt

Weblink

Hans Walser: Goldener Schnitt

https://walser-h-m.ch/hans/Miniaturen_Uebersicht/Goldener_Schnitt/index.html