1 Worum es geht

In einem speziellen Dreieck im Quadratgitter erscheint der Goldene Schnitt.

2 Das Dreieck

Die Abbildung 1 zeigt das Dreieck im Quadratgitter.

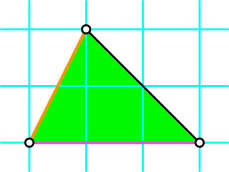
Abb. 1: Dreieck im Quadratgitter

3 Verlängern der Seiten

Wir verlängern zwei der drei Seiten gemäß Abbildung 2.

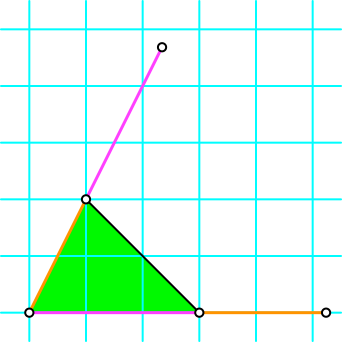
Abb. 2: Seiten Verlängern

Nun können wir ein Rechteck mit dem Seitenverhältnis des Goldenen Schnittes einpassen (Abb. 3). Die Seiten des Goldenen Rechteckes sind mit Major (rot) und Minor (blau) markiert.

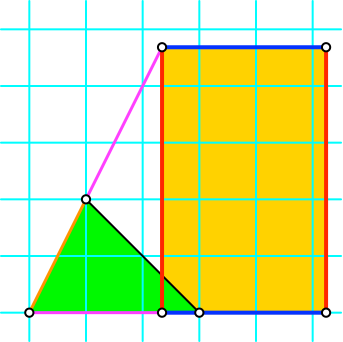
Abb. 3: Goldenes Rechteck

Nachweis rechnerisch.

4 Punkspiegelung

Wir spiegeln die Figur an derjenigen Ecke, von welcher keine Seitenverlängerung ausgeht (Abb. 4).

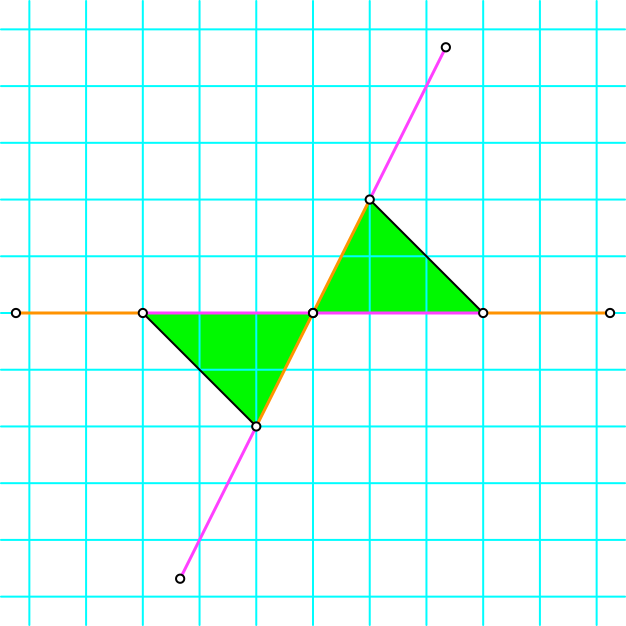
Abb. 4: Punktspiegelung

Die konvexe Hülle der Figur ist ein Goldenes Rechteck (Abb. 5).

Abb. 5: Goldenes Rechteck als konvexe Hülle

5 Inkreise

Statt die Seiten zu verlängern, zeichnen wir die Inkreise (Abb. 6).

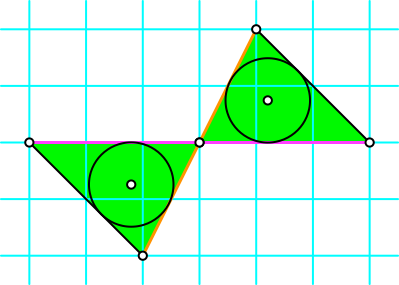
Abb. 6: Inkreise

Ein Goldenes Rechteck wird durch Berührungspunkte definiert (Abb. 7).

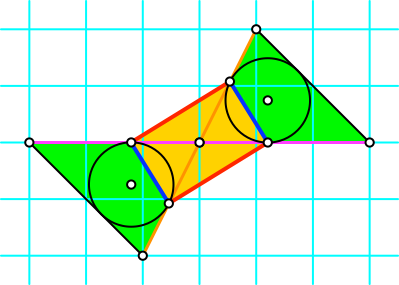
Abb. 7: Berührungspunkte definieren ein Goldenes Rechteck

6 Zweites Quadratgitter

Wir bauen ein zweites Quadratgitter ein, welches an der orangen Dreiecksseite orientiert ist (Abb. 8).

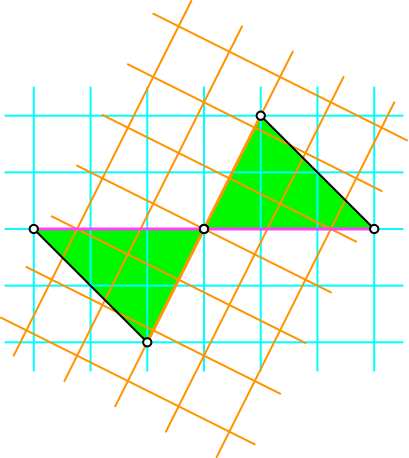
Abb. 8: Zweites Quadratgitter

Eine geeignete Auswahl von Gitterpunkten der beiden Quadratgitter ergibt ein Goldenes Rechteck (Abb. 9).

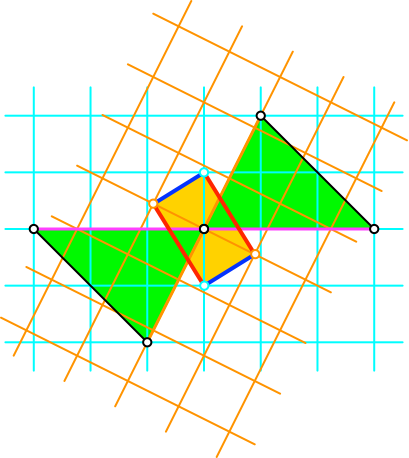
Abb. 9: Goldenes Rechteck

Es gibt viele weitere Lösungen dieser Art.

7 Hintergrund

Die Winkel im Dreieck (Abb. 10) sind sehr speziell.

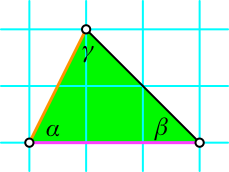
Abb. 10: Dreieckswinkel

Der Winkel α = arctan(2) ≈ 63.434948822922011° ist der Diagonalenschnittwinkel im Goldenen Rechteck.

Der Winkel β = arctan(1) = 45° ist der Diagonalenschnittwinkel im Zentrum des regelmäßigen Achteckes.

Für den Winkel γ = arctan(3) ≈ 71.565051177077989° habe ich keine schöne geometrische Bedeutung gefunden.

Es gilt die schöne Formel:

arctan(1) + arctan(2) + arctan(3) = 180°

Diese Formel kann unmittelbar im Quadratgitter eingesehen werden (Abb. 11).

Abb. 11: Beweisfigur

Weblinks

Hans Walser: Miniaturen: Goldener Schnitt

https://walser-h-m.ch/hans/Miniaturen_Uebersicht/Goldener_Schnitt/index.html