Hans Walser, [20240216]
Goldener Schnitt
Idee und Anregung: Jo Niemeyer, Berlin
1 Worum es geht
Die Fibonacci-Rekursion wird auf Volumina von Würfeln angewendet.
2 Problemstellung
Die Abbildung 1 zeigt drei Würfel. Das Volumen des roten Würfels ist gleich der Summe der Volumina des gelben und des blauen Würfels.
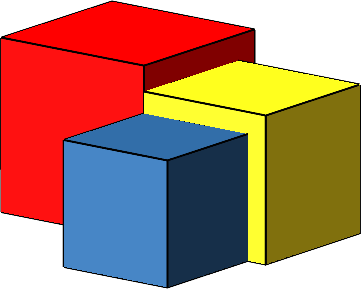
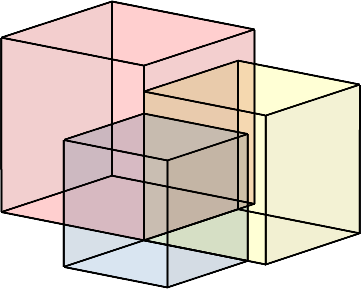
Abb. 1: Drei Würfel
Die Verkleinerung der Kantenlänge des roten Würfels zur Kantenlänge des gelben Würfels ist prozentual gleich groß wie die Verkleinerung der Kantenlänge des gelben Würfels zur Kantenlänge des blauen Würfels. Wie groß ist dieser Prozentsatz?
3 Bearbeitung
Mit f bezeichnen wir den Faktor für die Verkleinerung der Würfelkanten. Für die Würfelkanten haben wir also das Verhältnis 1 : f : f2.
Die Volumenbedingung liefert:
1 = f3 + (f2)3
1 = f3 + (f3)2
Daraus ergibt sich f3 = 1/Φ. Dabei ist Φ = (1 + √5)/2 ≈ 1.618 der Goldene Schnitt.
Für f erhalten wir:
f = (1/Φ)^(1/3) ≈ 0.8518 ≈ 1 – 0.1482.
Die Abnahme beträgt also etwa 14.82%.
4 Iteration
Wir können im gleichen Verhältnis weiter verkleinern (Abb. 2). Das Volumen des gelben Würfels ist gleich der Summe der Volumina des blauen und des kleinen roten Würfels.
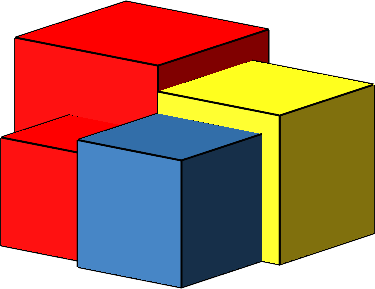
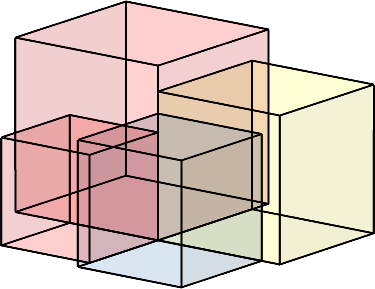
Abb. 2: Ein vierter Würfel
Hier erscheint der Goldene Schnitt auch als Längenverhältnis. Die Kantenlängen des großen und des kleinen roten Würfels sind im Verhältnis des Goldenen Schnittes (in der Abbildung 3 durch Major (rot) und Minor (blau) dargestellt).
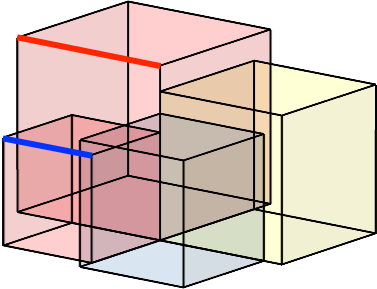
Abb. 3: Major und Minor
Bei Weiterführung entsteht eine eckige logarithmische Spirale.
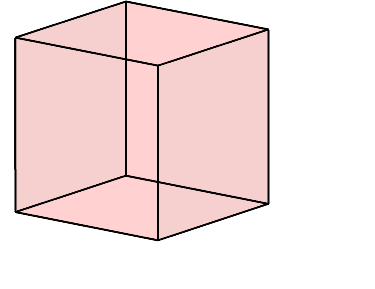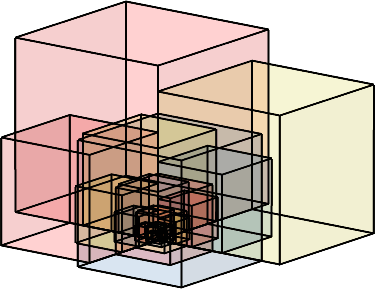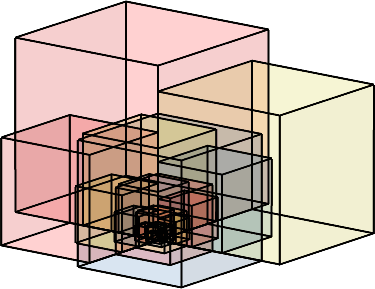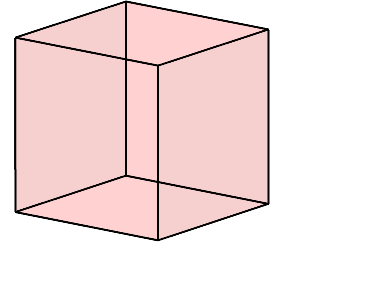
Abb. 4: Würfelfolge
Die Abbildungen 5 und 6 zeigen die Würfelfolge in einer Sicht von oben beziehungsweise von vorne.

Abb. 5: Sicht von oben
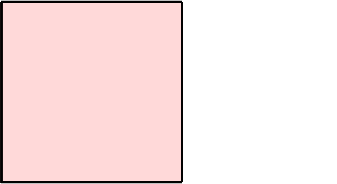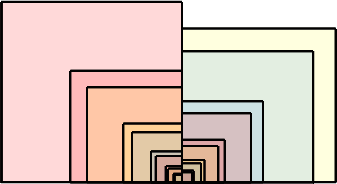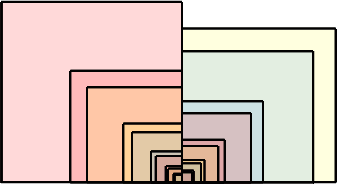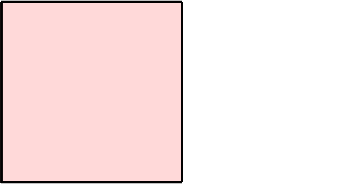
Abb. 6: Sicht von vorne
5 Turmbau
In der Abbildung 7 sind die ersten drei Würfel mittig und kantenparallel aufeinandergestellt.
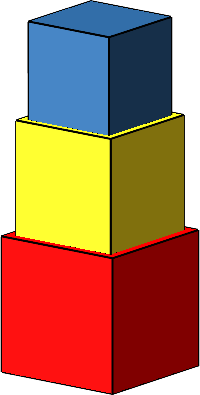
Abb. 7: Turm
6 Turmbau zu Babel
Durch Iteration erhalten wir einen Turm aus unendlich vielen Würfeln (Abb. 8).

Abb. 8: Turmbau zu Babel
7 Endliche Höhe und Volumen
Obwohl wir unendlich viele Würfel aufeinanderstapeln, bleibt die Gesamthöhe des Turmes endlich. Bei einer Kantenlänge 1 des untersten Würfels ergibt sich für die Gesamthöhe der Grenzwert:
Gesamthöhe = Φ^(1/3)/( Φ^(1/3) – 1) ≈ 6.7476
Auch das Gesamtvolumen ist endlich und ergibt eine schöne Formel:
Gesamtvolumen = Φ2 ≈ 2.618
Dass das Bauprojekt des Turms zu Babel trotzdem scheiterte, lag an den Finanzen. Diese wuchsen ins Uferlose.
8 Spiralenturm
Wir stapeln die Würfel verdreht aufeinander (Abb. 9). Dabei wird jeder Würfel so weit gedreht, dass er den unteren nicht überkragt.
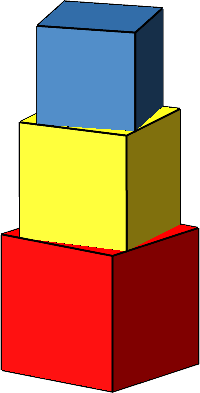
Abb. 9: Verdrehter Würfelstapel
Der benötigte Drehwinkel ist:
Drehwinkel = arcsin(Φ^(1/3) •√2/2) – π/4 ≈ 0.1939 ≈ 11.1124°
Die Abbildung 10 zeigt den Aufbau des Spiralenturms.

Abb. 10: Aufbau des Spiralenturms
9 Anordnung in der Ebene
Die Abbildung 11 zeigt eine weitere Anordnung der ersten drei Würfel.

Abb. 11: Anordnung in der Ebene
Der vierte Würfel kann jetzt so angesetzt werden, dass er den roten Würfel nicht berührt (Abb. 12). Die Kantenlängen des großen und des kleinen roten Würfels stehen im Verhältnis des Goldenen Schnittes.

Abb. 12: Vierter Würfel
Die Abbildung 13 zeigt die weitere Expansion.

Abb. 13: Expansion
Weblink
Hans Walser: Miniaturen: Goldener Schnitt
https://walser-h-m.ch/hans/Miniaturen_Uebersicht/Goldener_Schnitt/index.html
Literatur
Walser, Hans (2022): Spiralen, Schraubenlinien und spiralartige Figuren. Mathematische Spielereien in zwei und drei Dimensionen. Springer Spektrum. ISBN 978-3-662-65131-5 und ISBN 978-3-662-65132-2 (eBook).