Hans Walser, [20240917a]

Goldener Schnitt

Idee und Anregung: Wilfried Dutkowski, Bonn

1 Problemstellung

Einem Quadrat ist ein kleineres Quadrat (gelb in Abb. 1) einzubeschreiben.

Abb. 1: Problemstellung

Die Abbildung 2 zeigt das kinematische Einpassen.

Abb. 2: Kinematisches Einpassen

2 Lösung

Der Goldene Schnitt, in der Abbildung 3 angegeben durch Major und Minor, führt zur Lösung.

Abb. 3: Lösung mit dem Goldenen Schnitt

3 Beweis

Im Einheitsquadrat gehen wir von einem allgemeinen Fall aus (Abb. 4).

Abb. 4: Allgemeiner Fall

Das grüne und das magenta Dreieck sind ähnlich und haben das Längenverhältnis 1 : h.

Abb. 5: Ähnliche Dreiecke

Die in der Abbildung 6 eingezeichneten Höhen haben daher auch das Längenverhältnis 1 : h. Da ihre Summe 1 ist, ergeben sich für die beiden Höhen die eingezeichneten Längen.

Abb. 6: Höhen

Die beiden kongruenten rechtwinkligen Dreiecke (hellblau in Abb. 7) haben die lange Kathete h/(1 + h).

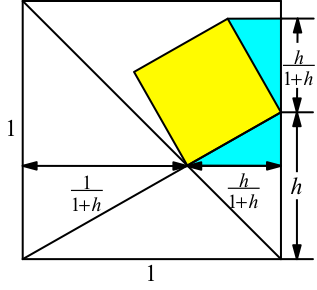
Abb. 7: Kongruente rechtwinklige Dreiecke

Der oberste Eckpunkt des gelben Quadrates hat also von der Basislinie des Einheitsquadrates den Abstand h + h/(1 + h).

Die Bedingung, dass der oberste Eckpunkt des gelben Quadrates auf der Decklinie des Einheitsquadrates liegt, führt auf die Gleichung:

h + h/(1 + h) = 1

Daraus erhalten wir die quadratische Gleichung:

h² + h = 1

Die positive Lösung ist h = 1/ Φ ≈ 0.618. Dabei ist Φ = (1 + √5)/2 ≈ 1.618 der Goldene Schnitt. Daraus folgt die Behauptung der Abbildung 3.

4 Bahnkurven

Die Bahnkurve des obersten Eckpunktes des gelben Quadrates ist die Hyperbel (Abb. 8) mit der Gleichung:

(x – 3)² – y² = 4

Dabei wird das Koordinatensystem so definiert, dass der Ursprung in die linke untere Ecke des Einheitsquadrates zu liegen kommt.

Die Bahnkurve des zweitobersten Eckpunktes des gelben Quadrates ist die Hyperbel mit der Gleichung:

xy – 2x – 2y = –2

Abb. 8: Bahnkurven

5 Variante

Die Abbildungen 9 und 10 zeigen eine Variante.

Abb.9: Variante

Abb. 10: Kinematik der Variante

Die Lösung ergibt sich wiederum mit dem Goldenen Schnitt (Abb. 11).

Abb. 11: Lösung mit dem Goldenen Schnitt

Die Bahnkurven sind Geraden mit den Steigungen 1 und 0 (Abb. 12).

Abb. 12: Bahnkurven

Weblinks

Hans Walser: Miniaturen: Goldener Schnitt

https://walser-h-m.ch/hans/Miniaturen_Uebersicht/Goldener_Schnitt/index.html

Literatur

Walser, Hans (2024): Der Goldene Schnitt. Geometrische und zahlentheoretische Betrachtungen. 7. Auflage. Springer Spektrum.
Print-ISBN 978-3-662-68556-3. E-Book_ISBN 978-3-662-68557-0.
https://doi.org/10.1007/978-3-662-68557-0