Hans Walser, [20111011a]

Konstruktion des Goldenen Schnittes mit einem Parameter

Mathematische Ausarbeitung einer Idee von J. N., S.

1 Idee von J. N.

Die Abbildung 1 von J. N. beschreibt die Konstruktion auf der Basis eines rechteckigen Papierblattes.

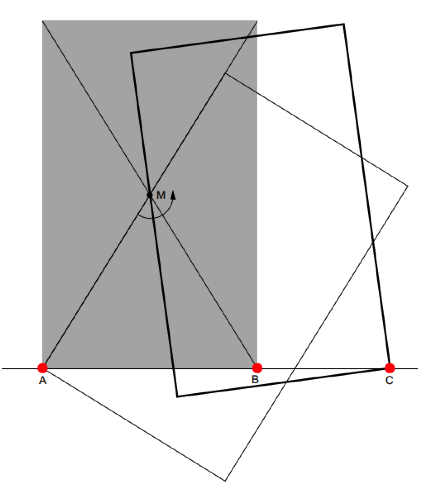
Abb. 1: Konstruktion (Zeichnung von J. N.)

Ein Rechteck wird um die linke untere Ecke A gedreht, bis die linke Kante auf den Mittelpunkt M zu liegen kommt. Dann wird um diesen Mittelpunkt M gedreht, bis die Ecke rechts unten auf die Standlinie zu liegen kommt. Die in der Abbildung angegebene Strecke steht dann im Verhältnis des Goldenen Schnittes zur Rechteckskante .

2 Beweis

Für den mathematischen Beweis reduzieren wir die geometrische Konstruktion auf das Minimum. Wir verwenden die Bezeichnungen der Abbildung 2.

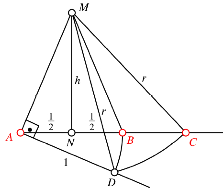
Abb. 2: Beweisfigur

Wir beginnen mit dem gleichschenkligen Dreieck ABM. Die Basislänge normieren wir auf 1, die Höhe h ist der freie Parameter. Diese Höhe h ist die halbe Höhe des ursprünglichen Rechtecks.

In A zeichnen wir die Normale zum Dreiecksschenkel AM und schneiden diese mit dem Kreis um A durch B. Der Schnittpunkt sei D.

Den Kreis um M durch D schneiden wir mit der Geraden AB, der Schnittpunkt sei C.

Die Strecke steht dann im Verhältnis des Goldenen Schnittes zur Basis .

Beweis:

Für die Schenkellänge erhalten wir nach Pythagoras:

Daraus erhalten wir für den Radius r:

Für die Strecke ergibt sich:

Somit ist :

Dies ist der Goldene Schnitt.

Die Abbildung 3 zeigt den Konstruktikonsvorgang mit Rechtecken in drei Bildern. Der freie Parameter ist die (halbe) Höhe des Ausgangsrechteckes.

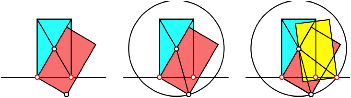
Abb. 3: Konstruktionsvorgang

3 Ein Sonderfall

Wir arbeiten im Dreiecksraster und starten mit dem in der Abbildung 4 eingezeichneten Rechteck.

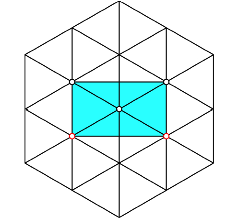
Abb. 4: Rechteck im Dreiecksraster

Die Konstruktion des Goldenen Schnittes führt zur Figur der Abbildung 5.

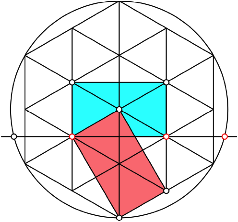
Abb. 5: Konstruktion des Goldenen Schnittes

Das erinnert an die Konstruktion von Odom (vgl. [Walser 2009], S. 83). Tatsächlich ergibt sich die Idee von Odom durch Einzeichnen eines geeigneten Dreiecks (Abb. 6).

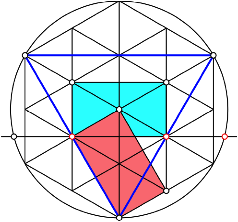
Abb. 6: Idee von Odom

4 Ein Grenzfall

Die Abbildung 7 zeigt die Situation für ein sehr flaches Startrechteck.

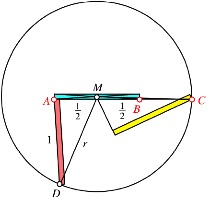
Abb. 7: Flaches Startrechteck

Für erhalten wir daraus eine klassische Konstruktion des Goldenen Schnittes (Abb. 8).

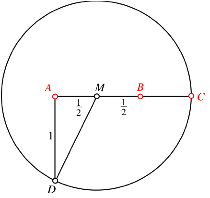
Abb. 8: Klassische Konstruktion des Goldenen Schnittes

5 Variante der Konstruktion

Statt mit dem gleichschenkligen Dreieck können wir auch mit dem rechten Winkel beginnen (Abb. 9). Auf dem einen Schenkel wählen wir D im Abstand 1 vom Scheitel A, auf dem anderen Schenkel in beliebigem Abstand den Punkt M. Nun zeichnen wir einen Kreis um M durch A und einen Kreis um A durch D. Der Schnittpunkt B führt zum gleichschenkligen Dreieck ABM.

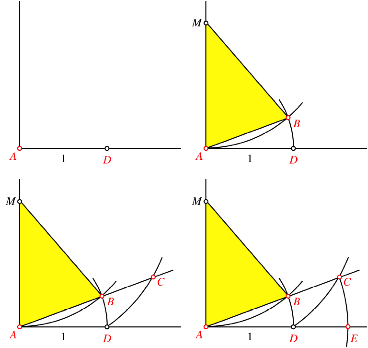
Abb. 9: Variante der Konstruktion

Weiter zeichnen wir um M einen Kreis durch D und erhalten mit der Geraden AB den Schnittpunkt C. Die Strecke steht dann im Verhältnis des Goldenen Schnittes zur Strecke . Wir können dieses Verhältnis mit einem Kreis um A durch C auf den unteren Schenkel des rechten Winkels übertragen.

Literatur

[Walser 2009] Walser, Hans: Der Goldene Schnitt. 5., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Edition am Gutenbergplatz, Leipzig 2009. ISBN 978-3-937219-98-1