Hans Walser, [20221103]
Goldener Schnitt
Idee und Anregung: Maik Rentsch
1 Worum geht es?
Im Kontext eines Theorems von Stanley Rabinowitz erscheint der Goldene Schnitt
2 Das Theorem von Rabinowitz
Wir zeichnen zwei Kreise, die sich von innen berühren (Abb. 1). Auf dem äußeren Kreis wählen wir einen beliebigen Punkt und zeichnen von diesem Punkt einerseits die Sehne zum Berührungspunkt der beiden Kreise und andererseits einen Tangentenabschnitt zum inneren Kreis.
Das Längenverhältnis Sehne / Tangentenabschnitt ist unabhängig von der Wahl des Punktes auf dem äußeren Kreis.
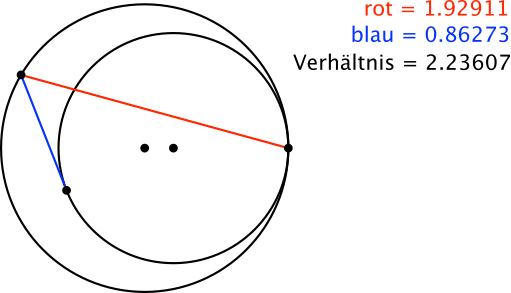
Abb. 1: Theorem von Rabinowitz
Die Abbildung 2 illustriert den Sachverhalt. Die einzelnen Streckenlängen variieren, ihr Verhältnis bleibt invariant.
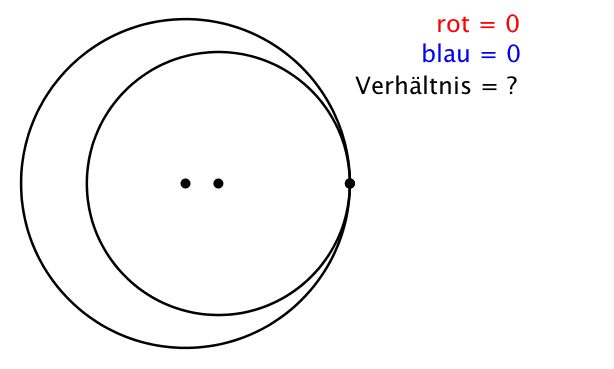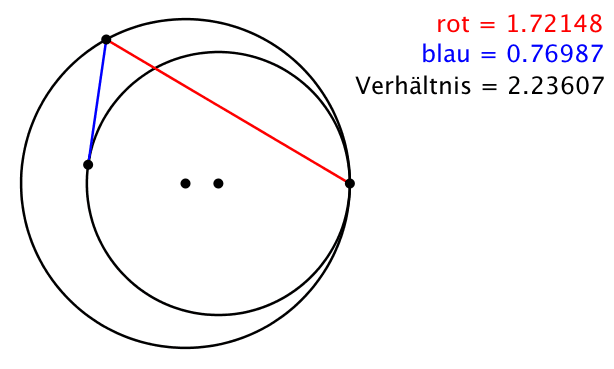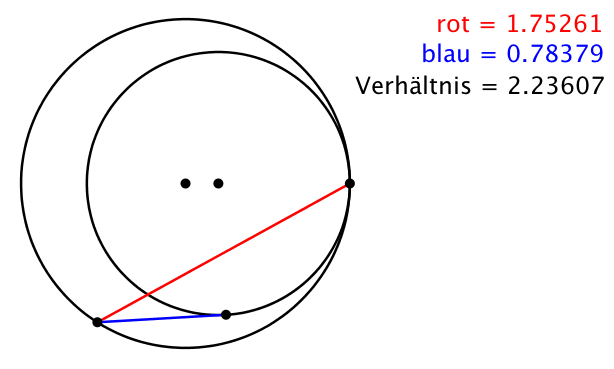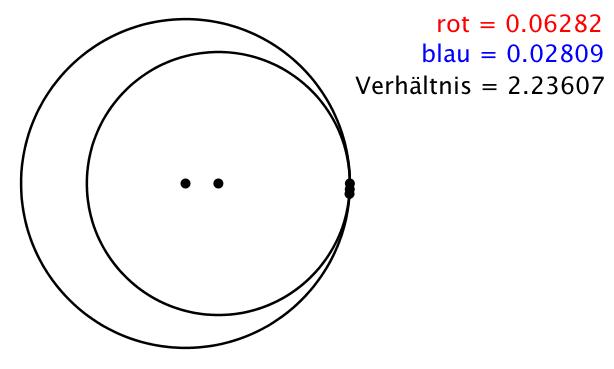
Abb. 2: Animation
3 Beweis
Wir arbeiten mit den Bezeichnungen der Abbildung 3. Der äußere Kreis sei der Einheitskreis mit dem Zentrum A im Ursprung. Der innere Kreis hat den Radius r und das Zentrum C( 1–r, 0). Der Berührungspunkt B der beiden Kreise hat die Koordinaten B(1, 0).
Gesucht ist das Verhältnis c / d.
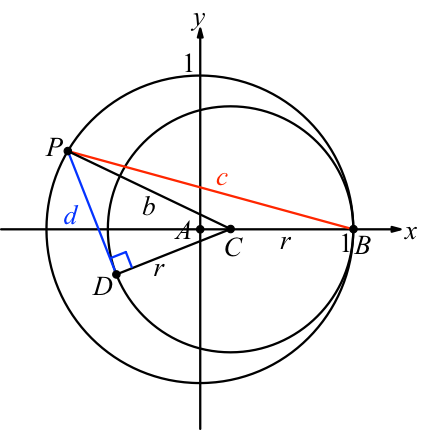
Abb. 3: Maße und Bezeichnungen
Aus Symmetriegründen können wir uns auf die obere Hälfte beschränken. Der Punkt P habe die Koordinaten P(x, √(1–x2)).
Für die Sehnenlänge c erhalten wir:
(1) c2 = (1 – x)2 + (√(1–x2))2 = 1 – 2x + x2 + 1 – x2 = 2 – 2x = 2(1 – x)
Für die Strecke b ergibt sich:
(2) b2 = (1 – r – x)2 + (√(1–x2))2 = 1 + r2 + x2 – 2r – 2x + 2rx + 1 – x2 = 2 + r2 – 2r – 2x + 2rx
Damit erhalten wir für den Tangentenabschnitt d:
(3) d2 = b2 – r2 = 2 + r2 – 2r – 2x + 2rx – r2 = 2 – 2r – 2x + 2rx = 2(1 – x)(1 – r)
Für das gesuchte Verhältnis c / d ergibt sich aus (1) und (3):
(4) c2 / d2 = (2(1 – x)) / (2(1 – x)(1 – r)) = 1 / (1 – r)
(5) c / d = 1 / √(1 – r)
Das Verhältnis ist nur vom Radius r des inneren Kreises abhängig und damit invariant bei Verdrehungen des Punktes P auf dem äußeren Kreis. Dies war zu beweisen.
4 Sonderfall
Wir fragen nun, für welchen Radius r des inneren Kreisen die beiden kleinen rot / blauen Strecken (Abb. 4) im selben Verhältnis stehen wie die großen.
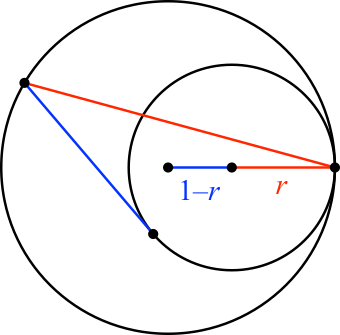
Abb. 4: Zusatzbedingung
Die Bedingung dazu ist:
(6) c / d = r / (1 – r)
Aus (5) erhalten wir:
(7) 1 / √(1 – r) = r / (1 – r)
Dies lässt sich umformen zur quadratischen Gleichung:
(8) r2 + r – 1 = 0
Die positive Lösung ist:
(9) r = (– 1 + √5)/2 ≈ 0.618
Dies ist der Kehrwert des Goldenen Schnittes Φ = (1 + √5)/2 ≈ 1.618.
Für das Verhältnis c / d ergibt sich damit der Goldene Schnitt (Abb. 5):
(10) c / d = (1 + √5)/2 = Φ ≈ 1.618
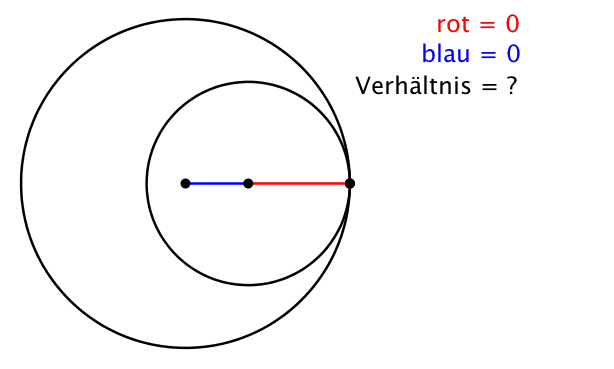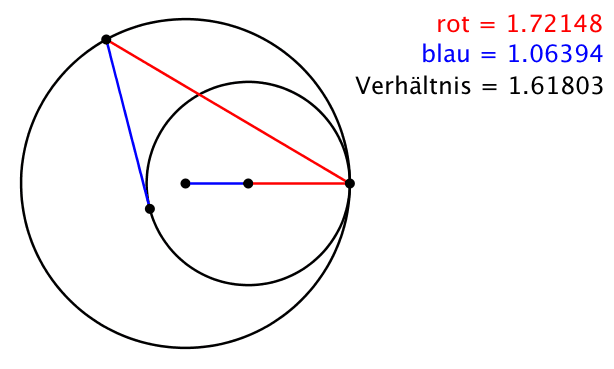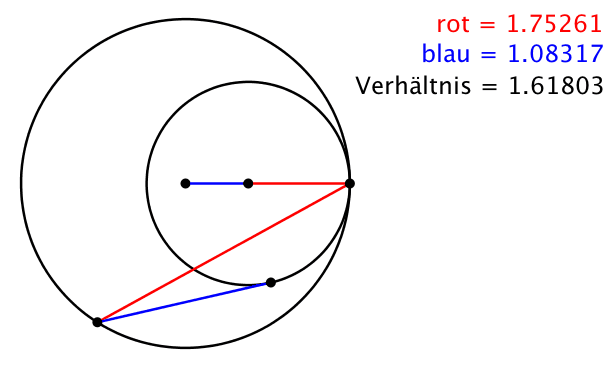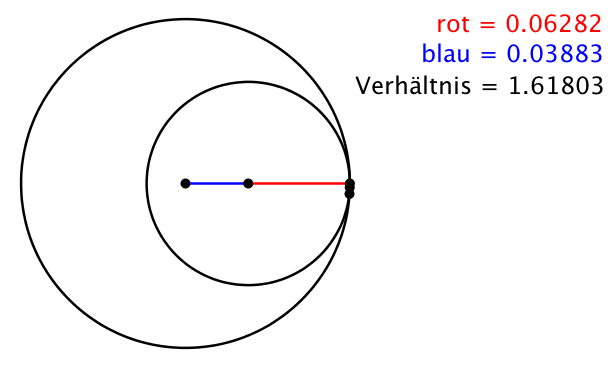
Abb. 5: Der Goldene Schnitt
Weblinks
Stanley Rabinowitz
Literatur
Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.