1 Worum geht es?

Der Goldene Schnitt in Figuren mit einer bestimmten Zerlegungseigenschaft

2 Zerlegungsfiguren

Die Figuren der Abbildung 1 lassen sich jeweils in vier zueinander kongruente und zur Gesamtfigur ähnliche Figuren zerlegen. Die ersten drei Figuren basieren auf einem Dreiecksraster, die zweiten drei auf einem Quadratraster.

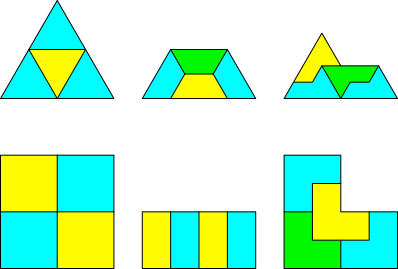
Abb. 1: Zerlegungsfiguren

3 Der Goldene Schnitt

In allen Figuren der Abbildung 1 findet sich nach Einzeichnen eines geeigneten Kreises der Goldene Schnitt. Dabei wird die längere Teilstrecke (Major) jeweils rot, die kürzere (Minor) jeweils blau eingezeichnet.

3.1 Im Dreiecksraster

3.1.1 Gleichseitiges Dreieck

Die Konstruktion des Goldenen Schnittes (Abb. 2) ist klassisch und geht auf George Odom zurück.

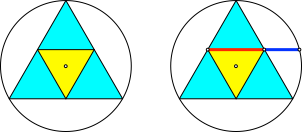
Abb. 2: Konstruktion nach George Odom

3.1.2 Halbes Sechseck

Die Abbildung 3 zeigt ein halbes regelmäßiges Sechseck. Es ist ein gleichschenkliges Trapez mit dem Seitenverhältnis 2:1:1:1. Die Basiswinkel messen 60°.

Abb. 3: Halbes regelmäßiges Sechseck

Die Konstruktion ist eine Variante der Konstruktion von George Odom. Dies kann durch Einzeichnen eines geeigneten gleichseitigen Dreiecks gezeigt werden (Abb. 4).

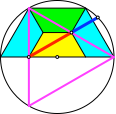
Abb. 4: Beweisfigur

3.1.3 Kirche

In der „Kirchenfigur“ (Abb. 5) sind die hellblauen und die grüne Teilfigur gleichsinnig ähnlich. Die gelbe Teilfigur ist dazu ungleichsinnig ähnlich.

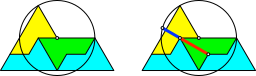
Abb. 5: Der Goldene Schnitt in der Kirche

Auch diese Konstruktion ist eine Variante der Konstruktion nach George Odom (Abb. 6).

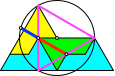
Abb. 6: Beweisfigur

3.2 Im Quadratraster

3.2.1 Quadrat

Bei der Konstruktion im Quadrat (Abb. 7) handelt es sich ebenfalls um ein klassisches Verfahren.

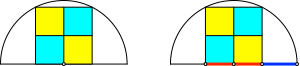
Abb. 7: Konstruktion im Quadrat

3.2.2 Spezielles Rechteck

Das Rechteck ist doppelt so lang wie hoch (Abb. 8).

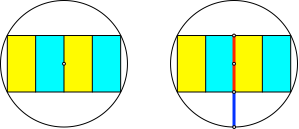
Abb. 8: Spezielles Rechteck

Die Konstruktion ergibt sich aus der Konstruktion im Quadrat (Abb. 9).

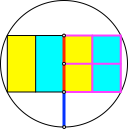
Abb. 9: Beweisfigur

3.2.3 Winkel

Die Grundfigur der Abbildung 10 ist ein aus drei Quadraten zusammengesetzter Winkel.

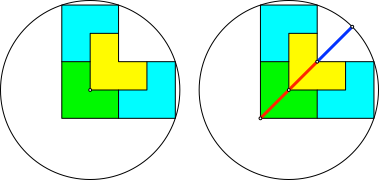
Abb. 10: Der Goldene Schnitt im Winkel

Auch dieses Verfahren ergibt sich aus der Konstruktion im Quadrat (Abb. 11).

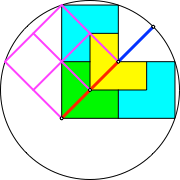
Abb. 11: Beweisfigur

Literatur

Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.