Hans Walser, [20230518]
Goldener Schnitt
Idee und Anregung: Jo Niemeyer, Berlin
1 Worum geht es?
Eine Konstruktion des Goldenen Schnittes. Dynamik
2 Konstruktion
Zum Achsenkreuz zeichnen wir einen Kreis und darauf einen beweglichen Punkt (Abb. 1). Diesen verbinden wir mit dem Zentrum und erhalten so einen roten Zeiger.

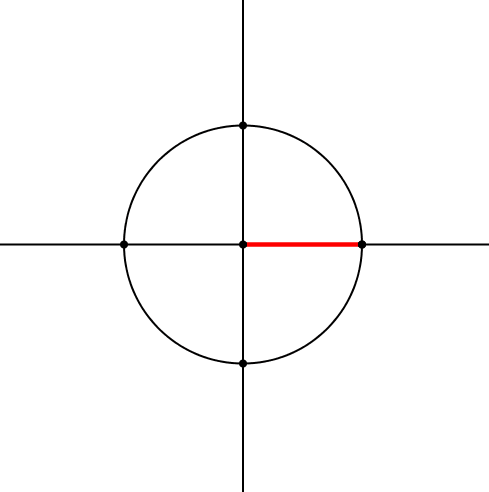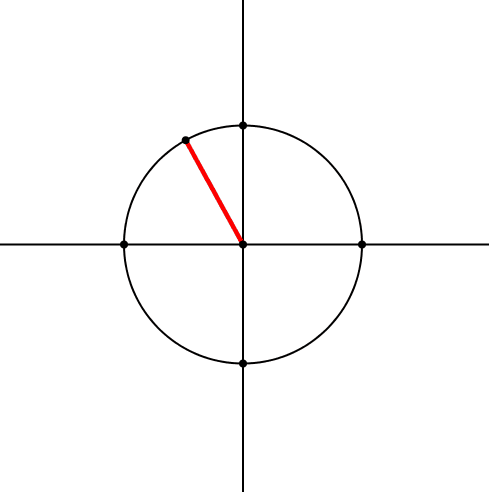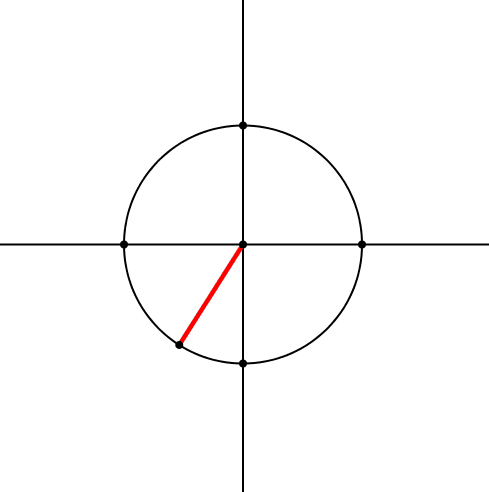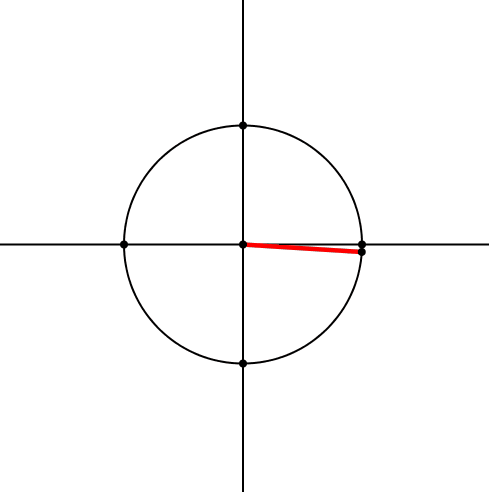
Abb. 1: Kreis mit rotem Zeiger
Auf der Basis des roten Zeigers bauen wir zwei gleichschenklige Dreiecke (Abb. 2). Das eine (grün) hat die Spitze auf der horizontalen Achse, das andere (gelb) auf der vertikalen Achse. Die beiden Dreiecke bilden zusammen, was man in der Schule ein Drachenviereck nennt. Wenn der Zeiger genau auf einer Achse liegt, haben wir einen Halbstreifen.
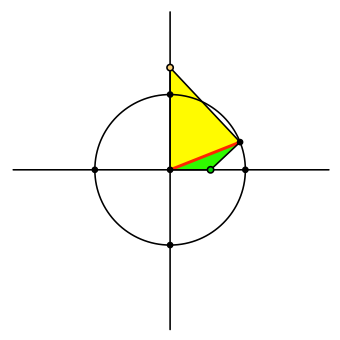
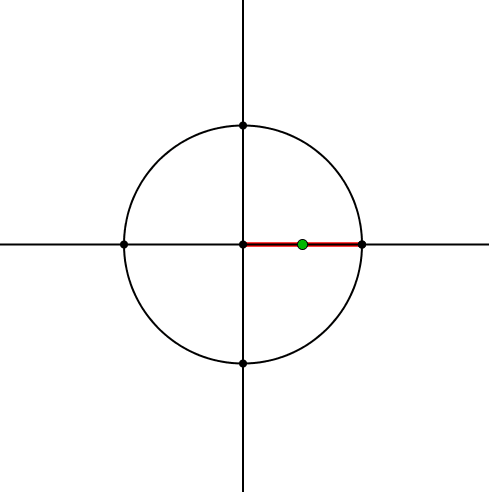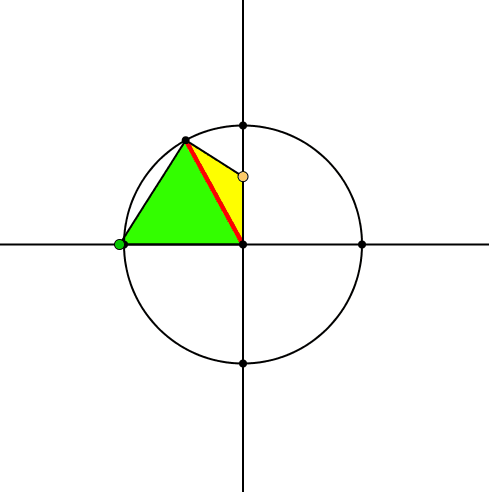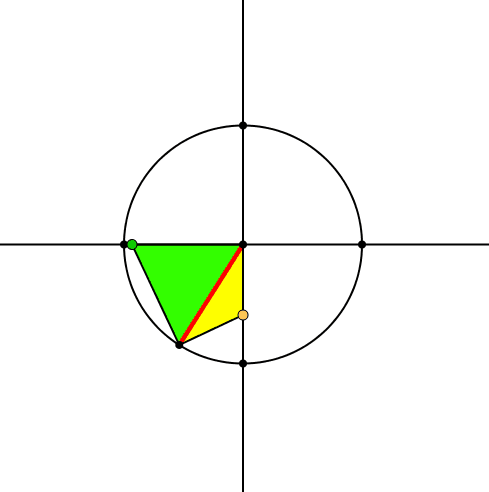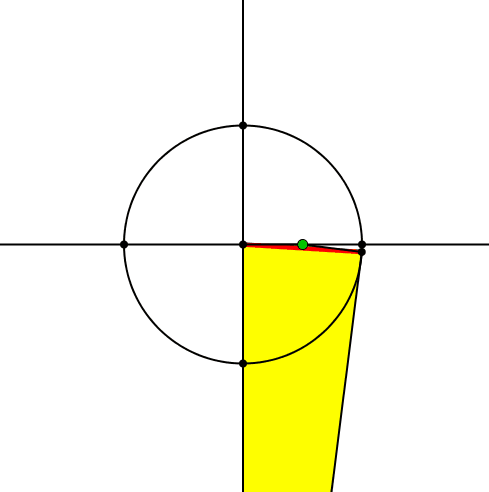
Abb. 2: Zwei gleichschenklige Dreiecke
Nun zeichnen wir um die Spitze des grünen Dreiecks einen grünen Kreis, der durch die Schnittpunkte der vertikalen Achse mit dem Ausgangskreis verläuft (Abb. 3).

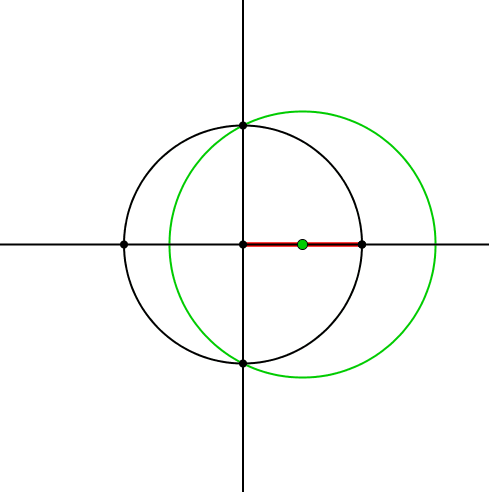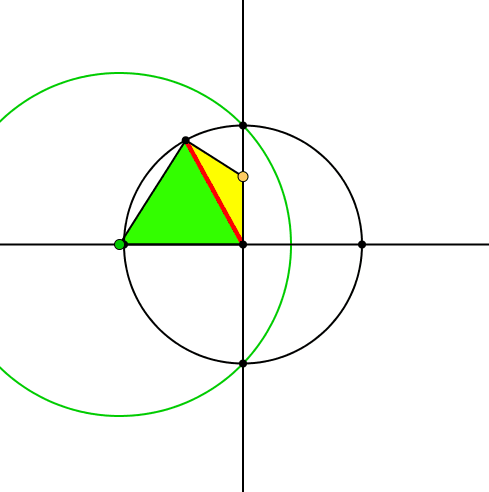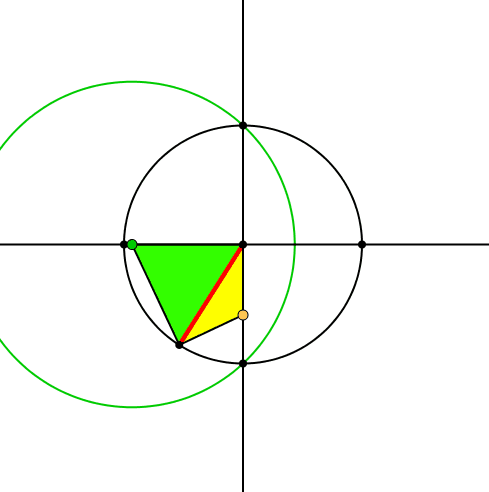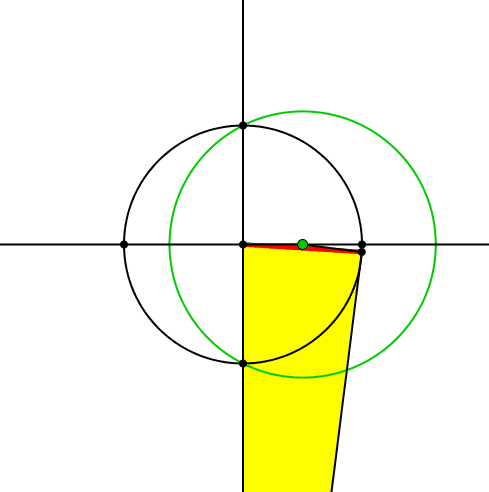
Abb. 3: Grüner Kreis
Entsprechend zeichnen wir um die Spitze des gelben Dreiecks einen gelben Kreis, der durch die Schnittpunkte der horizontalen Achse mit dem Ausgangskreis verläuft (Abb. 4).
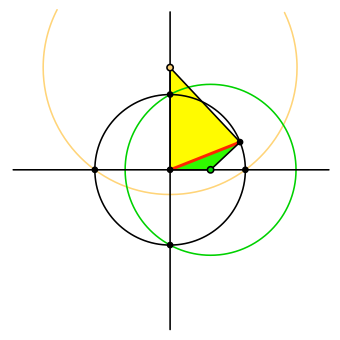
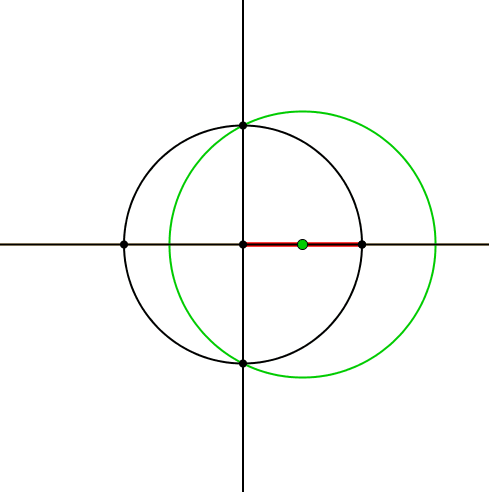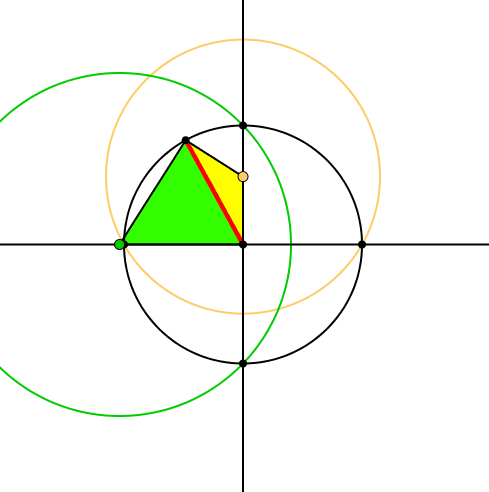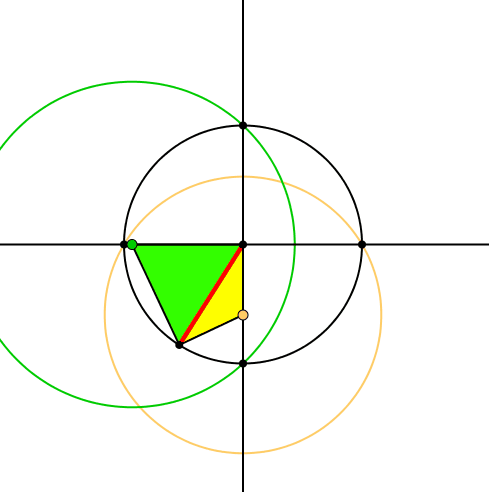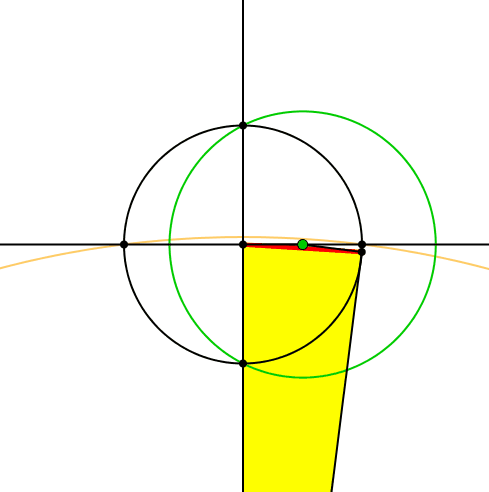
Abb. 4: Gelber Kreis
Die Schnittpunkte des grünen und des gelben Kreises liegen auf der Trägergeraden des roten Zeigers (Abb. 5).
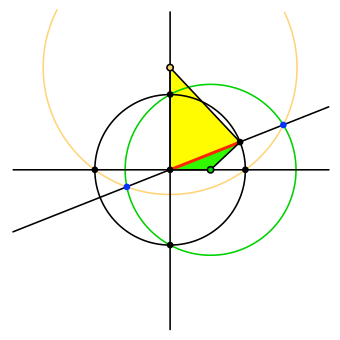
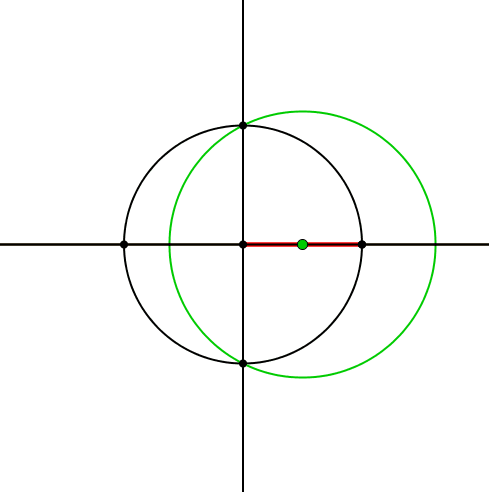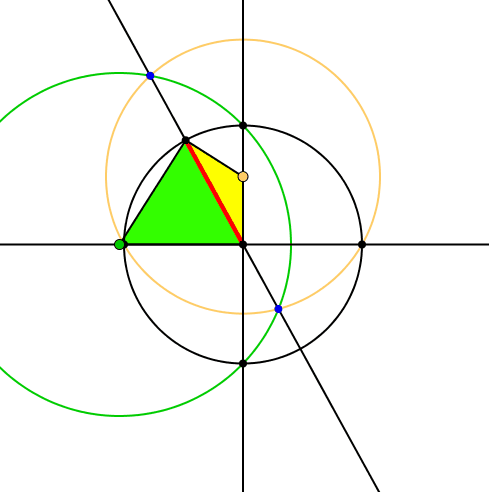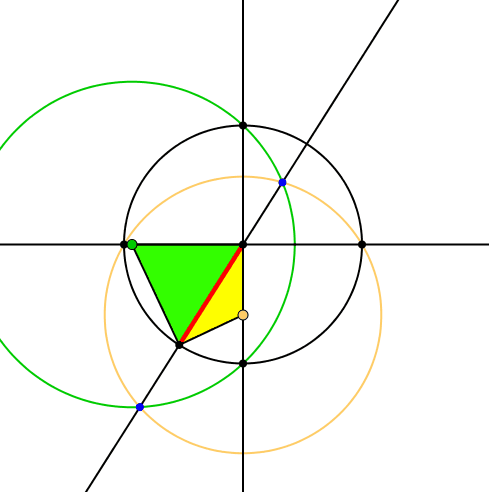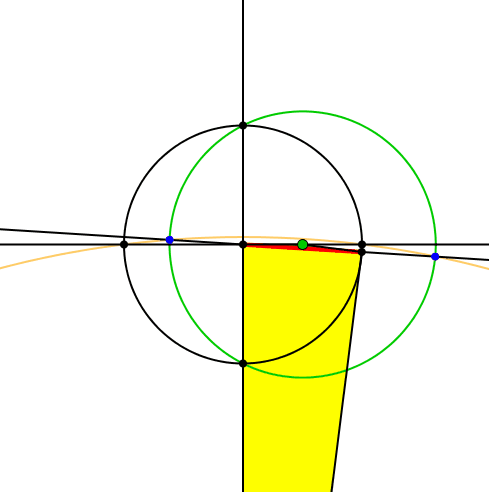
Abb. 5: Schnittpunkte
Mehr noch: die Schnittpunkte führen auf der Trägergeraden des roten Zeigers zu einer Unterteilung im Goldenen Schnitt (Abb. 6). Der rote Zeiger ist der Major, die beiden äußeren Abschnitte sind Minore (blau). Beweis durch Nachrechnen.
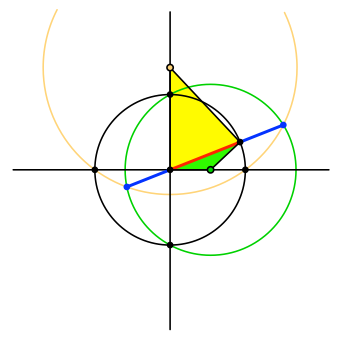
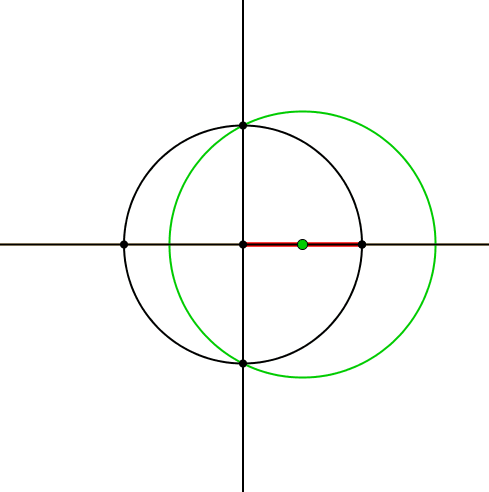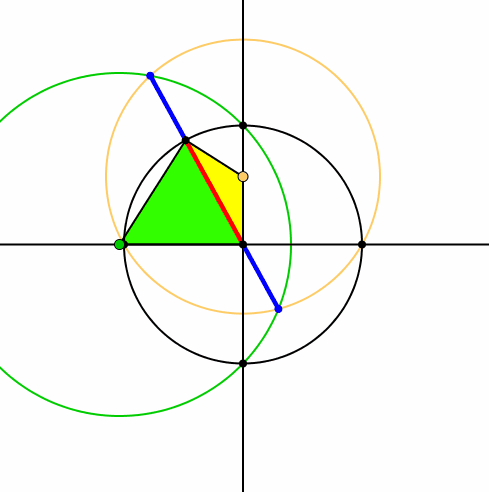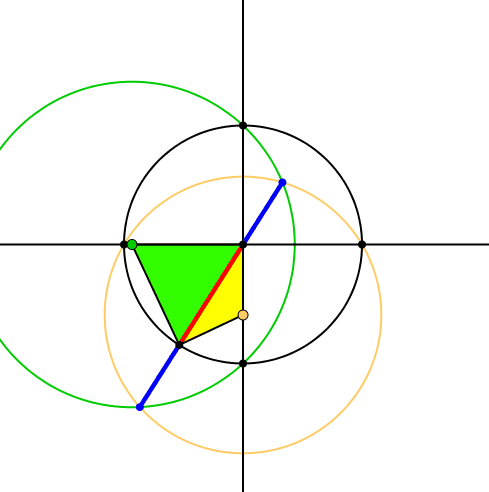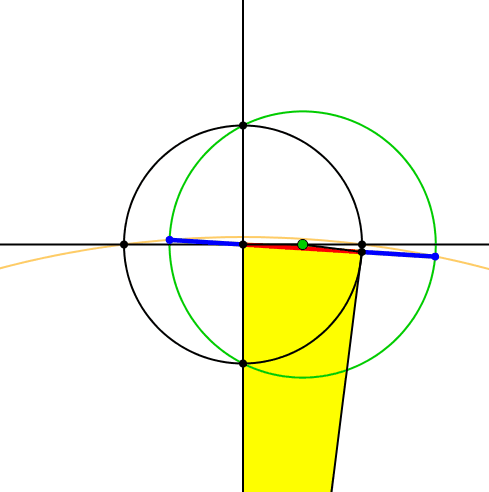
Abb. 6: Goldener Schnitt
Die Schnittpunkte bewegen sich je auf einem Kreis (Abb. 7 und 8).
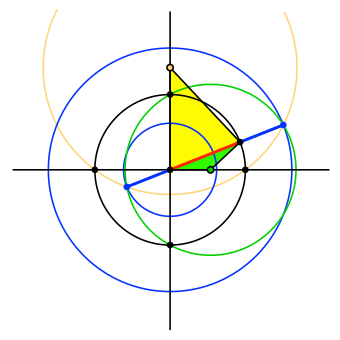
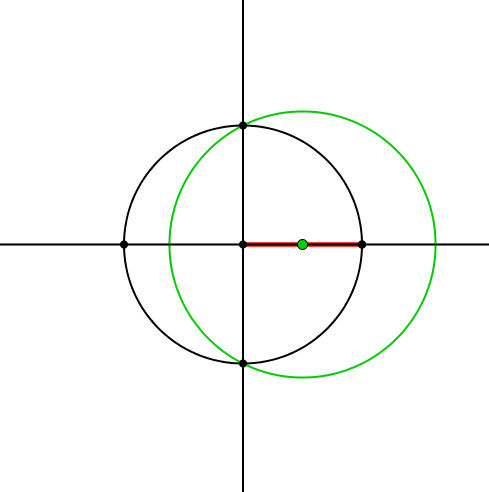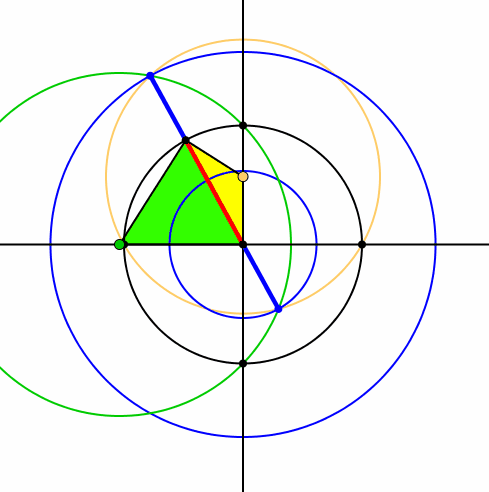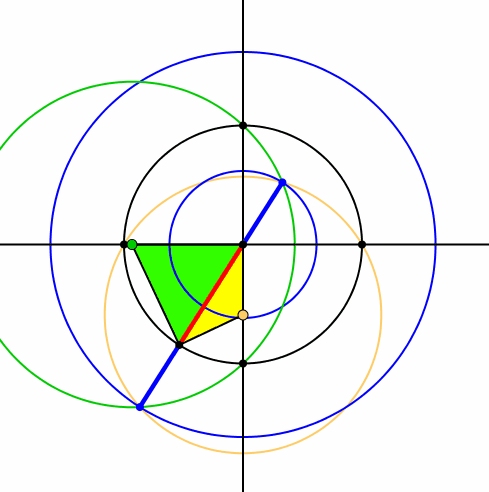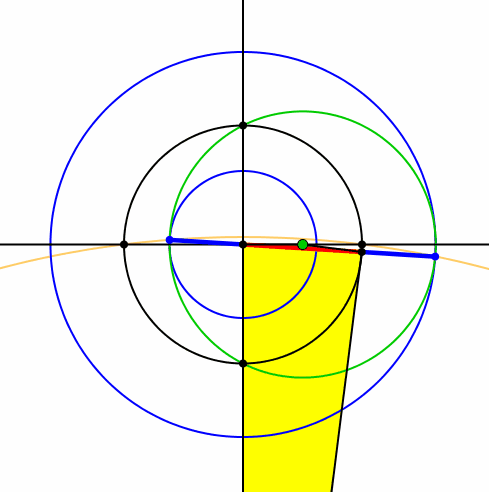
Abb. 7: Schnittpunkte auf Kreisen
Die beiden Kreise sind konzentrisch zum Ausgangskreis (Abb.8).

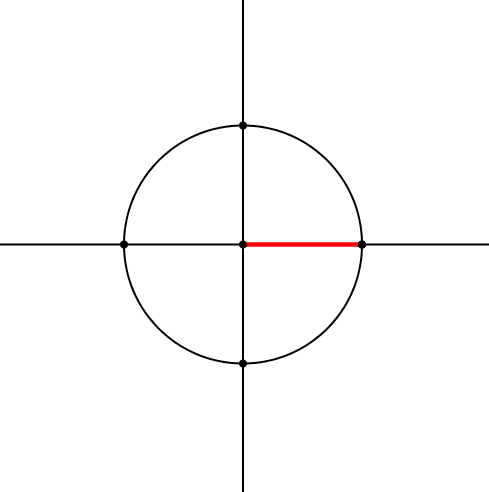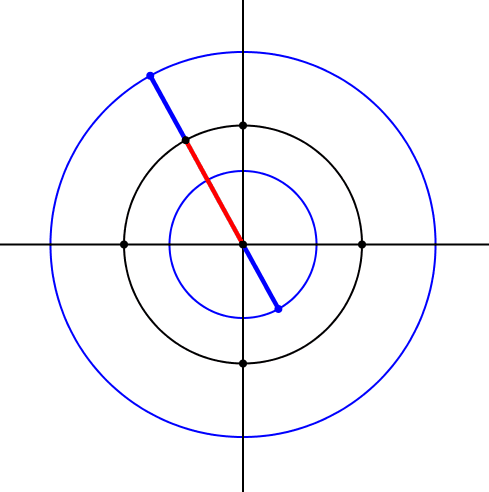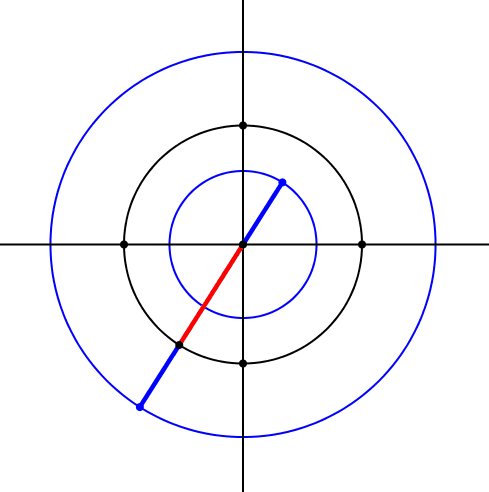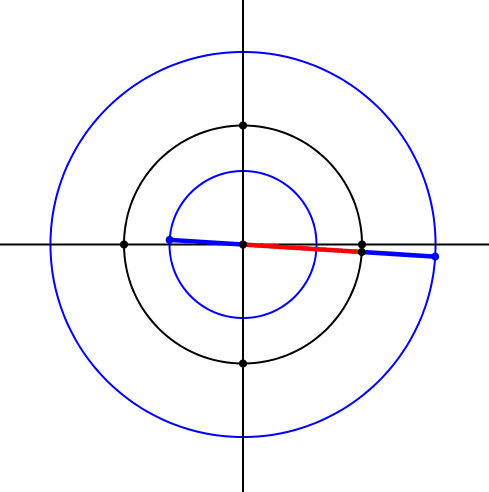
Abb. 8: Drei konzentrische Kreise
Der kleine und der mittlere Kreis passen in den großen (Abb. 9). Es entsteht der Goldene Arbelos.


Abb. 9: Passt. Goldener Arbelos
Weblinks
Hans Walser: Der Goldene Schnitt
http://www.walser-h-m.ch/hans/Miniaturen_Uebersicht/Goldener_Schnitt/index.html
Hans Walser: Schnittpunkte
http://www.walser-h-m.ch/hans/Schnittpunkte/