1 Konstruktion

In einem beliebigen rechtwinkligen Dreieck zeichnen wir die Mittelpunkte der beiden Katheten (Abb. 1).

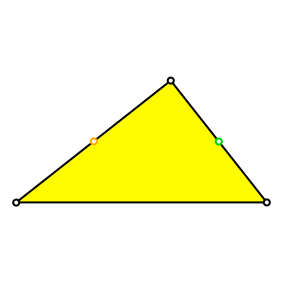
Abb. 1: Mittelpunkte der Katheten

Dann tragen wir die senkrecht auf der Hypotenuse stehende Höhe auf die Katheten ab (Abb. 2).

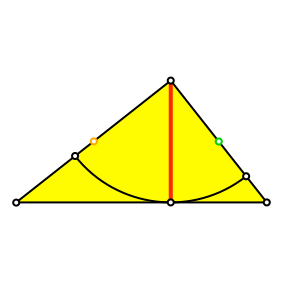
Abb. 2: Höhe abtragen

Weiter zeichnen wir einen Kreis um den Mittelpunkt der einen Kathete durch den mit der Höhe abgetragenen Punkt auf der anderen Kathete (Abb. 3). Entsprechend verfahren wir mit der zweiten Kathete.

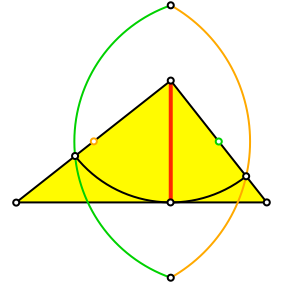
Abb. 3: Kreise

Die Schnittpunkte der beiden Kreise liegen auf der verlängerten Dreieckshöhe und unterteilen diese im Verhältnis des Goldenen Schnittes (Abb. 4).

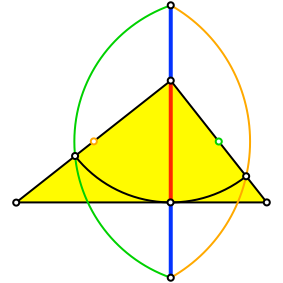
Abb. 4: Schnittpunkte

Die Dreieckshöhe ist der Major, die angesetzten Abschnitte sind Minore (Abb. 5).

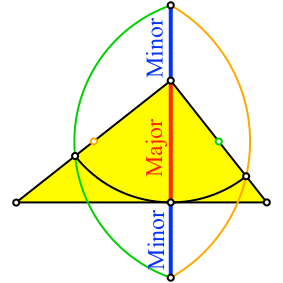
Abb. 5: Minor-Major-Minor

2 Variation des Dreieckes

Da die Konstruktion für ein beliebiges rechtwinkliges Dreieck gilt, können wir die Ecke mit dem rechten Winkel auf dem Thaleskreis variieren (Abb. 6).

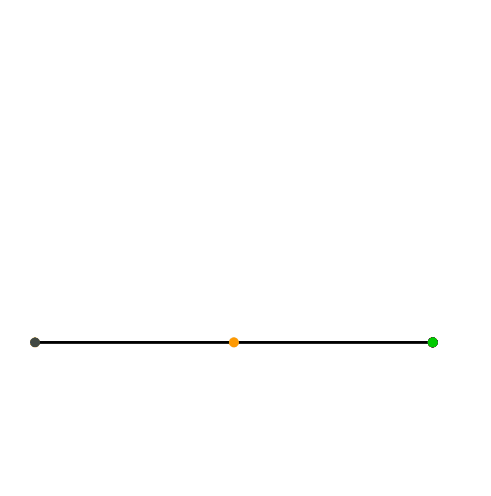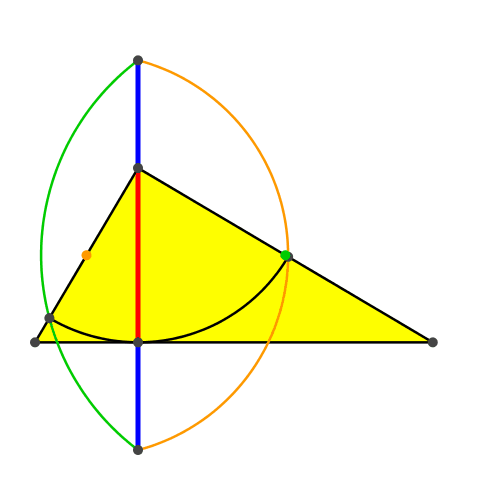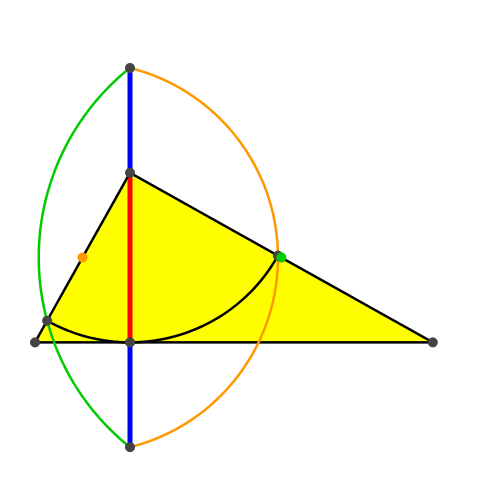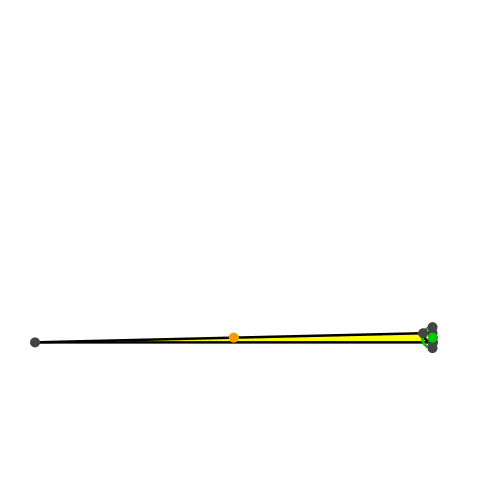
Abb. 6: Variation des rechtwinkligen Dreieckes

3 Beweis

Der Beweis erfolgt rechnerisch. Wir arbeiten mit der Beweisfigur der Abbildung 7. Die Höhe setzen wir 1, der Hypotenusenabschnitt p vom Höhenfußpunkt H zur Ecke A ist variabel.

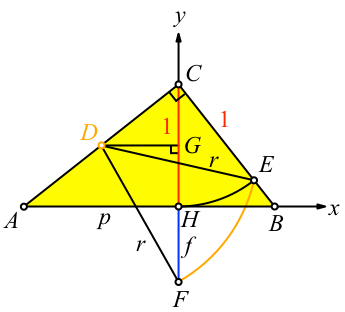
Abb. 7: Beweisfigur

Der Punkt D hat als Mittelpunkt der Strecke AC die Koordinaten (-p/2, ½). Für den Abschnitt CD erhalten wir:

|CD|² = ¼*(p² + 1)

Das Dreieck CDE ist rechtwinklig und hat nach Konstruktion die Kathete |CE| = 1. Somit erhalten wir für r:

r² = |CD|² + 1 = ¼*p² + 5/4

Wir schneiden die Höhengerade mit dem Kreis um D durch E. Der Schnittpunkt F hat die Koordinaten (0, –f), wobei f noch unbekannt ist.

Das Dreieck DFG ist ebenfalls rechtwinklig und hat die Katheten ½*p und ½ + f. Damit ergibt sich für r:

r² = ¼*p² + (½ + f)²

Gleichsetzen der beiden Informationen über r liefert:

¼*p² + 5/4 = ¼*p² + (½ + f)²

Wir sehen, dass die variable Größe p „herausfällt“. Übrig bleibt die quadratische Gleichung:

f² + f – 1 = 0

Diese Gleichung hat die Lösungen –Φ und +1/Φ, wobei Φ der Goldene Schnitt ist:

Φ = (1 + √5)/2

Wenn wir nun dieselben Überlegungen für die andere Kathete des ursprünglichen rechtwinkligen Dreiecks durchführen, kommen wir zum selben Punkt F. Der untere Schnittpunkt der beiden Kreise gemäß Konstruktion (Abb. 3) liegt also tatsächlich auf der Geraden durch die Höhe und liefert den Minor gegenüber der Höhe.

Aus Symmetriegründen (Parallele zur Hypotenuse auf halber Dreieckshöhe als Symmetrieachse) gilt das auch für den oberen Schnittpunkt.

4 Sonderfall

Im Sonderfall eines gleichschenklig rechtwinkligen Dreiecks ergibt sich die Figur der Abbildung 8. Wir können zusätzlich ein Quadrat einpassen.

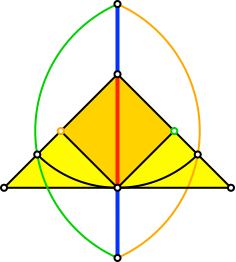
Abb. 8: Sonderfall

Weblinks

Hans Walser: Miniaturen: Goldener Schnitt

http://www.walser-h-m.ch/hans/Miniaturen_Uebersicht/Goldener_Schnitt/index.html