1 Worum es geht

Konstruktion des Goldenen Schnittes mit Inkreisen und Kegelschnitten.

Link zu einem pythagoreischen Dreieck.

2 Inkreise

In einem aus zwei Quadraten zusammengesetzten Rechteck zeichnen wir eine Diagonale (Abb. 1).

Abb. 1: Diagonale im Doppelquadrat

Diese Diagonale unterteilt das Rechteck in zwei rechtwinklige Dreiecke. In jedem dieser Dreiecke zeichnen wir den Inkreis (Abb. 2).

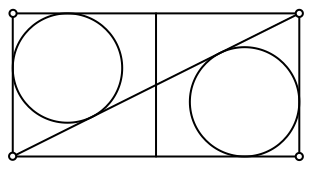
Abb. 2: Inkreise

Die Berührungspunkte der Inkreise auf der Diagonalen unterteilen diese im Goldenen Schnitt in der Reihenfolge Minor-Major-Minor (Abb. 3). Nachweis rechnerisch.

Abb. 3: Goldener Schnitt

Der Major ist gleich lang wie die Quadratseite.

3 Hyperbel

Wir zeichnen wiederum in einem aus zwei Quadraten zusammengesetzten Rechteck eine Diagonale ein (Abb. 4).

Abb. 4: Diagonale im Doppelquadrat

Und nun zeichnen wir die Hyperbel mit beiden Hyperbelästen, welche die Endpunkte der Diagonalen als Brennpunkte hat und durch eine der beiden weiteren Ecken des Rechteckes verläuft (Abb. 5). Aus Symmetriegründen verläuft die Hyperbel dann auch durch die vierte Ecke des Rechtecks.

Abb. 5: Hyperbel

Die Hyperbel unterteilt die Diagonale im Goldenen Schnitt in der Reihenfolge Minor-Major-Minor (Abb. 6). Nachweis rechnerisch.

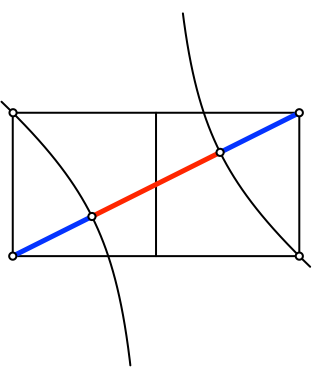
Abb. 6: Goldener Schnitt

Der Major ist gleich lang wie die Quadratseite.

4 Hyperbel und Ellipse

In ein aus zwei Quadraten gebildetes Rechteck zeichnen wir eine Gerade durch zwei gegenüberliegende Eckpunkte (Abb. 7).

Abb. 7: Diagonale Gerade

Nun zeichnen wir eine Hyperbel und eine Ellipse mit diesen beiden Eckpunkten als Brennpunkten durch die beiden anderen Ecken des Rechteckes (Abb. 8).

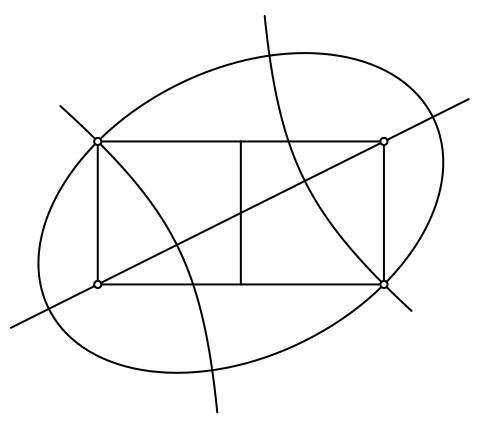
Abb. 8: Hyperbel und Ellipse

Diese beiden Kegelschnitte schneiden aus der diagonalen Geraden Abschnitte im Goldenen Schnitt heraus (Abb. 9).

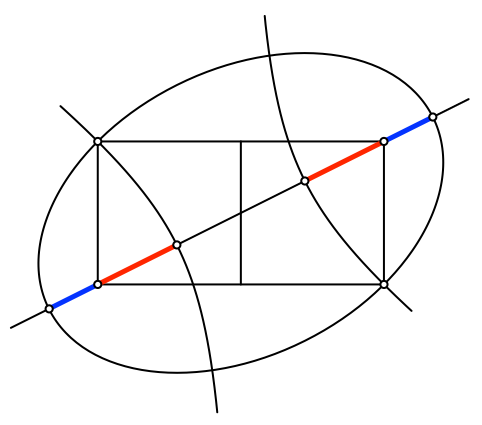
Abb. 9: Goldener Schnitt

5 Pythagoreisches Dreieck

Die vier Schnittpunkte der beiden Kegelschnitte bilden ein Rechteck mit dem Seitenverhältnis 4:3 (Abb. 10).

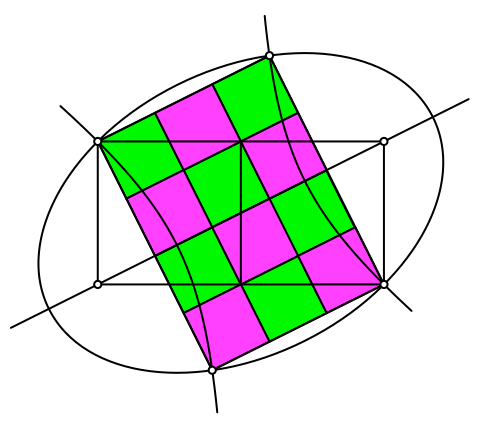
Abb. 10: Rechteck 4:3

Wir können dieses Rechteck mit einer Diagonalen (zum Beispiel der zweiten Diagonalen des ursprünglichen aus zwei Quadraten bestehenden Recktecks) in zwei rechtwinklige Dreiecke zerlegen (Abb. 11). Diese haben das Seitenverhältnis 3:4:5. Es handelt sich hier um das einfachste pythagoreische Dreieck.

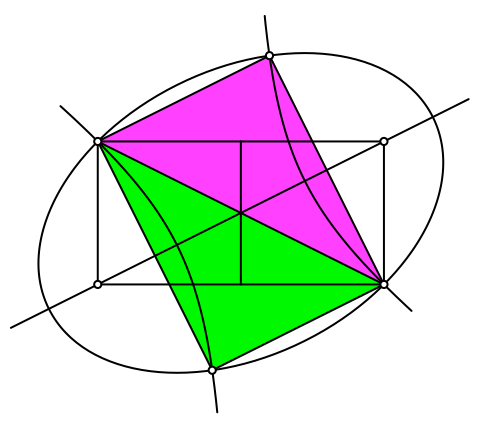
Abb. 11: Pythagoreische Dreiecke

Literatur

Walser, Hans (2024): Der Goldene Schnitt. Geometrische und zahlentheoretische Betrachtungen. 7. Auflage. Springer Spektrum.
Print-ISBN 978-3-662-68556-3. E-Book_ISBN 978-3-662-68557-0.
https://doi.org/10.1007/978-3-662-68557-0