Hans Walser, [20180515a]
Goldenes Dreieck
1 Worum geht es?
Unter dem Goldenen Dreieck verstehen wir das gleichschenklige Dreieck mit dem Spitzenwinkel 36ˇ (Walser 2013, S. 43).
Das Goldene Dreieck zusammen mit seinem Umkreis scheidet aus gewissen, zur Basis parallelen Geraden Strecken im VerhŠltnis des Goldenen Schnittes heraus.
2 Der klassische Fall
Die Seiten des regulŠren Pentagramms (Abb. 1a) schneiden sich unter VerhŠltnissen des Goldenen Schnittes. Daraus ergibt sich fźr das Goldene Dreieck und seinen Umkreis eine zur Basis parallele Gerade, welche ebenfalls Strecken im VerhŠltnis des Goldenen Schnittes enthŠlt. Die Reihenfolge ist Major-Minor-Major.
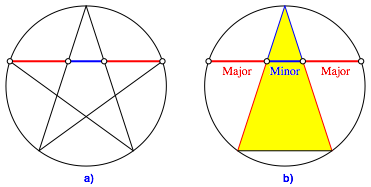
Abb. 1: Goldener Schnitt im Pentagramm
3 Umgekehrte Reihenfolge
In welcher Position der zur Basis parallelen Geraden ergibt sich eine Unterteilung in der Reihenfolge Minor-Major-Minor?
Die Lšsung ergibt sich durch Spiegelung der Geraden in der Abbildung 1 am Umkreismittelpunkt (Abb. 2a). Nachweis durch Rechnung.
Der Major in auf der unteren Geraden ist grš§er als die Majore auf der oberen Geraden. Auch die Minore auf der unteren Geraden sind grš§er als der Minor auf der oberen Geraden.
Die Figur lŠsst sich in ein regulŠres Zehneck einpassen (Abb. 2b).
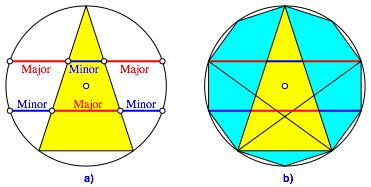
Abb. 2: Umgekehrte Reihenfolge
Literatur
Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing źber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.