Hans Walser, [20120904]

Grenzpunkte im DIN-Rechteck

Die Rechtecke des DIN-Systems werden zur Visualisierung von Grenzpunkten (Limespunkten) eingesetzt. Zu gegebenen Grenzpunkten kann dabei eine passende Zerlegung des A0-Rechtecks konstruktiv gefunden werden.

Der Hintergrund ist die Dualbruchzerlegung einer reellen Zahl.

1        Zerlegung

Wir denken uns ein A0-Rechteck im Hochformat, das wir durch Halbieren schrittweise unterteilen. Es entsteht eine Folge von Rechtecken A1 (Querformat), A2 (Hochformat), A3 (Querformat), ... , welche das A0-Rechteck ausschšpfen.

In der Regel wird das gemŠ§ Abbildung 1 dargestellt.

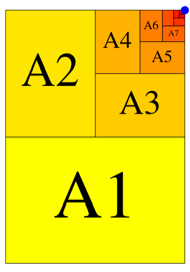
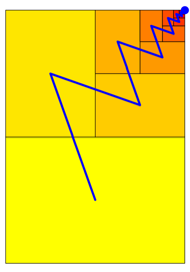
Abb. 1: Folge von DIN-Rechtecken

Wir kšnnen die Reihenfolge auch durch Verbindungslinien der Mittelpunkte aufeinander folgender Rechtecke grafisch darstellen.

Rechts oben haben wir den Grenzpunkt. Der Reihenfolgen-Graf mŸndet in den Grenzpunkt.


2        Spiralfšrmige Anordnung

Die Rechtecke kšnnen auch spiralfšrmig angeordnet werden (Abb. 2).

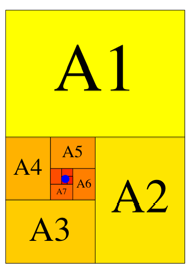
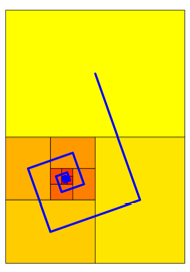
Abb. 2: Spiralfšrmige Anordnung

Der Grenzpunkt liegt nun im Innern der Figur. Im Koordinatensystem der Abbildung 3 hat er die Koordinaten .

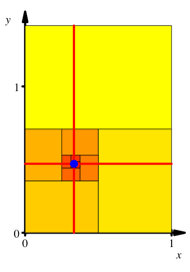
Abb. 3: Koordinaten

Diese Koordinaten kšnnen wie folgt berechnet werden.

Die horizontale Gerade durch den Grenzpunkt trifft genau die Rechtecke im Hochformat. Diese haben die Breiten . In unserem Spiralenbeispiel lesen wir fŸr die x-Koordinate des Grenzpunktes ab:

Die vertikale Gerade durch den Grenzpunkt trifft genau die Rechtecke im Querformat. Diese haben die Hšhen . In unserem Spiralenbeispiel lesen wir fŸr die y-Koordinate des Grenzpunktes ab:


3        Beliebiger Grenzpunkt

Es gilt:

Die Teilrechtecke kšnnen so angeordnet werden, dass ein beliebig im Innern oder auf dem Rand des A0-Rechteckes vorgegebener Punkt als Grenzpunkt erscheint.

ZunŠchst einige Beispiele.

3.1      Beispiele

3.1.1     Mittelpunkt als Grenzpunkt

In der Abbildung 4 ist der Mittelpunkt der Grenzpunkt.

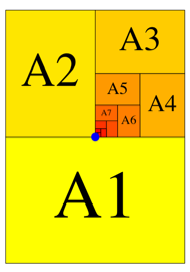
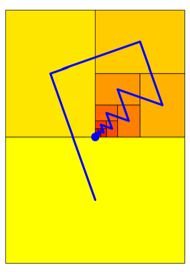
Abb. 4: Mittelpunkt als Grenzpunkt

Etwas irritierend ist zunŠchst, dass die Zerlegung keine Mittelpunktssymmetrie hat. Das kann es aber auch nicht geben, da jedes Teilrechteck genau einmal vorkommt.


3.1.2     FŸnftel und Siebtel

Der Grenzpunkt der Abbildung 5 hat die Koordinaten .

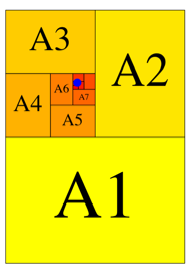
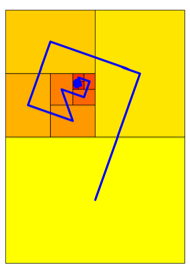
Abb. 5: FŸnftel und Siebtel

3.1.3     Goldener Schnitt

Mit den Grenzpunktkoordinaten erhalten wir den Goldenen Schnitt am oberen Rand (Abb. 6).

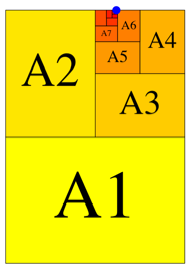
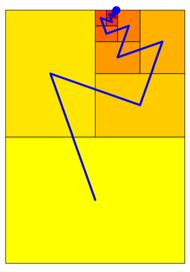
Abb. 6: Goldener Schnitt

3.1.4     Hinkende Spirale

In der Abbildung 7 haben wir den Grenzpunkt .

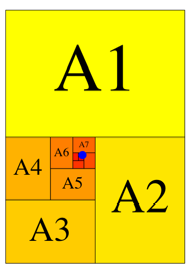
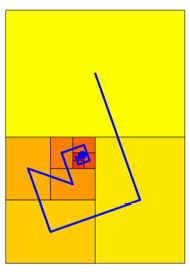
Abb. 7: Hinkende Spirale

3.2      Allgemeines Vorgehen

3.2.1     Auf Katzenpfoten

Wir illustrieren das konstruktive Vorgehen am Beispiel mit den Grenzpunktkoordinaten in mehreren Schritten (Abb. 8).

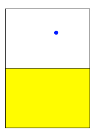
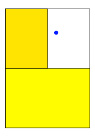
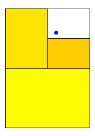
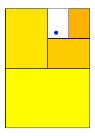
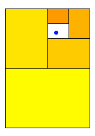
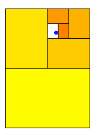
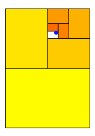
Abb. 8: Konstruktives Vorgehen

Wir sehen, wie die Katze um den hei§en Brei herumschleicht.

Der anvisierte Grenzpunkt liegt bei diesem Verfahren immer in einem wei§en Restrechteck, welches aber auch DIN-Format hat. Dann wird jeweils diejenige HŠlfte des Restrechtecks mit einem Teilrechteck zugedeckt, welche den Grenzpunkt nicht enthŠlt.


3.2.2     Sonderfall

Falls der Grenzpunkt genau auf eine horizontale oder vertikale Mittelparallele des wei§en Restrechtecks zu liegen kommt, decken wir die untere beziehungsweise linke HŠlfte des Restrechtecks zu. Dies ist ein WillkŸrentscheid, der nicht begrŸndet werden muss. Man kšnnte es auch anders machen. Die Abbildung 9 illustriert dies fŸr den Grenzpunkt .

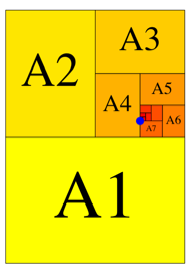
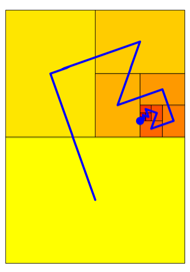
Abb. 9: Grenzpunkt auf dem Rand eines Teilrechteckes

 

Auch das Beispiel mit dem Mittelpunkt als Grenzpunkt (Abb. 4) illustriert das Vorgehen in diesem Sonderfall.

Allgemein tritt dieser Sonderfall genau dann auf, wenn der Grenzpunkt die Koordinaten mit oder oder beides hat.

4        Hintergrund

GemŠ§ unserem konstruktiven Vorgehen liegen alle querformatigen Teilrechtecke entweder oberhalb oder unterhalb des Grenzpunktes. Eine horizontale Gerade durch den Grenzpunk durchschneidet also nur Teilrechtecke im Hochformat. Die Teilrechtecke im Hochformat haben die Breiten . Die x-Koordinate des Grenzpunktes setzt sich also aus einer Auswahl von Summanden aus zusammen. Die Auswahl ergibt sich durch die Dualbruchentwicklung der x-Koordinate.

Analog wird fŸr die y-Koordinate Ÿberlegt. Dabei muss der Skalierungsfaktor weggelassen werden.

Beispiel mit den Grenzpunktkoordinaten (Abb. 10).

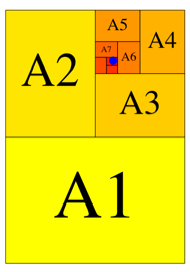
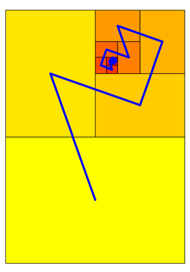
Abb. 10: Illustrationsbeispiel

Dualbruchzerlegungen:

 

Dualbruch von 0.6 = 0. 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1

Dualbruch von 0.8 = 0. 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0

 

Im Dualbruch von 0.6 steht hinter dem Dualpunkt eine 1. Dies beideutet, dass das erste Teilrechteck im Hochformat, also A2, links vom Grenzpunkt liegt. Die beiden nachfolgenden Nullen in der Dualbruchzerlegung bedeuten, dass die beiden folgenden Teilrechtecke im Hochformat, also A4 und A6, rechts vom Grenzpunkt liegen. Das grš§ere der beiden Rechtecke, also A4, liegt nŠher beim Au§enrand des Ausgangsrechteckes A0. Weiter sind A8 und A10 links vom Grenzpunkt, A12 und A14 wieder rechts und so weiter. Da 0.6 eine rationale Zahl ist, haben wir ein periodisches Verhalten.

FŸr die y-Koordinate lŠuft die †berlegung entsprechend.

Bei abbrechendem Dualbruch (Abb. 4 und Abb. 9) kommt der Grenzpunkt auf den Rand eines Teilrechteckes zu liegen.

Unsere Ausschšpfungen des A0-Rechteckes sind also auch Visualisierungen der Dualbruchzerlegung der x-Koordinate und der y-Koordinate.