Hans Walser, [20230618]

Großes Dodekaeder

1 Worum es geht

Auf- und Abwickeln des großen Dodekaeders

2 Das große Dodekaeder

Das große Dodekaeder finden wir wie folgt. Wir beginnen mit dem Kantengerüst des regelmäßigen Ikosaeders (Abb. 1).

Abb. 1: Kantengerüst des regelmäßigen Ikosaeders

Durch Einpassen von 20 regelmäßigen Dreiecken ergäbe sich das Ikosaeder. Wir können stattdessen aber auch regelmäßige Fünfecke einpassen. Die Abbildung 2 zeigt ein Beispiel.

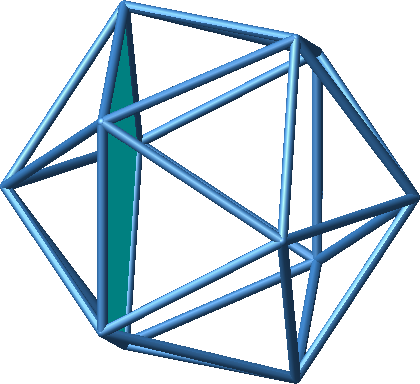
Abb. 2: Regelmäßiges Fünfeck

Es gibt insgesamt zwölf Möglichkeiten, ein Fünfeck einzupassen (Abb. 3 und 4). Überlegungstipp: die Fünfecke können mit der naheliegenden Ikosaederecke zu einer fünfseitigen Pyramide ergänzt werden.

Die Fünfecke durchdringen sich gegenseitig. Die entstehende Figur ist das große Dodekaeder.

Abb. 3: Großes Dodekaeder

Abb. 4: Großes Dodekaeder von allen Seiten

3 Abwicklung

3.1 Gewöhnliches Dodekaeder

Ich habe mir lange überlegt, wie die Abwicklung des großen Dodekaeders aussehen kann. Die Abbildung 5 zeigt eine klassische Abwicklung des gewöhnlichen Dodekaeders. Auf der einen Seite gelb, auf der anderen blau. Die Abwicklung besteht aus zwei Rosetten mit einem zentralen Fünfeck und darum herum fünf weiteren Fünfecken. Die beiden Rosetten sind an einer äußeren Kante (rot in Abb. 5) verheftet.

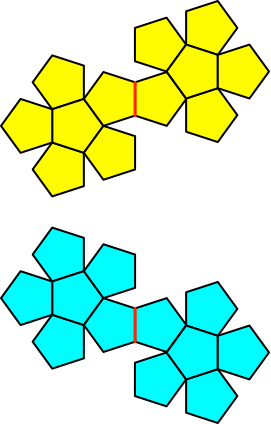
Abb. 5: Abwicklung des gewöhnlichen Dodekaeders

Leider kann diese Abwicklung nicht (auch nicht virtuell mit Selbstdurchdringung) zum großen Dodekaeder aufgewickelt werden. Es treten Überlappungen von Fünfecken auf, weshalb dann andernseits Fünfecke fehlen (Abb. 6).

Abb. 6: Aufwickeln des gewöhnlichen Dodekaeders

3.2 Großes Dodekaeder

Der Trick besteht darin, dass wir die Verheftung der beiden Rosetten an „Innenkanten“ vornehmen müssen (Abb. 7).

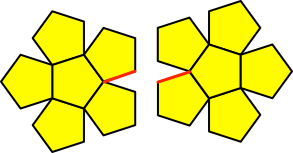
Abb. 7: Innenkanten

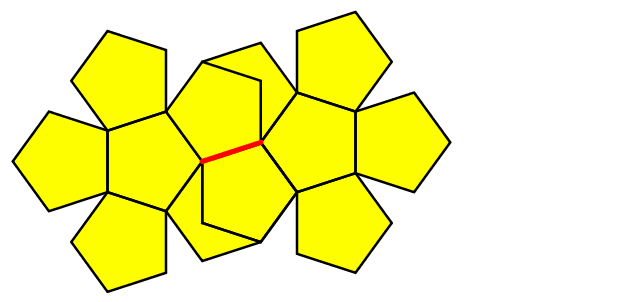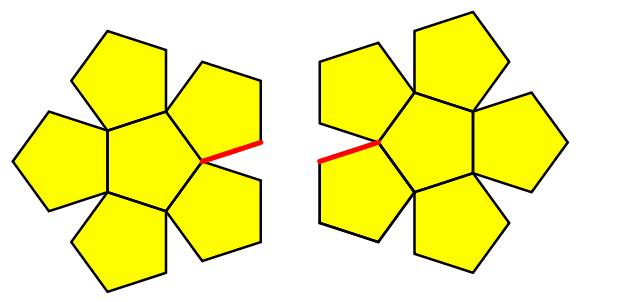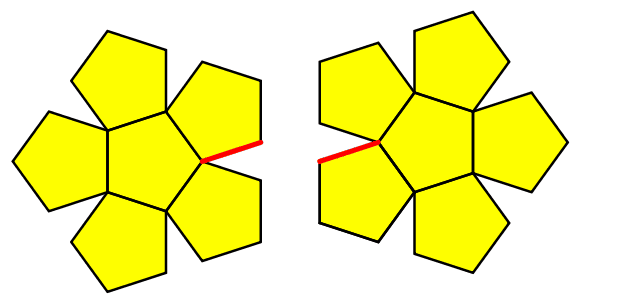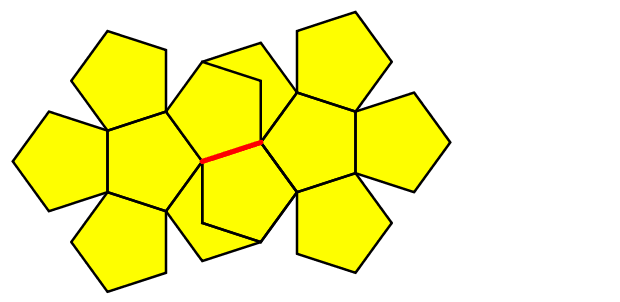
Abb. 8: Verheftung an Innenkanten

Dabei überlappen sich die beiden Rosetten (Abb. 9). Die Abwicklung kann also nicht aus einem einzigen Blatt Papier herausgeschnitten werden.

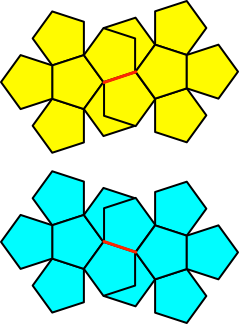
Abb. 9: Überlappende Rosetten

Dafür funktioniert die Aufwicklung (Abb. 10). Wir sehen aber, dass in der Situation des gewöhnlichen Dodekaeders zwei Fünfecke fehlen, da wir andernorts Überlappungen haben.

Abb. 10: Aufwicklung

Weblinks

Hans Walser: Dodekaederdurchwicklung

http://www.walser-h-m.ch/hans/Miniaturen/D/Dodekaederdurchwicklung2/Dodekaederdurchwicklung2.html

Hans Walser: Dodekaederdurchwicklung

http://www.walser-h-m.ch/hans/Miniaturen/D/Dodekaederdurchwicklung/Dodekaederdurchwicklung.html

Hans Walser: Ikosaederdurchwicklung

http://www.walser-h-m.ch/hans/Miniaturen/I/Ikosaederdurchwicklung/Ikosaederdurchwicklung.html

Hans Walser: Oktaederdurchwicklung

http://www.walser-h-m.ch/hans/Miniaturen/O/Oktaederdurchwicklung/Oktaederdurchwicklung.html

Hans Walser: Tetraederdurchwicklung

http://www.walser-h-m.ch/hans/Miniaturen/T/Tetraederdurchwicklung/Tetraederdurchwicklung.html

Hans Walser: Würfeldurchwicklungen

http://www.walser-h-m.ch/hans/Miniaturen/W/Wuerfeldurchwicklungen/Wuerfeldurchwicklungen.html