Hans Walser, [20100524a]
Zwischen ggT und kgV
1
Motivation
In der Schule lernte
man den Satz, dass das Produkt zweier Zahlen gleich dem Produkt ihres grš§ten
gemeinsamen Teilers (ggT) mit ihrem kleinsten gemeinsamen Vielfachen (kgV) ist:
![]()
Und dann kam der
erhobene Zeigefinger: Gilt aber nicht fźr drei Zahlen. — Mich hat das als
Schźler irritiert.
2
Beispiel mit drei Zahlen
Rechnen wir mal mit ![]() ,
, ![]() und
und ![]() .
.
2.1
ggT und kgV
Fźr ggT und kgV erhalten wir:
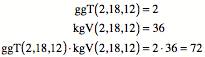
Andererseits ist:
![]()
Nun haben wir:
![]()
Auf der linken Seite
des Ungleichheitszeichens ăfehltŇ ein Faktor 6. Was hat es damit auf sich?
2.2
Turnźbungen
Wir rechnen paarweise
das kgV und anschlie§end den ggT der drei kgV:
![]()
Nun machen wir es
umgekehrt:
![]()
Wir kommen bei beiden
Verfahren auf die ăfehlendeŇ Zahl 6.
2.3
Primfaktorzerlegungen
Wir arbeiten mit der
Primfaktorzerlegung:
![]()
Es ist:
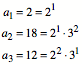
Wir tabellieren die
Exponenten; falls eine Primzahl nicht als Primfaktor vorkommt, schreiben wir den Exponenten null.
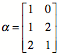
Nach dem in der Schule
gelernten Verfahren ist:
![]()
Bei drei Zahlen gibt es
aber zwischen dem Minimum und dem Maximum noch die Zahl in der Mitte. Die
Statistiker nennen dies den Median. Nun rechnen wir damit:
![]()
Dies ist offensichtlich
die ăfehlendeŇ Zahl dazwischen.
Was soll dieses Bild?
3
Beispiel mit vier Zahlen
Wir arbeiten mit ![]() ,
, ![]() ,
, ![]() und
und ![]() .
.
3.1
kgV und ggT
Es ist:
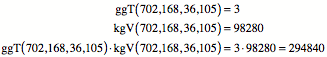
Andererseits ist:
![]()
Wir haben einen
ăfehlendenŇ Faktor:
![]()
3.2
Turnźbungen
Bei vier Zahlen gibt es
sechs mšgliche Paare. Wir rechnen paarweise das kgV:
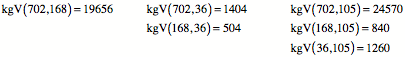
Anschlie§end berechnen
wir den ggT der sechs kgV:
![]()
Nun gehen wir umgekehrt
vor. Wir berechnen zuerst paarweise den ggT:
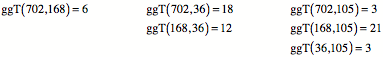
Fźr das kgV der sechs
ggT ergibt sich:
![]()
Wir erhalten zwei
verschiedene Zahlen. Das Produkt der beiden Zahlen ist aber gerade der fehlende
Faktor.
4
Hintergrund
4.1
Primfaktorzerlegungen
Wir gehen aus von n Zahlen ![]() und nehmen deren
Primfaktorzerlegung. Dabei sei m
die Nummer der grš§ten źberhaupt vorkommenden Primzahl.
und nehmen deren
Primfaktorzerlegung. Dabei sei m
die Nummer der grš§ten źberhaupt vorkommenden Primzahl.
![]()
Wir erhalten die
Exponententablle ![]() :
:
Nun ordnen wir die
Spalten der Exponententabelle der Grš§e nach, die kleinen oben. Die Elemente
der so geordneten Tabelle ![]() nennen wir
nennen wir ![]() . Es ist also:
. Es ist also:
![]()
Damit definieren wir:
![]()
Die erste Zahl, also ![]() , enthŠlt jeweils das Minimum der bei einer Primzahl vorkommenden
Exponenten. Somit ist
, enthŠlt jeweils das Minimum der bei einer Primzahl vorkommenden
Exponenten. Somit ist ![]() .
.
Entsprechend ist ![]() .
.
Auf Grund des Anordnens
der Exponenten der Primfaktoren erhalten wir die Teilerkette ![]() .
.
Da wir in den ![]() insgesamt
dieselben Primfaktoren haben wie in den
insgesamt
dieselben Primfaktoren haben wie in den ![]() , gilt:
, gilt:
![]()
Damit ist das
zahlentheoretische Problem meiner Jugend gelšst.
4.2
Beispiel
Zur Illustration nochmals
das Beispiel mit den vier Zahlen:
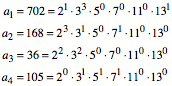
Exponententabelle:
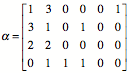
Spalten der Grš§e nach
geordnet:
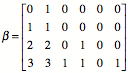
Das ergibt die Zahlen ![]() :
:
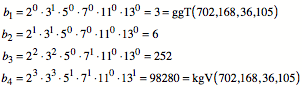
Die Zahlen 6 und 252
erhielten wir oben auch bei den Turnźbungen.
4.3
Minimax
Um von n Zahlen ![]() unter
ausschlie§licher Verwendung der beiden Funktionen min (Minimum) und max
(Maximum) zum Beispiel die drittkleinste zu finden, bestimmen wir zunŠchst von
allen Teilmengen mit genau drei Zahlen (es gibt
unter
ausschlie§licher Verwendung der beiden Funktionen min (Minimum) und max
(Maximum) zum Beispiel die drittkleinste zu finden, bestimmen wir zunŠchst von
allen Teilmengen mit genau drei Zahlen (es gibt ![]() solcher Teilmengen)
je das Maximum und anschlie§end das Minimum dieser Maxima. — Nun ja, das
ist ja wohl nicht die effizienteste Methode des Anordnens, aber lustig ist die
†berlegung allemal. — Allgemein gilt fźr die k-t-kleinste Zahl
solcher Teilmengen)
je das Maximum und anschlie§end das Minimum dieser Maxima. — Nun ja, das
ist ja wohl nicht die effizienteste Methode des Anordnens, aber lustig ist die
†berlegung allemal. — Allgemein gilt fźr die k-t-kleinste Zahl![]() :
:
![]()
Daraus ergibt sich
sofort:
![]()
Analog gilt unter
Vertauschung der Operationen:
![]()
Und entsprechend:
![]()
Nun verstehen wir auch
die Ergebnisse der Turnźbungen.